(※数式が見切れている場合は横スクロールしてください。)
さて、ここからは1次元から3次元へ抜け出すための数学準備です。マキノさん、気合いを入れていきましょう!
中学レベルの数学では、直線の方程式、放物線の方程式、双曲線の方程式(反比例)、と3種類の図形を表す方程式を習っていますね。全部かけます?
直線の方程式は
y=ax+b
\end{align}
という形で、放物線の方程式は
y=ax^2\quad(a\neq0)
\end{align}
という形で、双曲線(反比例)の方程式は
y=\frac{a}{x}\quad(a\neq0)
\end{align}
という形でしたね。思い出しました?
これらの方程式の名前が意味するところは、この関係を保った全ての\((x,y)\)という座標を\(xy\)平面にプロットすると、それぞれの名前の図形が得られるということです。
例えば、
y=\frac{1}{2}x+3
\end{align}
という関係を満たす点をxy平面にプロットすると以下のような直線が得られます。
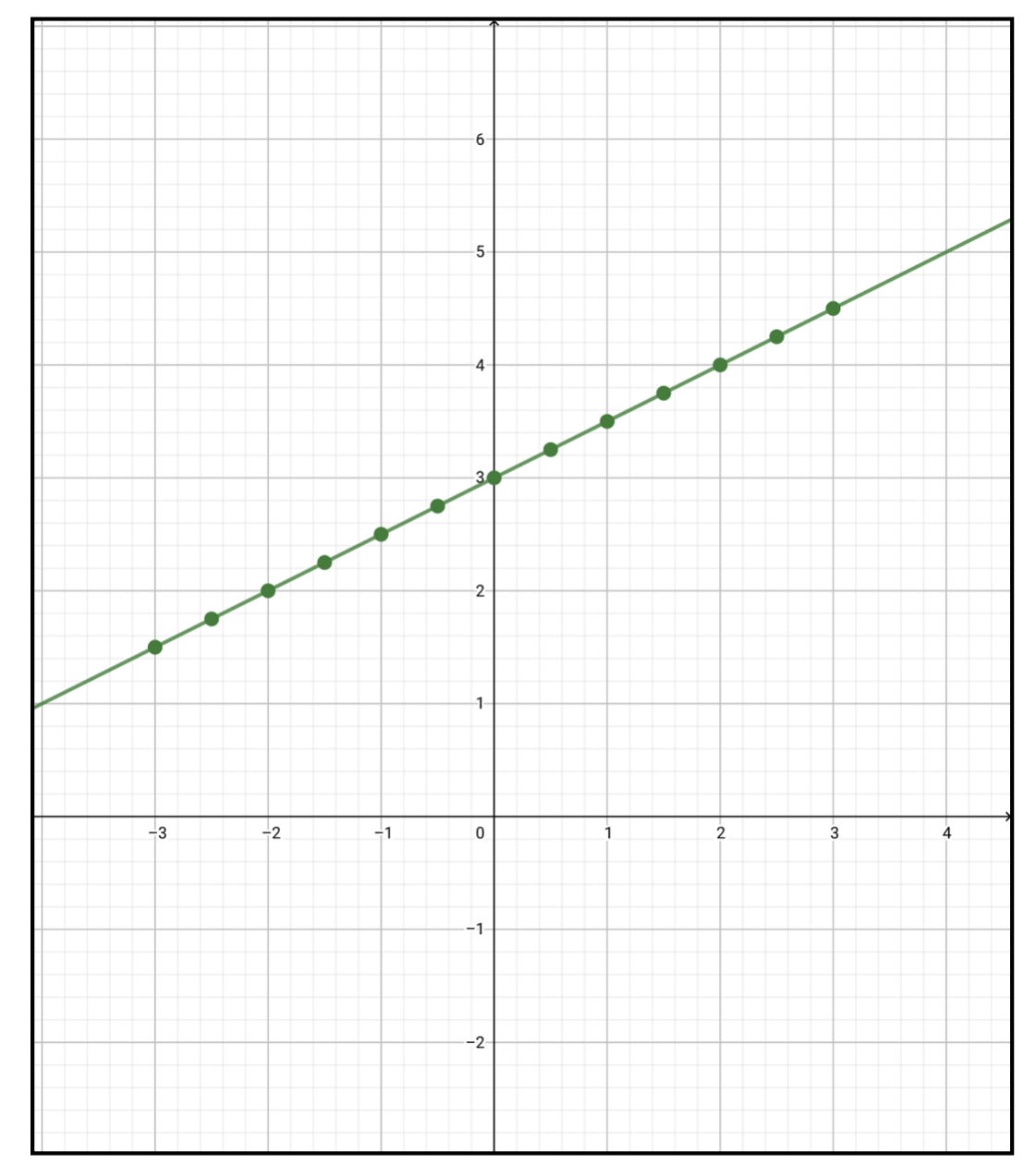
逆側から考えて、\(xy\)平面に書かれた直線上の全ての点は\((x,y)\)の間に一定の関係があって、その関係を表す式が直線の方程式である、という考え方も正しいです。
「図形の方程式」という言葉の意味が理解できましたかね?現段階では難しくてもだんだんと慣れていきますので、ひとまず先に進んでいきましょう。
この節では円の方程式というものを新たに学習します。\(xy\)平面上に円を描くような\(x\)と\(y\)の関係式を見つけて覚えるのがここでやる作業です。
\(xy\)平面上の任意の点P\((x,y)\)を準備します。点Pと原点Oの距離は三平方の定理から、
OP=\sqrt{x^2+y^2}
\end{align}
となります。
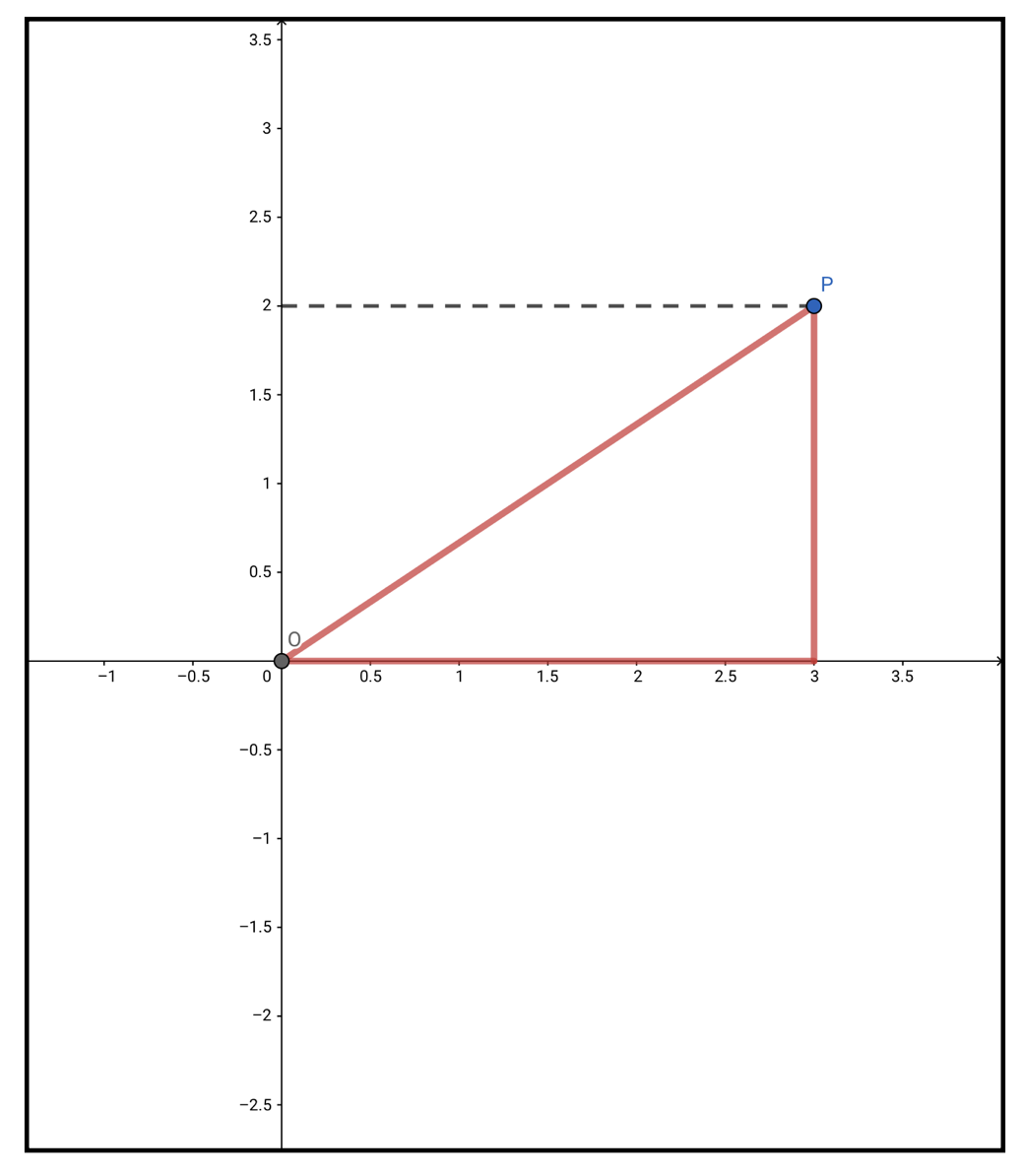
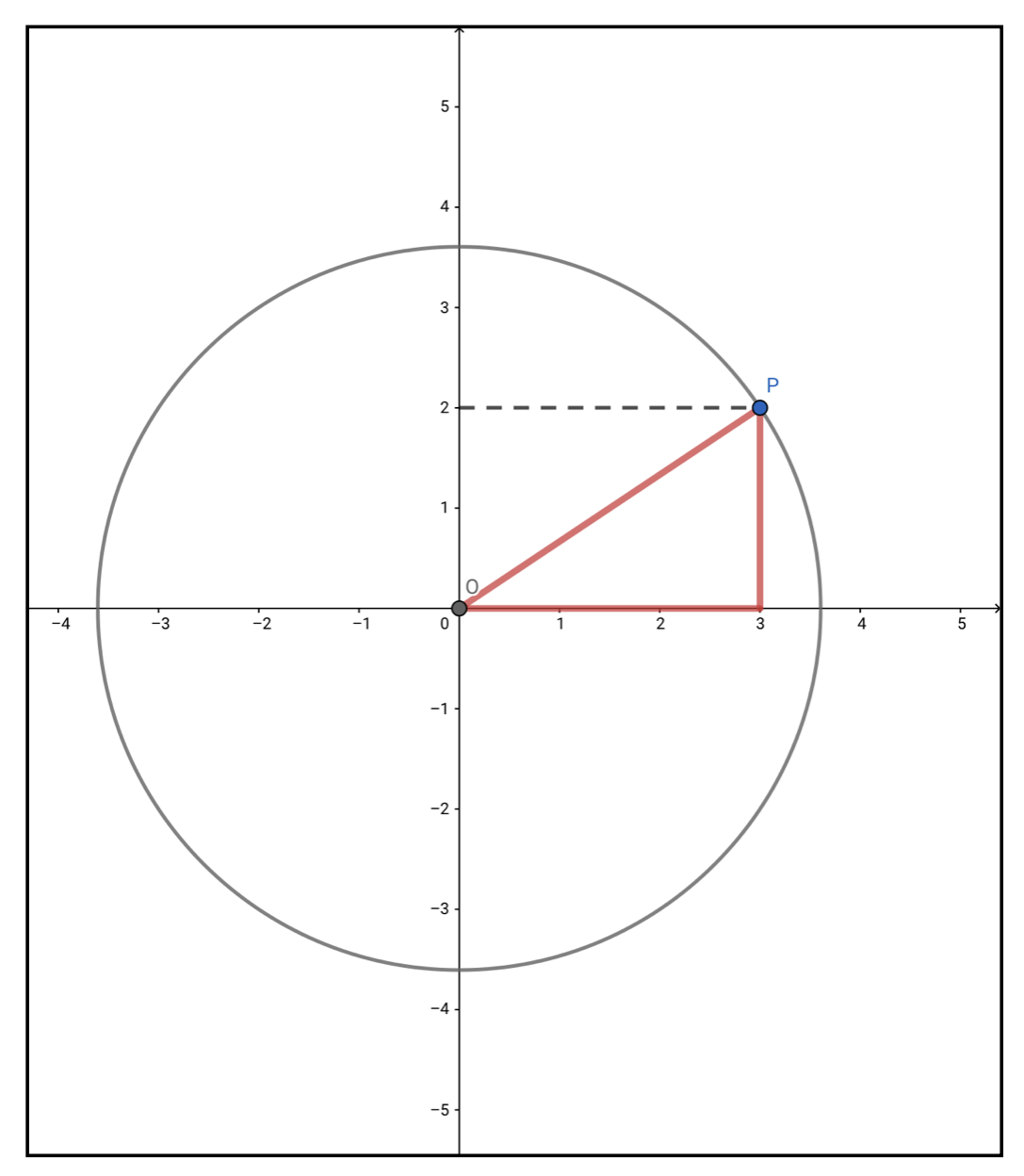
もし点Pが原点を中心とした半径\(r\)の円周上に乗っていたら、その円周上のどこに点Pが存在していても以下のような関係が成り立ちます。
&\sqrt{x^2+y^2}=r\\
\Longleftrightarrow&x^2+y^2=r^2
\end{align}
この後者の式を一般に円の方程式と呼びます。
公式
原点中心、半径\(r\)の円の方程式は以下のような形をしている。
x^2+y^2=r^2
\end{align}
問題
1. 原点中心で\((3,4)\)を通る円の方程式を求めよ。
2. 座標\((2,y)\)がその円上に存在するとき\(y\)の値を求めよ。
解答
1.
円の方程式に\((3,4)\)を代入すると
3^2+4^2=r^2\Longleftrightarrow r=5
\end{align}
から\(r=5\)がわかるのでこの円の方程式は
x^2+y^2=25
\end{align}
とわかります。
2.
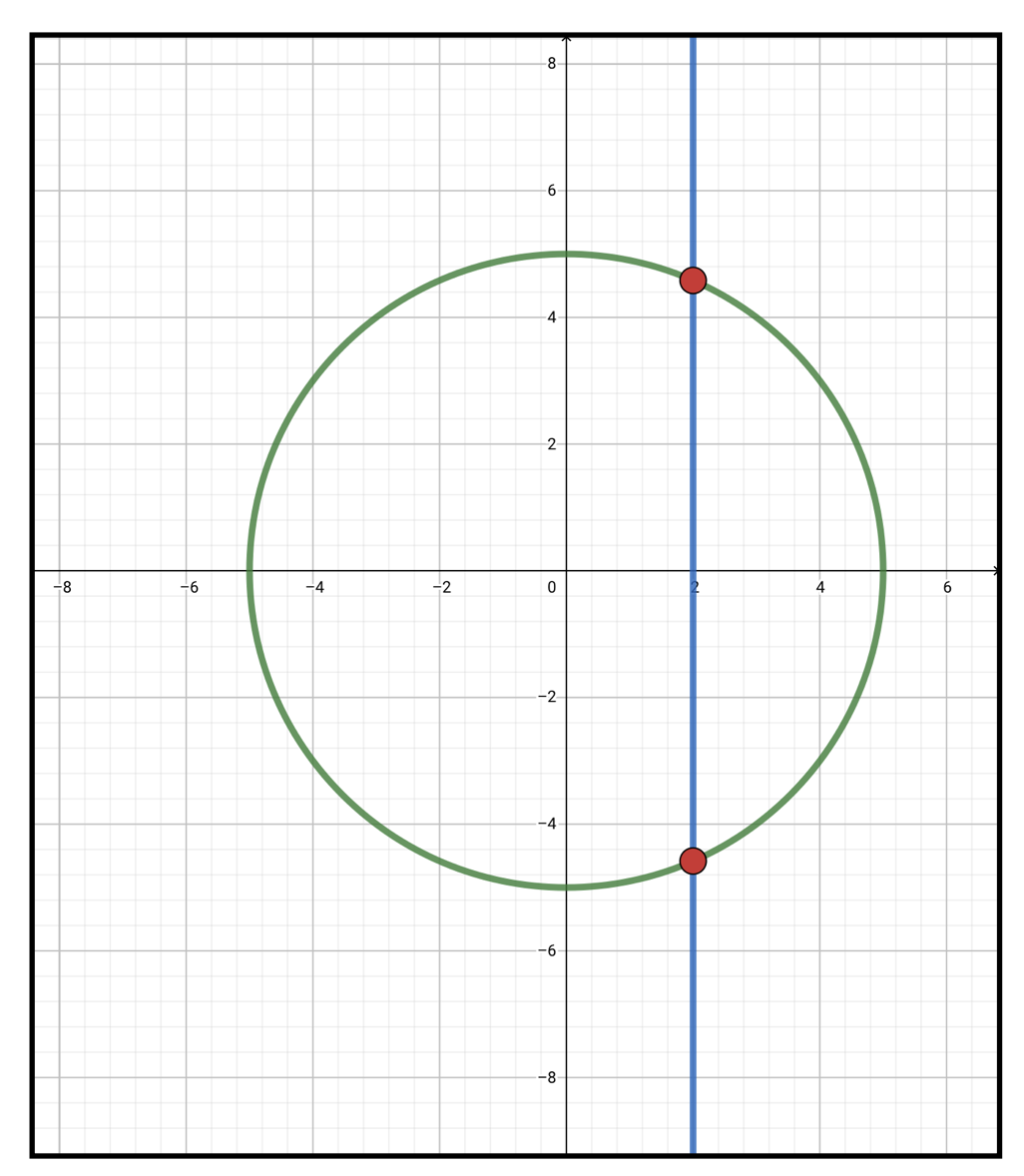
求めた円の方程式の\(x\)に\(2\)を代入すると
&2^2+y^2=25\\
\Longleftrightarrow &y^2=25-4=21\\
\Longleftrightarrow & y=\pm\sqrt{21}
\end{align}
円上に、\(x\)が\(2\)となる点が2点あるので\(y\)の値も2つあります。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」








