三角関数の極限｜ぽこラボ勉強ブログ

(※数式が見切れている場合は横スクロールしてください。)

三角関数の極限を扱う時にはただ1つの公式に着地させるのが受験的な常識なのですが、その公式自体は三角関数の微分を扱う際に重要な役割を果たすので、ここで学んでおくことにします。

まず以下の図を見てください。

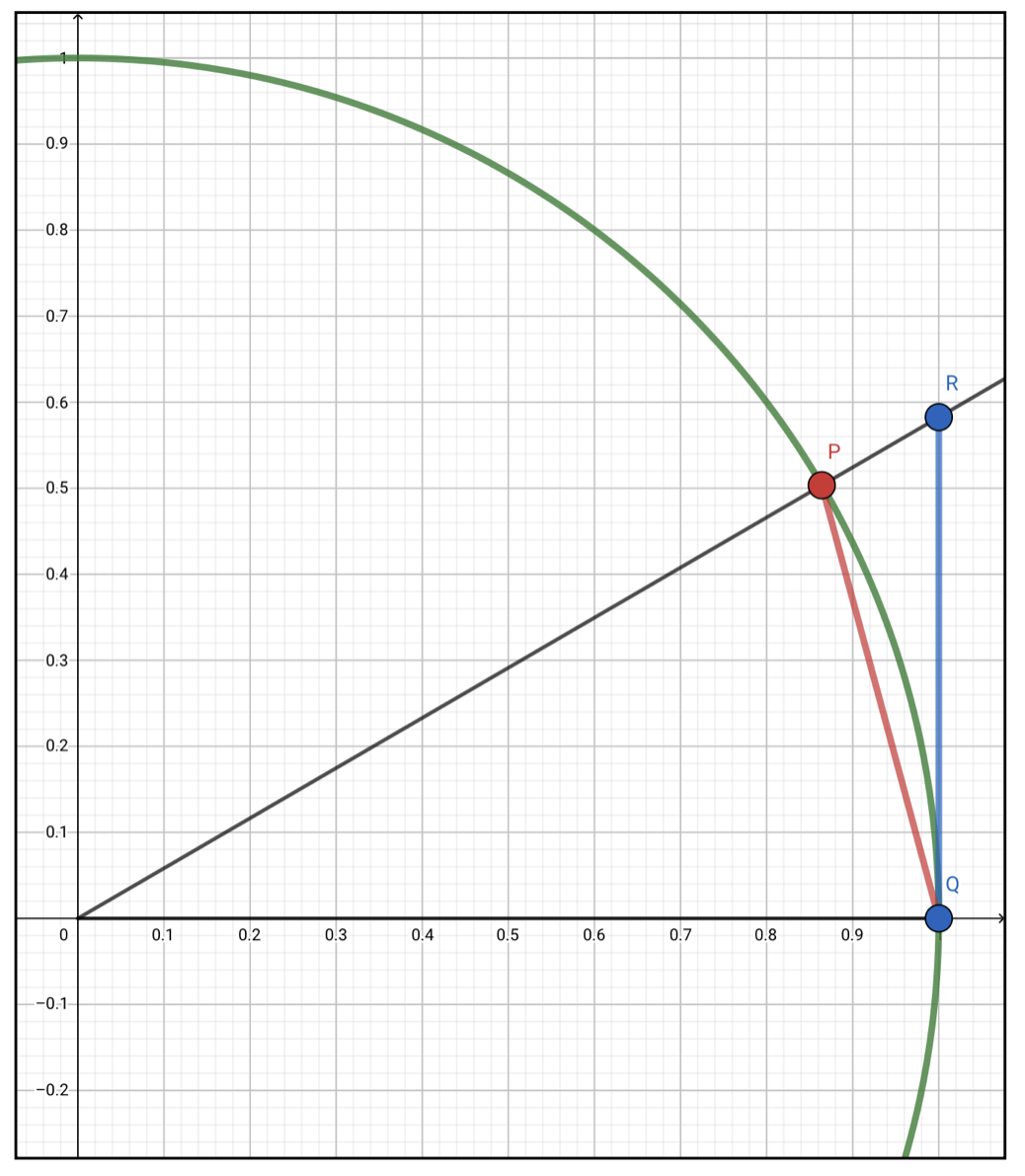
単位円上に点Pを取って、それと関連するいくつかの点を取ってきました。ここで重要なのは3つの面積の大小関係です。1つ目は三角形OPQです。これは底辺を\(1\)として高さは点Pの座標なので、

\begin{align}
OPQ=\frac{1}{2}\sin\theta
\end{align}

です。次におうぎ形OPQです。これは三角形OPQよりも明らかに大きいですよね。おうぎ形OPQの面積は

\begin{align}
\pi\times 1^2\times \frac{\theta}{2\pi}=\frac{\theta}{2}
\end{align}

となります。最後に1番大きいのが三角形ORQです。QRの長さは\(\tan\theta\)になるので、これを使うとその面積は

\begin{align}
\frac{1}{2}\tan\theta
\end{align}

とわかります。

これを不等号で繋ぐと以下のように書けますね。

\begin{align}
\frac{1}{2}\sin\theta<\frac{1}{2}\theta<\frac{1}{2}\tan\theta
\end{align}

全体を2倍して、逆数を取ってやると、以下のように書き換えられます。

\begin{align}
\frac{1}{\sin\theta}>\frac{1}{\theta}>\frac{\cos\theta}{\sin\theta}
\end{align}

逆数を取ると、不等号の向きが反転するのを忘れないようにしてください。さらに全体に、\(\sin\theta\)をかけてやります。\(\theta\)が正で小さいときには\(\sin\theta\)は正の値になるので、不等号の向きは変わりません。

\begin{align}
1>\frac{\sin\theta}{\theta}>\cos\theta
\end{align}

ここで全体を\(\theta\to 0\)の極限に持っていくことを考えましょう。この極限操作の間、先ほどの図の面積の大小関係は変わりません。またこの時、右辺の\(\cos\theta\)は\(1\)に近づいていきます。

このように不等号で両端を囲まれていて、かつある極限操作において、その両端が共にある値に近づくとき、囲まれている真ん中の値もそのある値に近づくことをはさみうちの原理と言います。

ここでは、はさみうちの原理についてとやかく言うことはありませんが、何となく感覚的に理解できますよね？今回の場合は両端が\(1\)に近づいていくんだから、\(\sin\theta/\theta\)もに近づいていくでしょってことです。

さてこの極限操作の結果は公式として覚えておくと良いでしょう。

公式

\begin{align}
\lim_{\theta\to 0}\frac{\sin\theta}{\theta}=1
\end{align}

三角関数の極限の操作を考えるときにはよく使われる公式です。

問題

次の極限を求めよ。

\begin{align}
&1.\quad \lim_{x\to 0}\frac{\sin x}{x}\\
&2.\quad \lim_{x\to \infty}\frac{\sin x}{x}\\
&3.\quad \lim_{\theta\to 0}\frac{\sin 3\theta}{\sin 2\theta}\\
&4.\quad \lim_{\theta\to 0}\frac{\sin\theta}{\tan\theta}\\
\end{align}

解答

最初の問題は公式そのものですね。

\begin{align}
\lim_{x\to 0}\frac{\sin x}{x}=1
\end{align}

この問題は公式にだまされないことが大事です。\(\sin x\)は\(\pm1\)の範囲に収まるので、それを無限で割ればゼロになります

\begin{align}
\lim_{x\to \infty}\frac{\sin x}{x}=0
\end{align}

この問題は次のように形を変えて、計算するのがコツです。

\begin{align}
&\lim_{\theta\to 0}\frac{\sin 3\theta}{\sin 2\theta}\\
=&\lim_{\theta\to 0}\frac{\sin 3\theta}{3\theta}\frac{2\theta}{\sin 2\theta}\frac{3}{2}\\
=&\frac{3}{2}
\end{align}

このように変形すれば、公式を2発使う形で問題なく計算できます。

最後は三角関数の公式を使うだけです。

\begin{align}
&\lim_{\theta\to 0}\frac{\sin\theta}{\tan\theta}\\
=&\lim_{\theta\to 0}\cos\theta=1
\end{align}

公式を新たに覚えてもそれを毎回使うとは限りません。使い所がどこかを判断できるようになるのが、これからの学習には必要になってきます。

関連リンク

>>ブログ版アラサー高校物理の記事一覧

>>物理の勉強ロードマップ【2019年版】

>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」