ども、所長です！
先日Twitterでこういった質問をいただきました。
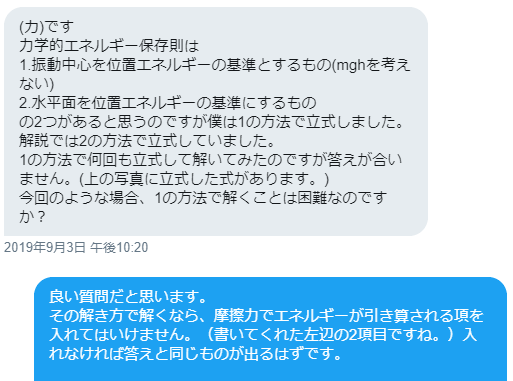
（※DMではその問題に関することだけ解説しました。）
これだけご覧になっても何のことか分からない方もいらっしゃるかもしれませんが、質問のメイントピックは以下の内容です。
これを受けて今回はこの疑問にお答えするための記事を作りました。
目次
まずは例で使い方を覚える
まずは2つほど基本的な例を挙げて2つの解き方を考えてみましょう。
重力とばねの弾性力による単振動を例に基本的な使い方を解説
一番、基本的なケースをご紹介します。
天井にばね定数\(k\)のばねを固定して、逆の端には質量\(m\)の質点をくっつけます。ばねも質点も鉛直方向にしか運動をしないとしますね。
図のように最初は静止していたとしましょう。このとき、ばねは自然長から\(d_0\)だけ伸びています。
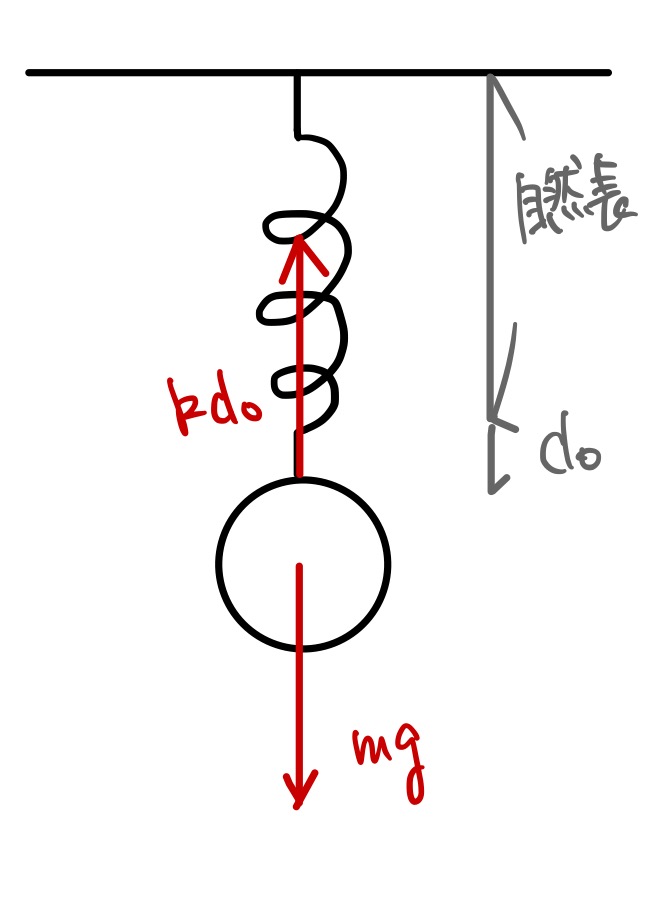
次に、この質点を長さ\(d\)だけ下向きに引っ張って離すと質点は単振動を始めます。
単振動のある瞬間に、ばねの伸びは\(x\)となりました。このときの質点の速さがいくらになるかは力学的エネルギーの保存則で解くことができます。
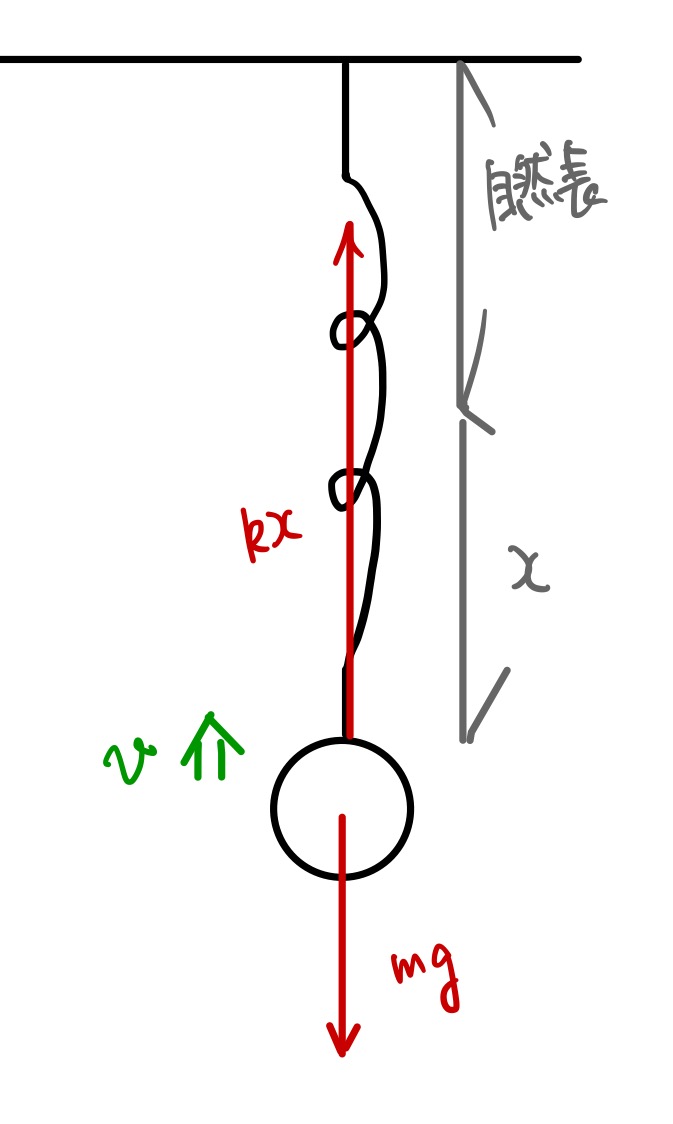
これを2種類の力学的エネルギーの保存則の立式を用いて解いてみましょう。
自然長を重力の位置エネルギーの基準と考えて解く方法
まず最初は自然長を位置エネルギーの基準としましょう。
※ちなみに基準はどこでもいいです。例えば、質点から手を離した瞬間（すなわち質点の最下点）とかでもOKです。ポイントは位置エネルギーを考慮するということ。
手を離した瞬間は速度が\(0\)で、ばねの伸びが\(d\)なので、ばねが持っている弾性エネルギーは\(kd^2/2\)です。
同時に、その瞬間は自然長の位置から下方に\(d\)だけ変位した位置に質点があるので、重力による位置エネルギーは\(-mgd\)です。
なので、この瞬間の力学的エネルギーは
\frac{kd^2}{2}-mgd
\end{align}
となります。
次に、ばねの伸びが\(x\)のときには、弾性エネルギーが\(kx^2/2\)で、その瞬間は位置エネルギーの基準の位置から\(x\)だけ下方にいるので、重力の位置エネルギーは\(-mgx\)です。
さらに運動エネルギーも考慮すると、この瞬間の力学的エネルギーは
\frac{kx^2}{2}-mgx+\frac{mv^2}{2}
\end{align}
となります。この方法だと力学的エネルギーの保存則は以下のように書けますね。
&\frac{kd^2}{2}-mgd
=\frac{kx^2}{2}-mgx+\frac{mv^2}{2}
\end{align}
あとは、\(v\)について解いてやれば、問題は解けたことになります。
※解きたい方は解いておいてください。
単振動の中心を「弾性力+重力」の位置エネルギーを単振動の位置エネルギーとする方法
今度は「弾性力＋重力」の位置エネルギーを合わせてやって、単振動の中心から計るというやり方で考えてみます。
単振動の中心はつり合いの位置になりますから、今回の場合は
kd_0=mg\Longleftrightarrow d_0=\frac{mg}{k}
\end{align}
が中心の位置になります。
ここを「重力＋弾性力」の位置エネルギーを合わせた単振動の位置エネルギーの基準点として考えるというわけです。
そうすると、重力の位置エネルギーを考慮しなくても良くなるというのがこの解き方のおいしい所です。
手を離した瞬間、運動エネルギーは\(0\)で、単振動の位置エネルギーは、
\frac{k}{2}(d-d_0)^2=\frac{k}{2}\left(d-\frac{mg}{k}\right)^2
\end{align}
です。
そして、ばねの伸びが\(x\)のときには、単振動の位置エネルギーが
\frac{k}{2}(x-d_0)^2=\frac{k}{2}\left(x-\frac{mg}{k}\right)^2
\end{align}
となります。運動エネルギーも考慮して、力学的エネルギーの保存則を書くと以下のようになります。
\frac{k}{2}\left(d-\frac{mg}{k}\right)^2=\frac{k}{2}\left(x-\frac{mg}{k}\right)^2+\frac{mv^2}{2}
\end{align}
2乗になっている所を展開したら、先ほどの力学的エネルギーの保存の式と全く同じものになることがわかります。
※こういう所でちゃんと展開して自分の力で確認してみない人がおおむね受験で失敗します。
ちなみにどっちを使って解いてくれても構いません。同じ式になるんだから、同じ答えがでますので。
少しイレギュラーな動摩擦力とばねの弾性力による単振動の例を解説
実は冒頭に取り上げたTwitterでのやり取りはこの類の問題についての質問でした。
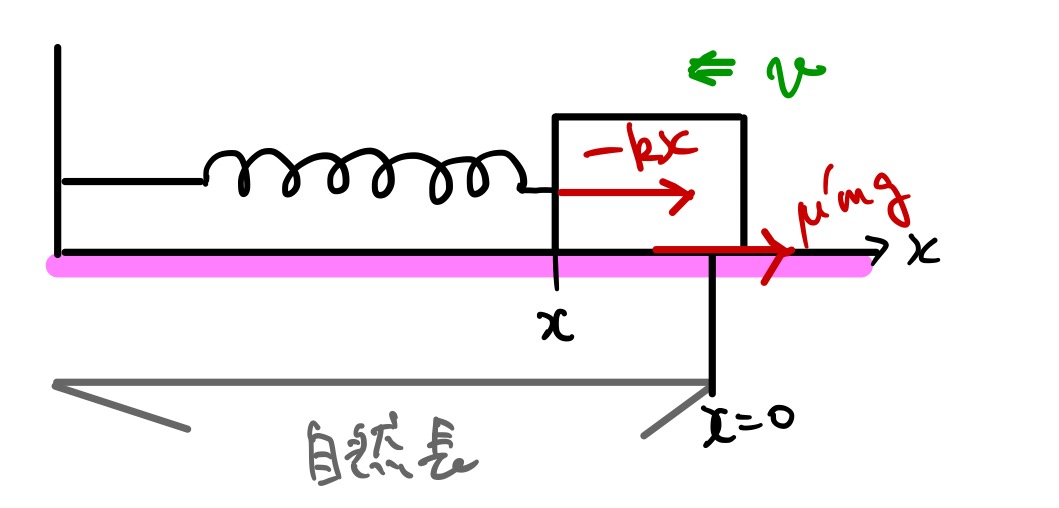
こんな例を考えてみましょう。水平面にばね（ばね定数\(k\)）にくっつけた箱（質量\(m\)）をおきます。
箱と床面との動摩擦係数は\(\mu’\)で、ばねは最初、自然長から\(d\)だけ伸ばした長さで壁に固定されています。
この状態から手を離すと、箱は単振動を始めます。
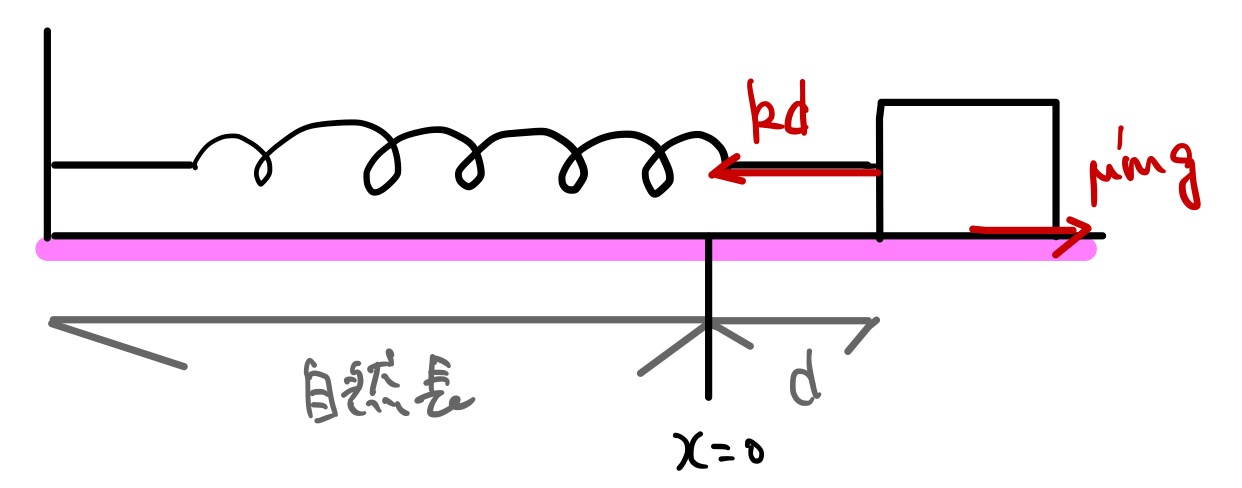
単振動と言っても、左から右に進むときと、右から左に進むときで、動摩擦の向きが変わるので、振動の中心は動摩擦の向きが変わるたびに変わります。
ここでは、手を離した瞬間から箱が初めて止まる瞬間までを考えることにしましょう。
今回は自然長の位置を\(x=0\)として、右向きに正に\(x\)軸をとりましょう。
ある位置\(x\)に来たときの箱の速度を求めるという問題を解いていく方法を2種類の方法で考えます。
自然長を位置エネルギーの基準にする方法
先ほどと同じように考えていきます。
手を離した瞬間は速度が\(0\)なので、弾性エネルギーだけが力学的エネルギーになっています。
\frac{kd^2}{2}
\end{align}
箱が\(x\)の位置に来たときには弾性エネルギーが\(kx^2/2\)で、運動エネルギーが\(mv^2/2\)なので、
\frac{kx^2}{2}+\frac{mv^2}{2}
\end{align}
だけの力学的エネルギーを持っています。ただし、この2つの力学的エネルギーは等しいわけではありません。
なぜなら動摩擦が仕事をしているからですね。それも考慮してエネルギー保存則を作ると以下のようになります。
\frac{kd^2}{2}-\mu’mg(d-x)=\frac{kx^2}{2}+\frac{mv^2}{2}
\end{align}
符号が少しややこしいので、図を見てちゃんと理解してくださいね。
「動摩擦力＋弾性力」による単振動のエネルギーを使って解く方法
さて、今度もつり合いの位置というのを考えてみましょう。
ただし、今回はつり合いといっても静止している位置ではありません。
なぜなら、動摩擦力は静止しているときには働きませんからね。
なので、つり合ってはいるけど、動いているという状況でのつり合いの位置を考えます。
単振動の中心\(x_0\)では、弾性力と動摩擦力がつり合っているので、
kx_0=\mu’mg\Longleftrightarrow x_0=\frac{\mu’mg}{k}
\end{align}
です。
まず、手を離した瞬間はつり合いの位置から考えると以下の単振動のエネルギーを持っています。
\frac{k}{2}(d-x_0)^2=\frac{k}{2}\left(d-\frac{\mu’mg}{k}\right)^2
\end{align}
これが最初の瞬間の力学的エネルギーです。
次に、位置\(x\)の時には、
\frac{k}{2}(x-x_0)^2+\frac{mv^2}{2}=\frac{k}{2}\left(x-\frac{\mu’mg}{k}\right)^2+\frac{mv^2}{2}
\end{align}
という力学的エネルギーを持っています。
こちらの解き方では、単振動のエネルギーの中に動摩擦力がする仕事の分が考慮されているので、そのまま前者と後者を比較してやればいいことになります。
これがよく間違えるポイントです。考慮し終わっているはずの動摩擦力の仕事の分を余計に書いてしまうわけですね。
\frac{k}{2}\left(d-\frac{\mu’mg}{k}\right)^2=\frac{k}{2}\left(x-\frac{\mu’mg}{k}\right)^2+\frac{mv^2}{2}
\end{align}
これで、1つ目の解き方の時に立てた力学的エネルギーの保存則と同じ式になっています。
よくある間違いは、今導いた式の左辺に\(-\mu’mg(d-x)\)という項を付け足してしまうという間違いです。
2種類の解き方で書き下した力学的エネルギーの保存則が同じになるかどうかちゃんとチェックしてください。
受験的な対処方法の解説
受験的に言うと「ばねの弾性力＋重力」だけ力がかかっている時のみ、単振動のエネルギーという考え方を使うのが無難です。
2つ目の例に出したような動摩擦力を考慮しなければならない問題だと割とミスする方が多いので。
どんな例でも両方の解き方がしたいという方は以下の解説を参考になさるとよろしいかと思います。
以下の解説が理解できる方ならどんな問題がきても、両方の解き方で解けるようになるはずです。
背景となる考え方の整理
次にこの問題をもっと正確に理解するために背景となる考え方の説明をしていきます。
簡単な微分方程式の説明も含んでいますので、少し発展的な内容になります。
※置換積分（数３）の知識が必要です。
力学的エネルギーの保存則を導く
まず、エネルギーの保存則を導けるようになっておくことが重要です。
力学的エネルギーの保存則は運動方程式を空間の成分で積分すると導くことができます。
簡単のために1次元上(直線の上)を運動している質量\(m\)の物体に\(F(t)\)の力がかかっている状況を考えます。
ある時刻における運動方程式は
m\frac{d}{dt}v(t)=F(t)
\end{align}
となります。加速度は速度の時間微分ですので、上のような式になります。
※この事実を知らない方はこちらの記事をお読みください。
>>位置、速度、加速度の関係1
この運動方程式の両辺を\(x(t_1)\to x(t_2)\)の積分区間で積分します。
m\int^{x(t_2)}_{x(t_1)}\frac{d}{dt}v(t)dx=\int^{x(t_2)}_{x(t_1)}F(t)dx
\end{align}
左辺は少し変形ができます。
積分変数を\(x\)から\(t\)に変えます。するとまず、積分区間が
\begin{cases}
x:x(t_1)\to x(t_2)\\
t:t_1\to t_2
\end{cases}
\end{align}
となります。微小幅は
\frac{d}{dt}x(t)=v(t) \Longleftrightarrow dx=v(t)dt
\end{align}
です。これらから、
\int^{x(t_2)}_{x(t_1)}\frac{d}{dt}v(t)dx=\int^{t_2}_{t_1}\left(\frac{d}{dt}v(t)\right)v(t)dt
\end{align}
さらに積分を進めるために以下の計算結果を用います。
\frac{d}{dt}\left(\frac{(v(t))^2}{2}\right)=\left(\frac{d}{dt}v(t)\right)v(t)
\end{align}
※合成関数の微分のテクニックです。
>>【web参考書】ブログ版アラサー高校物理【記事一覧】の数学準備#5をご覧ください。
すると、
&\int^{x(t_2)}_{x(t_1)}\frac{d}{dt}v(t)dx\\
=&\int^{t_2}_{t_1}\left(\frac{d}{dt}v(t)\right)v(t)dt\\
=&\int^{t_2}_{t_1}\frac{d}{dt}\left(\frac{(v(t))^2}{2}\right)dt\\
=&\frac{(v(t_2))^2}{2}-\frac{(v(t_1))^2}{2}
\end{align}
これをもとの式に戻すと以下のように力学的エネルギーの保存則が導けます。
\frac{m(v(t_2))^2}{2}-\frac{m(v(t_1))^2}{2}=\int^{x(t_2)}_{x(t_1)}F(t)dx
\end{align}
いやいや、これは力学的エネルギーの保存則に見えないと思う方も多いかもしれませんが、力学的エネルギーの保存則は基本的にこの形から全て導くことができます。
この式の意味するところは「物体の運動エネルギーの変化は物体に与えられた仕事で表現できる」ということです。
右辺は\(Fdx\)という微小変位するときの微小仕事を寄せ集めているので、仕事ということも感覚的に納得しておくのは重要です。
例に戻って確認してみる
ではまず最初の「ばねと重力の問題」に戻ってみましょう。
手を離した瞬間は速度が\(0\)で、ある時刻\(t\)において、質点が自然長から\(x\)伸びた位置にいて、速度が\(v\)だとしましょう。
このとき、先ほど導いた積分の形での力学的エネルギーの保存則は以下のようになります。
適当な\(x’\)を準備して、その場所にいるときにかかる力を間違わないようにしてください。
\frac{mv^2}{2}-\frac{m\cdot0^2}{2}=\int^{x}_{d}(-kx’+mg)dx’=-\frac{kx^2}{2}+\frac{kd^2}{2}+mgx-mgd
\end{align}
これは正に最初に導いた力学的エネルギーの保存則になっているのが分かりますよね。
次に右辺の積分をするときに\(x’\)を少し変数返還してみましょう。
形としては\(x’\to y=x’-\frac{mg}{k}\)です。
このとき、微小幅は変わりませんが、積分区間は変わります。
x’:d\to x\\
y:d-\frac{mg}{k}\to x-\frac{mg}{k}
\end{cases}\end{align}
すると力学的エネルギーの保存則は以下のように書けますね。
&\frac{mv^2}{2}-\frac{m\cdot0^2}{2}\\
=&\int^{x}_{d}(-kx’+mg)dx’\\
=&\int^{d-\frac{mg}{k}}_{x-\frac{mg}{k}}(-ky)dy\\
=&\frac{k}{2}\left(d-\frac{mg}{k}\right)^2-\frac{k}{2}\left(x-\frac{mg}{k}\right)^2
\end{align}
これは2番目に導いた、力学的エネルギーの保存則になっています。
被積分関数が簡単になる一方で、積分区間が面倒になるという変数変換を用いて少し変形しただけということが流れを見ると理解できると思います。
変数変換は「座標軸の取り方を変える」ということに対応しています。実際、\(x’\to y=x’-\frac{mg}{k}\)が平行移動を表しているのはここまで理解できた方なら理解できるでしょう。
そして、座標軸を取り換えることは正に「位置エネルギーの基準を取り換える」ことと同じということになりますね。
ちなみに積分の形の力学的エネルギーの保存則が使えると動摩擦力が関係あるときでもミスはほとんどしません。
なぜかというと、この形からスタートすれば、基本的には運動エネルギー以外は全て仕事として扱うことになりますので、座標変換を施そうが施しまいが、余分な仕事を足してしまうということはありません。
ただ、この積分を毎回おこなっているくらいなら、高校物理の教科書の範囲で習う力学的エネルギーの保存則を正しく用いた方が、計算にかかる時間は短くて済むことが多いということは理解しておいてください。
まとめ
今回の記事では以下のような内容を勉強しました。
- 力学的エネルギーの保存則の2種類の式の立て方が同等のものであることを2つの例を通して確認
- 受験的には「重力＋弾性力」のとき以外は単振動のエネルギーは使わないのが無難
- 運動方程式の積分で、運動エネルギー以外を仕事として扱う力学的エネルギーの保存則を導出
- 積分の形で見ると、変数変換＝位置エネルギーの基準の取り換えが見やすい
お役に立ったなら幸いです。
以下の単振動の全種類という記事もおすすめなので、ぜひそちらもご覧ください。
それではまた、所長でした！
>>【単振動が難しいのは種類を知らないから】高校物理の単振動全7種類【アラサー高校物理特別記事】
無料で学べる高校物理の参考書はこちら。
>>【web参考書】ブログ版アラサー高校物理【記事一覧】
東大理系攻略法を
解説したPDF販売中！
中高一貫校に行かなくても、塾に行かなくても、独学で受かるための勉強法を完全解説！
全科目の参考書
全参考書の使い方
受験までの勉強スケジュール
が全てわかります！
今だけ！100様限定60%OFF！
さらに24時間以内なら返金保証つき！
無料サンプル公開！
