ども、所長です!
さて、今回は高校物理で出てくる単振動のまとめです。単振動は7種類覚えておけば、あとはそれの少し発展形が出る程度のものです。
ばねの弾性力が最も基本的ですが、それ以外の単振動も一通り勉強しておくと大学受験で単振動の問題が出てきたときにも安心して挑戦できるかと思いましたので、こちらの記事を作りました。
学校の先生なんかもぜひ活用してください。
参考資料
参考資料としては、以下の問題集や参考書を使いました。
- 物理のエッセンス
- 良問の風
- 名問の森(上巻)
※他の参考書も確認しましたが、この3冊で単振動の全てのパターンは網羅しています。
単振動の条件
こちらの記事をご覧になっている方には必要ないかもしれませんが、単振動の条件についても書いておきます。
運動方程式が基本的には以下の形をしていればOKです。
m\vec{a}(t)=-K(\vec{x}(t)-\vec{C})
\end{align}
ここで、\(\vec{a}(t)\)と\(\vec{x}(t)\)はある物体の位置と加速度を表していて、\(m\)はその物体の質量です。
(※ベクトルで書かない方が高校の範囲では自然かもしれませんので、以降の解説ではベクトルを表す→はつけません。)
\(K\)は時間に依らない定数です。
また、\(\vec{C}\)は定数ベクトルで、\(\vec{0}\)でもいいですし、そうでなくても構いません。大事なのは時間に依らないということです。
この運動方程式を満たす物体は単振動をします。
運動方程式の右辺\(-K(\vec{x}(t)-\vec{C})\)には復元力という名前がついていますね。
復元力の頭についている\(K\)と物体の質量\(m\)によって、単振動の角速度\(\omega\)が決まり、その値は
\omega=\sqrt{\frac{K}{m}}
\end{align}
です。この記事を読まれている方にとってはおそらく周期の方がなじみやすいでしょうから、角速度\(\omega\)から周期\(T\)を求めておくと以下のようになります。
T=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{m}{K}}
\end{align}
あとは初期条件(単振動が始まった時刻の物体の位置と速度)によって単振動は全て決定されますが、この辺の詳しいことは今回は置いておくことにします。
以下の解説では
- 復元力の形になるかどうか物体にかかっている力を考察し、
- その形から単振動の周期を求めてコメントがあればコメントする
という流れで様々な単振動を説明していきたいと思います。
ばねによる単振動
最初は基本的なものですね。
壁にばね定数\(k\)のばねkがくっついていて、逆側に質量\(m\)の質点mがくっついている状況を考えます。
床と質点の摩擦はなく、水平にばねと質点mが動くので、重力の影響も考えなくていい状況です。
自然長の長さになる位置を\(x=0\)として、ばねが伸びる方向を\(x\)の正の方向、縮む方向を\(x\)の負の方向とします。
このとき、ばねが単振動することを示してみましょう。
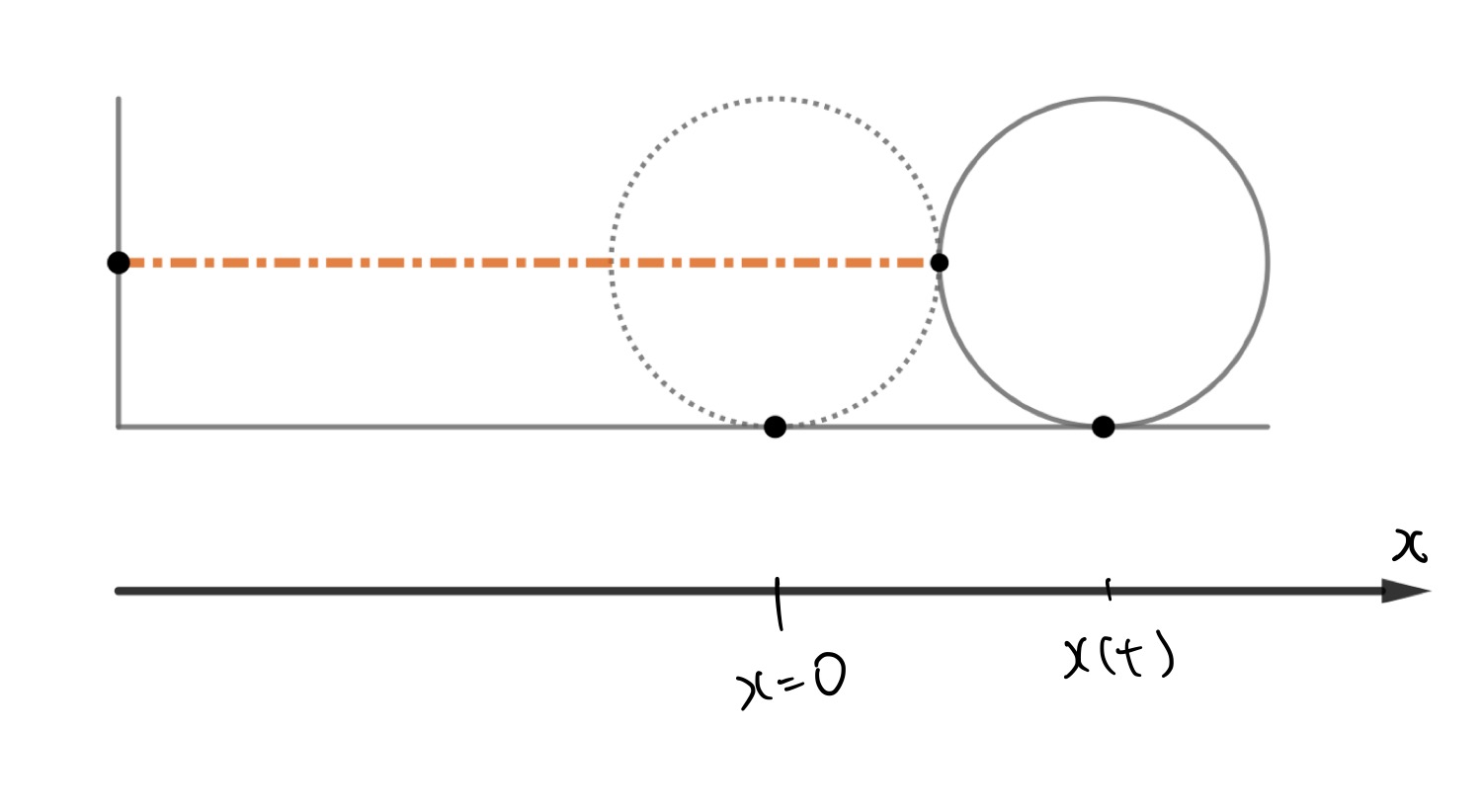
質点が\(x(t)\)という位置にいるときには、次のような力がかかります。
F(t)=-kx(t)
\end{align}
この形は復元力の形になっていますね。すぐに周期が計算できて以下のようになります。
T=2\pi\sqrt{\frac{m}{k}}
\end{align}
質点の質量\(m\)が大きいほど、周期は大きくなります。
そしてばね定数の\(k\)が大きいほど、周期は小さくなります。ばね定数\(k\)はばねの強さを表しているものと考えるといいですね。
振り子の単振動
長さ\(l\)の伸び縮みしない質量の無視できる糸の先に質量\(m\)の質点を固定し、その糸の逆の端を天井に固定したとします。
図のように少しだけ持ち上げて質点を離すと、質点が単振動することを見ておきましょう。
振り子の場合は、振動の幅が狭いということがかなり重要なので、そこは外さないようにしてください。
図のようにある角度\(\theta(t)\)になったとき、質点にかかる力は以下の図のようになります。
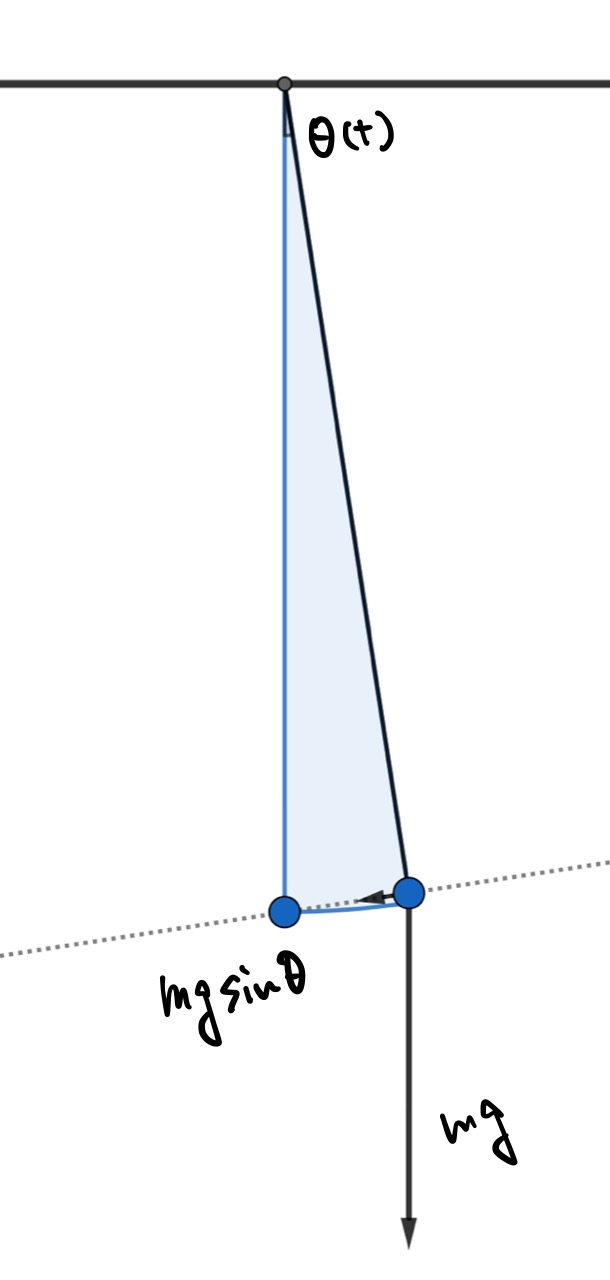
振動幅が狭いときには接線方向にかかる力\(mg\sin\theta\)が復元力となります。最下点Oから円周に沿った変異を\(x(t)\)とすると、
x(t)=l\theta(t)
\end{align}
です。角度\(\theta(t)\)が小さいとすると、\(\sin\theta\simeq \theta\)と近似できるので、
F(t)=-mg\sin\theta(t)\simeq -mg\theta(t)=-\frac{mg}{l}x(t)
\end{align}
と書けます。これは復元力の形になっていますね。
周期は
T=2\pi\sqrt{\frac{l}{g}}
\end{align}
です。\(g\)は定数とみると、この単振動は糸の長さ\(l\)によって周期が決まるということですね。
糸が長いほど周期が長くなります。
浮力による単振動
長さ\(l\)、底面積\(S\)、密度\(\rho\)の円柱を、
密度\(\rho_w\)の水に浮かべている状況を考えましょう。
重力加速度は\(g\)で、円柱は鉛直方向にしか動けないとします。
浮かべて十分な時間が経つと、円柱の\(l_0\)の長さの部分だけが水に沈み、静止しました。
その静止状態から、少しだけ円柱を下方に沈めて、手を離すと円柱は単振動をし始めることを見てみましょう。
まず静止しているとき、重力と浮力がつりあっているので、以下のような式が書けますね。
l S\rho g=l_0 S\rho_w g
\end{align}
その位置を\(x\)軸の原点として、そこから下方向を正の向きとします。
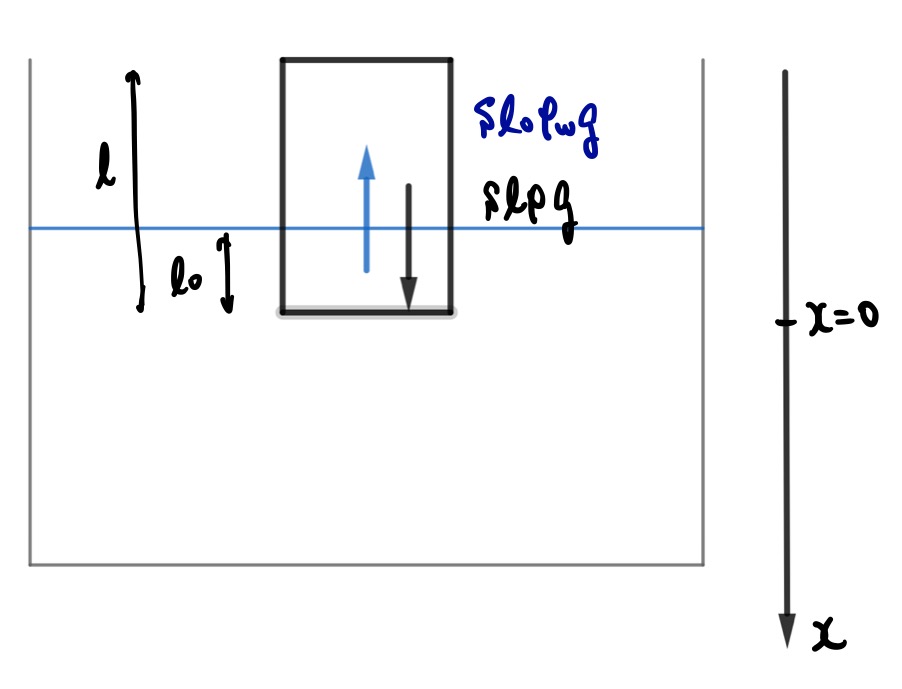
ふたの底が\(x\)の位置にあるときには円柱にかかる合力は以下のようになります。
l S\rho g-(l_0+x) S\rho_w g=-S\rho_w g x
\end{align}
これは復元力の形になっていますね。円柱の質量が\(l S\rho\)であることに注意すると、周期は以下のようになります。
T=2\pi\sqrt{\frac{l S\rho}{S\rho_w g}}=2\pi\sqrt{\frac{l \rho}{\rho_w g}}
\end{align}
底面積の大きさには関係がなく、\(\rho/\rho_w\)という密度の比と円柱の長さによって周期が決まるということがわかります。
気体による単振動
底面積\(S\)のピストンを水平方向に置きます。
ふたの質量は\(m\)です。
大気圧は\(p_0\)、外気温は\(T_0\)とします。
この実験の最中にピストン内部の気体の気温は変化しないとしましょう。
最初、ピストン内部の気圧は大気圧と等しく、ピストンのふた部分は静止していたとします。
ここでもやはり、ふたを少しだけ奥に押し込んで、手を離すとふたが単振動することを見ることにします。ただし、この単振動も微小な振幅の振動であることが条件として必要です。
最初の状態で、ピストンの内部に\(n\)molの気体が入っていて、それが理想気体(※高校物理ではほとんど理想気体しか扱いませんが。)で、気体定数を\(R\)としましょう。
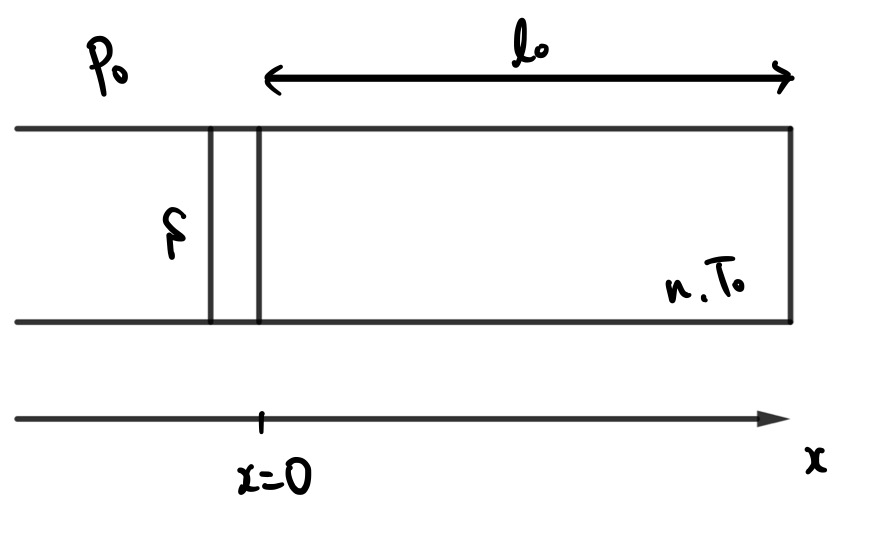
さらに\(l_0\times S\)を最初の状態のピストン内部の気体の体積とすると、最初の状態での理想気体の状態方程式は
P_0 l_0S= nRT_0
\end{align}
です。最初のふたの位置を\(x=0\)として、ふたが押し込まれる方向を\(x\)の正の方向とします。
動き始めたあと、ふたが\(x(t)\)の位置にいるとすると、このときのピストン内部の気体の状態方程式は
P(x) (l_0+x(t))S= nRT_0
\end{align}
ここで\(P(x)\)はふたの位置が\(x(t)\)のときの内部の気体の圧力です。最初の状態方程式と比べると、
&P(x) (l_0+x(t))S=P_0 l_0S\\
\Longleftrightarrow
&P(x)=\left(1+\frac{x(t)}{l_0}\right)^{-1}P_0
\end{align}
となります。ここで、\(x(t)/l_0\)が\(1\)に比べて十分小さいとき、
&P(x)=\left(1+\frac{x(t)}{l_0}\right)^{-1}P_0\simeq \left(1-\frac{1}{l_0}x(t)\right)P_0
\end{align}
と近似できます。
このとき、ふたにかかる力は以下のようになります。
P(x)S-P_0S\simeq -\frac{P_0S}{l_0}x(t)
\end{align}
この形は正に復元力の形ですね。この形からすぐに単振動の周期が分かります。
T=2\pi\sqrt{\frac{ml_0}{P_0S}}
\end{align}
今回は\(P_0S\)という大気圧による力と\(l_0\)というピストンの長さの比がばね定数と同じ役割をするということが分かります。
万有引力による単振動
密度が\(\rho\)で一定で半径が\(R\)の惑星の中に図のように穴をあけたとします。
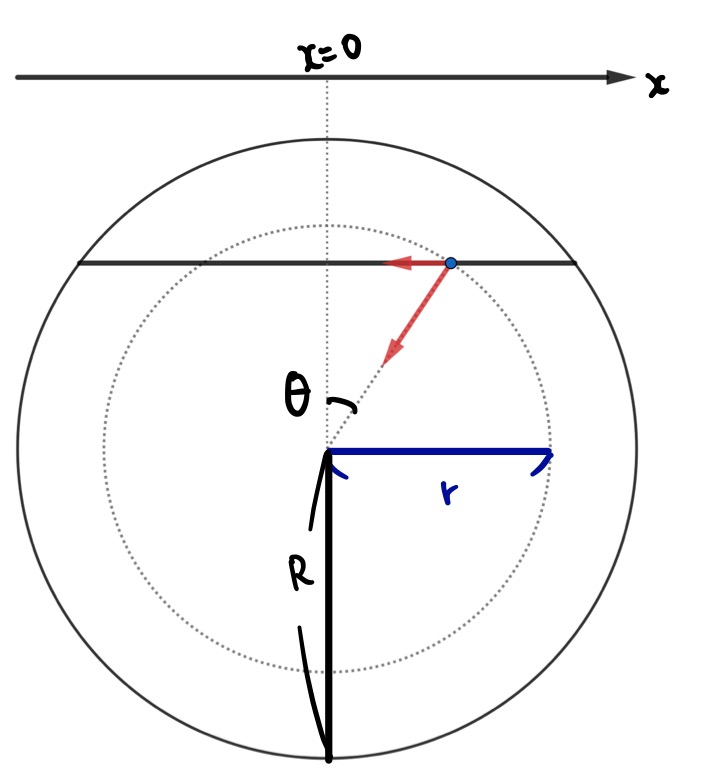
そこに質量\(m\)の質点を入れてみると単振動し始めることを見ることにします。
この実験の最中は万有引力以外の力は考えないことにします。万有引力定数は\(G\)とします。
万有引力版のガウスの法則のようなものも本当は真面目に証明した方が良いんですけど、本筋から外れてしまうので、以下のルールは知っていることにしますね。
質点にかかる惑星からの万有引力の大きさは、質点よりも内側にある惑星の質量が、惑星の中心にあるものとして、計算したものと等しい。
ちょっとややこしいんですけど、まあよく出てくる話なので、覚えておいて損はないと思います。
アラサー高校物理のテキスト内でももうすぐ書く予定です。
図のように\(x\)軸を取って、図のとき、質点が\(x(t)\)にいるとします。このとき、惑星のうち、質点よりも内側の体積は\(4\pi r^3/3\)なので、万有引力の大きさは
\left|F\right|=G\frac{\rho\frac{4\pi r^3}{3}m}{r^2}=G\frac{4\pi r\rho m}{3}
\end{align}
このうち、\(x\)方向の成分は\(x/r\)倍して、マイナスを付けたものになるので、質点にかかる\(x\)方向の成分は以下のようになります。
-G\frac{4\pi r\rho m}{3}\times \frac{x}{r}=-G\frac{4\pi \rho m}{3}x
\end{align}
これで復元力の形になっていることになります。惑星にトンネルを掘ると、そこに飛び込んだものは単振動するということですね。
(※実際には丈夫な物質を放り込んでも密度が一定でないだろうから、そんなに簡単には説明できないです。)
単振動の周期は
T=2\pi\sqrt{\frac{3m}{4\pi \rho mG}}=2\pi\sqrt{\frac{3}{4\pi \rho G}}
\end{align}
質点の質量には関係ない値になることがわかりますね。
\(G\)は定数なので、周期は惑星の密度によって決まるということです。
摩擦による単振動
内向きに回転する2つの円柱の上に、質量\(m\)の厚さを無視できる板を乗せます。円柱の間の距離は\(d\)とします。
以下の図のように板の重心が2つの円柱のど真ん中から右に\(x(t)\)にずれている時に板にかかる力を考えればいいことになります。
動摩擦係数は\(\mu’\)、重力加速度は\(g\)とします。
このとき、図のように垂直抗力と動摩擦力を置いて考察を進めます。
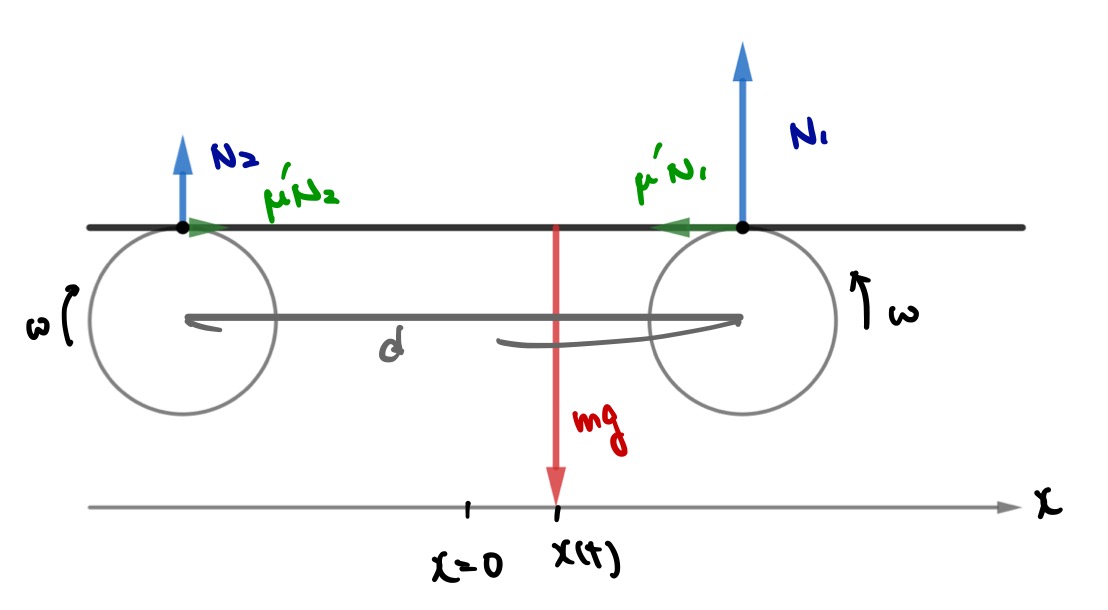
板にかかる合力を求めるためには、鉛直方向のつり合いの条件と、回転しないという条件の2つが必要です。
\begin{cases}
mg=N_1+N_2\\
\left(\frac{d}{2}-x(t)\right)mg=dN_2
\end{cases}
\end{align}
ここから、
N_1=\left(\frac{1}{2}+\frac{x(t)}{d}\right)mg\\
N_2=\left(\frac{1}{2}-\frac{x(t)}{d}\right)mg
\end{align}
が分かります。よって、板にかかる水平方向の合力は以下のようになります。
\mu’N_2-\mu’N_1=-\mu’\cdot 2\frac{mg}{d}x(t)=-\frac{2\mu’mg}{d}x(t)
\end{align}
これは復元力の形ですから、板は単振動をすることがわかります。
そして、その単振動の周期は
T=2\pi\sqrt{\frac{dm}{2\mu’mg}}=2\pi\sqrt{\frac{d}{2\mu’g}}
\end{align}
です。板の長さと、動摩擦係数によって単振動の周期が決まるということがわかります。
U字管の中の液体の単振動
最後はU字管の中の密度\(\rho\)液体の単振動です。
以下の図のようにU字管の中に液体を貯めて、そこに質量の無視できるふたをつけます。
U字管の断面積は\(S\)でどの部分でも一定とします。
重力加速度は\(g\)です。
U字管の中に入っている液体の全体の長さは\(l\)とします。
液体とふたをセットして十分に時間が経つと、2つのふたは同じ高さの所で静止します。
ここから片方のふたを押し込んでみると、単振動を始めます。
図のように高さの差の分だけ余分に重力がかかります。他の部分にかかる重力と大気圧から来る力はキャンセルされます。
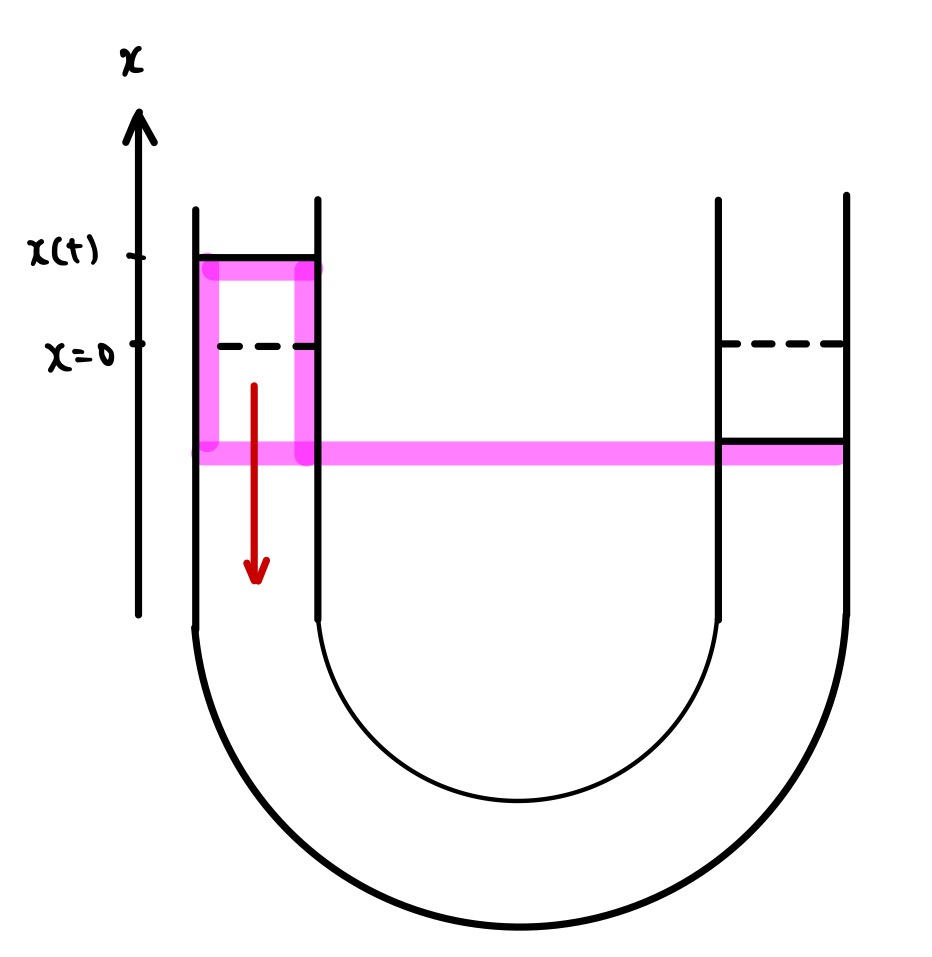
結局、液体全体にかかる合力は
-S\rho g \cdot 2x(t)=-2S\rho g x(t)
\end{align}
となります。ここで、液体全体の質量が\(Sl\rho\)であることに注意すると、以下のように単振動の周期を求められます。
T=2\pi\sqrt{\frac{Sl\rho}{2S\rho g}}=2\pi\sqrt{\frac{l}{2 g}}
\end{align}
かなり振り子と似たような形になりましたね。液体部分の長さによって単振動の周期が決まるということです。
まとめ
今回はアラサー高校物理特別記事の第一弾として、高校物理で出てくる単振動の種類を一通りまとめてみました。
意外にこういったまとめがされている参考書とか問題集ってないんですよね。
今回は基本的な形のみを書きましたから、あなたが出会うときには、これらの単振動の発展形であることが多いです。
しかし、単振動の形になる可能性があるかもなと思って、問題に取り組めるかどうかで問題に対する意気込みは変わってくるはずですので、ここで出てきているものは、あなたの手で一通り、導けるようになっておくことをおすすめします。
興味があれば以下の記事もお読みください。
それではまた、所長でした!
>>2種類の力学的エネルギーの保存則の違いがわからない方へ【アラサー高校物理特別記事】
無料で学べる高校物理の参考書はこちら。
>>【web参考書】ブログ版アラサー高校物理【記事一覧】
物理の参考書や教材の使用順序に迷ったらこちら。
>>物理の勉強ロードマップ【2019年版】








