(※数式が見切れている場合は横スクロールしてください。)
もういちど、少しだけ数学の勉強をしてから、また物理に戻ることにします。ここまでの数学がわかっていればそれほど難しくないはずです。
ベクトルはここまで図形的な処理をしていましたが、グラフ上にベクトルを書いて、もう少し、数式的な処理をすることができます。
これまでに習ったように、力や速度などなどはベクトルで表現されますし、それを微分したり、積分したりして、運動方程式を解くなどなどの操作をしなければならないわけですから、少なくとも時間依存するベクトルの時間微分や時間積分が必要なことはこれまでの議論から想像がつきますよね。
というわけで、そういったものの準備をしていきます。
まずベクトルは座標平面や空間において成分表示することができるということからはじめます。たとえば以下のようにベクトルを成分表示したとき、
\vec{a}=\begin{pmatrix}2\\1\end{pmatrix}
\end{align}
対応するベクトルの図は以下のようなものになります。
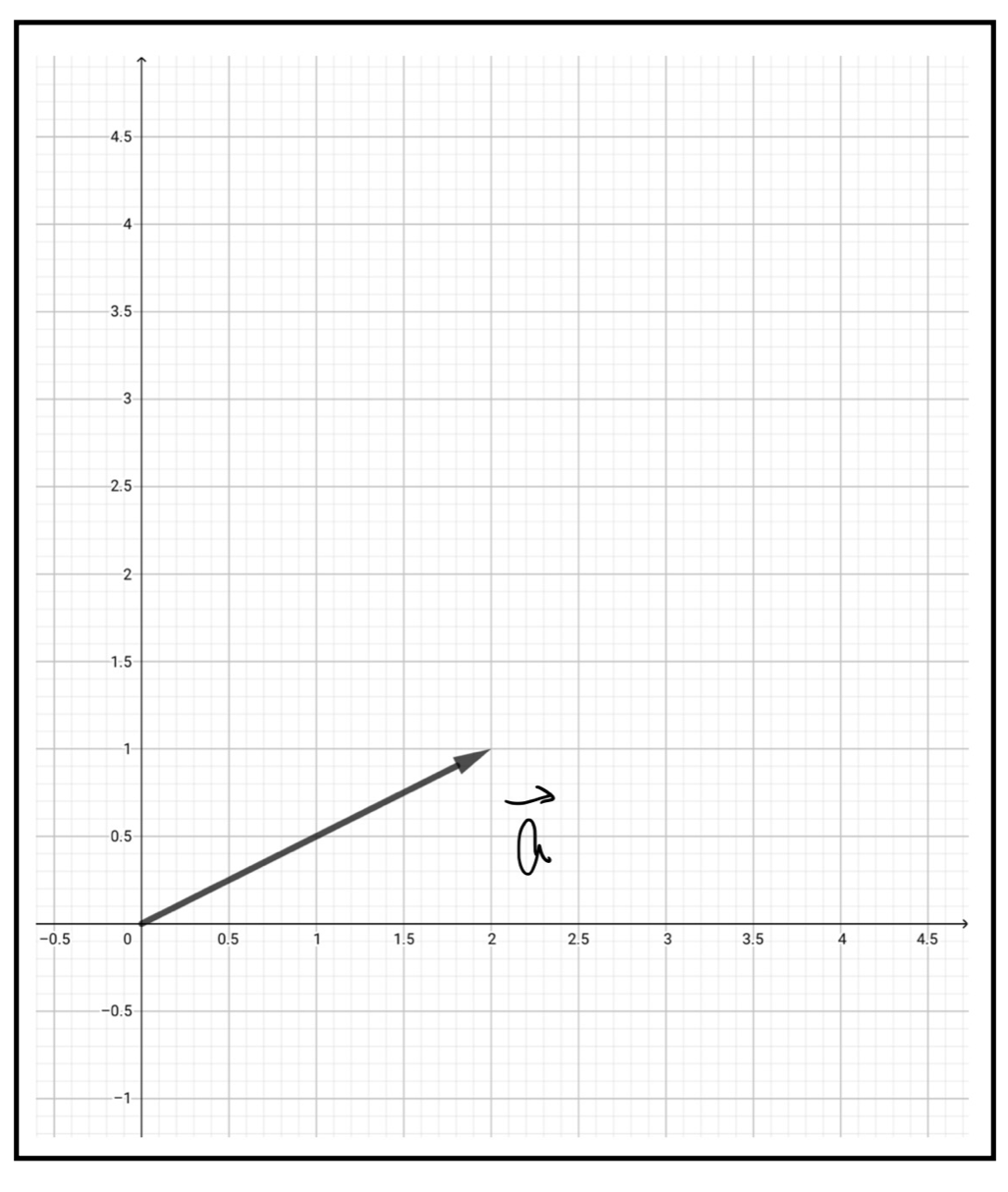
別に大したことはないですよね?中学校で習う座標の書き方を縦書きにしただけみたいな感じです。ここから先は、何も指定をしないときには、2成分のベクトル(縦にふたつの数字が並ぶベクトル)なら、上から\(x\)成分、\(y\)成分とし、3成分ベクトルなら、上から\(x\)成分、\(y\)成分、\(z\)成分とします。「成分」の数と次元の数が対応していると思っておいてください。
成分表示したベクトルもこれまで習ったように合成することができます。
例えば次の2つのベクトルの合成を考えてみましょう。
\vec{a}+\vec{b}=\begin{pmatrix}2\\1\end{pmatrix}+\begin{pmatrix}1\\2\end{pmatrix}=\begin{pmatrix}3\\3\end{pmatrix}
\end{align}
この式から分かるように、\(x\)成分は\(x\)成分同士、\(y\)成分は\(y\)成分同士で足し算すれば、合成の図形的な性質も以下のようにこれまで習ったものと同じになります。
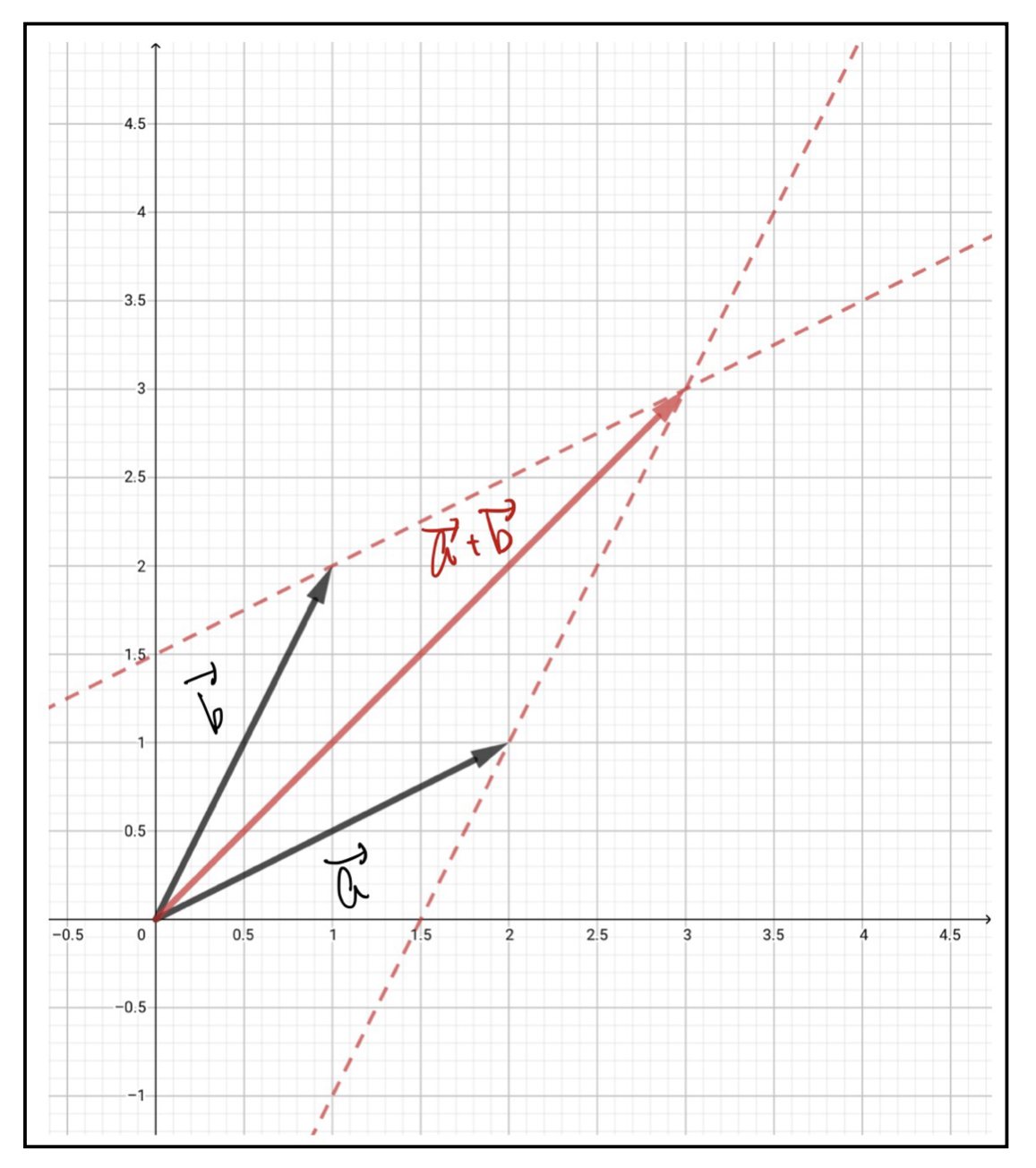
一応、成分表示の足し算について、定義を書いておくので、これを理解して覚えておいてください。
定義
以下のふたつのベクトル
\vec{a}=\begin{pmatrix}a_x\\a_y\end{pmatrix},\quad\vec{b}=\begin{pmatrix}b_x\\b_y\end{pmatrix}
\end{align}
と定数\(A\)、\(B\)が与えられたとき、以下のように計算できる。
&A\vec{a}+B\vec{b}\\
=&A\begin{pmatrix}a_x\\a_y\end{pmatrix}+B\begin{pmatrix}b_x\\b_y\end{pmatrix}\\
=&\begin{pmatrix}Aa_x+Bb_x\\Aa_y+Bb_y\end{pmatrix}
\end{align}
また3成分でも4成分でも同様に計算できる。
問題
以下の二つのベクトルが与えられているとき、次の計算をせよ。
\vec{a}=\begin{pmatrix}1\\2\\3\end{pmatrix},\quad\vec{b}=\begin{pmatrix}3\\2\\1\end{pmatrix}
\end{align}
&1.\quad 2\vec{a}-\vec{b}\\
&2.\quad-\vec{a}+3\vec{b}
\end{align}
解答
1.
&2\vec{a}-\vec{b}\\
=&2\begin{pmatrix}1\\2\\3\end{pmatrix}-\begin{pmatrix}3\\2\\1\end{pmatrix}\\
=&\begin{pmatrix}2-3\\4-2\\6-1\end{pmatrix}=\begin{pmatrix}-1\\2\\5\end{pmatrix}
\end{align}
2.
&2\vec{a}-\vec{b}\\
=&\begin{pmatrix}-1+9\\-2+6\\-3+3\end{pmatrix}=\begin{pmatrix}8\\4\\0\end{pmatrix}
\end{align}
成分表示ついでにベクトルの大きさについて言及しておきます。
座標平面上で、点と点の距離を知ろうと思ったら、三平方の定理を使っていました。それと同じ要領でベクトルの大きさを計算することができます。
例えば、先程のこちらの図に着目してみましょう。

\(\vec{a}\)や\(\vec{b}\)の大きさは三平方の定理から即座に計算ができて、以下のようになります。
\left|\vec{a}\right|=\sqrt{2^2+1^2}=\sqrt{5}\\
\left|\vec{b}\right|=\sqrt{1^2+2^2}=\sqrt{5}
\end{align}
ここで、ベクトルの大きさという意味を表すときに縦棒2本でベクトルを挟む表現を使いました。以降、この表現はベクトルの大きさを表すときに多用します。
同じように\(\vec{a}+\vec{b}\)の大きさも以下のように計算できます。
\left|\vec{a}+\vec{b}\right|=\sqrt{3^2+3^2}=3\sqrt{2}
\end{align}
より便利な考え方として、ベクトルの大きさを計算する際には以下のような定義を使うと覚えておくといいですね。
定義
\(\vec{a}\)を以下のように与えるとき、
\vec{a}=\begin{pmatrix}a_1\\a_2\\\cdots\\a_n\end{pmatrix}
\end{align}
の大きさは以下のように定義する。
\left|\vec{a}\right|=\sqrt{a_1^2+a_2^2+\cdots+a_n^2}
\end{align}
この定義を使うと、ベクトルが何次元であってもうまくいきます。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」







