3次元上の質点のエネルギー｜ぽこラボ勉強ブログ

(※数式が見切れている場合は横スクロールしてください。)

ベクトルの内積を習い終わったので、エネルギーについても3次元で考えてみることにします。やはりここでも質点mに力\(\vec{F}(t)\)が加えられている状況を考えましょう。

一旦、その前に1次元のときの復習です。エネルギーの概念は運動方程式を空間成分で積分することで導入しました。結果として、以下のような方程式を得ましたね。

\begin{align}
\frac{mv^2(t_2)}{2}-\frac{mv^2(t_1)}{2}=\int^{t_2}_{t_1}F(t)v(t)dt
\end{align}

左辺が運動エネルギーの変化を表していて、右辺が仕事を表しています。これを自然に3次元に拡張するとすれば、エネルギーは以下のように与えられると予想できます。

\begin{align}
\frac{m\left|\vec{v}(t)\right|^2}{2}
\end{align}

このとき、エネルギーがベクトル量ではなく、スカラー量であることにも注意が必要です。（運動量のときには3次元に拡張するときにもベクトル量をずっと扱っていました。）

さて、上のように運動エネルギーが与えられるとすると、その瞬間の時間変化は

\begin{align}
\frac{d}{dt}\frac{m\left|\vec{v}(t)\right|^2}{2}
\end{align}

で与えられるはずですし、それを寄せ集めると

\begin{align}
\int^{t_2}_{t_1}\frac{d}{dt}\frac{m\left|\vec{v}(t)\right|^2}{2}dt=\frac{m\left|\vec{v}(t_2)\right|^2}{2}-\frac{m\left|\vec{v}(t_1)\right|^2}{2}
\end{align}

となるはずです。これが1次元のときの左辺に対応しています。この積分を変形していくことで1次元のときの右辺に対応するものが得られることを確認しておきましょう。

まずエネルギーを微分すると以下のような計算になります。

\begin{align}
&\frac{d}{dt}\frac{m\left|\vec{v}(t)\right|^2}{2}\\
=&\frac{m}{2}\frac{d}{dt}\left(v_1^2(t)+v_2^2(t)+v_3^2(t)\right)\\
=&m\left(v_1(t)\dot{v_1}(t)+v_2(t)\dot{v_2}(t)+v_3(t)\dot{v_3}(t)\right)\\
=&m\vec{v}(t)\cdot\dot{\vec{v}}(t)
\end{align}

ここで運動方程式の出番です。運動方程式は以下の形でしたね。

\begin{align}
m\dot{\vec{v}}(t)=\vec{F}(t)
\end{align}

これを使うと、以下のように計算が進められます。

\begin{align}
&\int^{t_2}_{t_1}\frac{d}{dt}\frac{m\left|\vec{v}(t)\right|^2}{2}dt\\
=&\int^{t_2}_{t_1}m\vec{v}(t)\cdot\dot{\vec{v}}(t)dt\\
=&\int^{t_2}_{t_1}\vec{F}(t)\cdot\vec{v}(t)dt
\end{align}

最後の等号のところで運動方程式を代入しました。この結果はたしかに1次元のときの仕事の式に対応していますね。

こうして、3次元のときにもやはり1次元のときと同じ形をした式を導くことができたわけです。1次元のときには強調しませんでしたが、エネルギーと仕事はベクトル量ではなくスカラー量であることを意識することは非常に大事です。

運動方程式はベクトルの方程式。運動量の変化の式はベクトルの方程式。ですが、エネルギーの変化の式はスカラーの方程式。

すなわちエネルギーの式は大きさだけが重要で向きは関係ないということになります。

公式

\begin{align}
\frac{m\left|\vec{v}(t_2)\right|^2}{2}-\frac{m\left|\vec{v}(t_1)\right|^2}{2}=\int^{t_2}_{t_1}\vec{F}(t)\cdot\vec{v}(t)dt
\end{align}

この公式は1次元で議論していたものを素直に拡張した形になっていますが、ここで右辺について少し丁寧に見ておきましょう。

1次元のこれに対応する式ではこの式の右辺は仕事と言い、被積分関数の部分を仕事率と言うという話をしました。

今回もその名前については引き続き使います。

\begin{align}
\int^{t_2}_{t_1}\vec{F}(t)\cdot\vec{v}(t)dt
\end{align}

を仕事と言い、

\begin{align}
\vec{F}(t)\cdot\vec{v}(t)
\end{align}

の部分を仕事率と言います。ここで、\(dt\)の部分まで合わせて見ておくと、仕事というのがより詳しく理解できます。

\begin{align}
\vec{v}(t)dt
\end{align}

は微小時間\(dt\)の間に質点mの進んだ微小距離です。そして、それと\(\vec{F}(t)\)の内積を積み重ねたら仕事になるわけなので、

\begin{align}
\vec{F}(t)\cdot\vec{v}(t)dt
\end{align}

はいわば微小仕事と言い換えることができます。図を見てください。

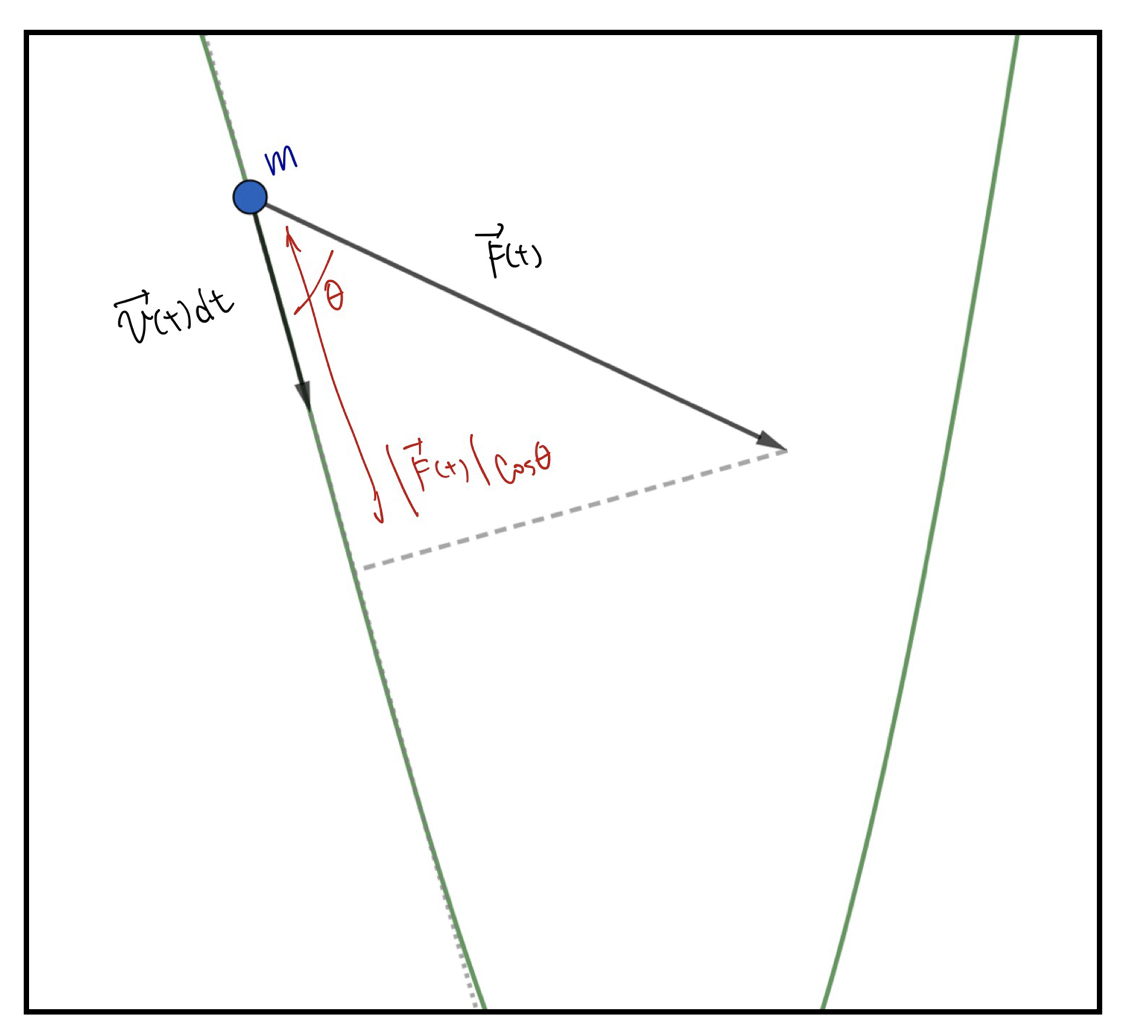
図も参考にすると、この微小仕事は「\(\vec{F}(t)\)の\(\vec{v}(t)\)方向成分」×「\(\vec{v}(t)dt\)の大きさ」なので、さらに言い換えると、「\(\vec{F}(t)\)の微小変位方向の成分」×「微小変位」です。仕事はこれの寄せ集めに過ぎないので、基本は以下のように考えておくといいですね。

「仕事」＝「変位」×「変位方向にかかる力」の寄せ集め

関連リンク

>>ブログ版アラサー高校物理の記事一覧

>>物理の勉強ロードマップ【2019年版】

>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」