(※数式が見切れている場合は横スクロールしてください。)
ベクトルの足し引きについてはこれまでに学習してきました。基本的には中学校で習う文字の扱いと同様にベクトルの足し引きが出来ますし、成分表示されている場合には各成分ごとに計算をすればよかったわけです。
そしてベクトルの足し引きは図形的な性質についても平行四辺形を用いて説明を行いました。
その辺りを踏まえて、この節では、ベクトルの内積を定義しておきます。
ベクトルの内積はベクトルの掛け算の一つです。ベクトルの掛け算には外積というものもあって、そちらはまだしばらく先に学習することになります。
さて、まずは内積の定義を見ておきましょう。
定義
以下のように2つのベクトル\(\vec{a}\)、\(\vec{b}\) があり、その間の角を\(\theta\)とするときベクトルの内積はドットを使って表現し、その意味は次のようになる。
\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{a}=\left|\vec{a}\right|\times\left|\vec{b}\right|\cos\theta
\end{align}
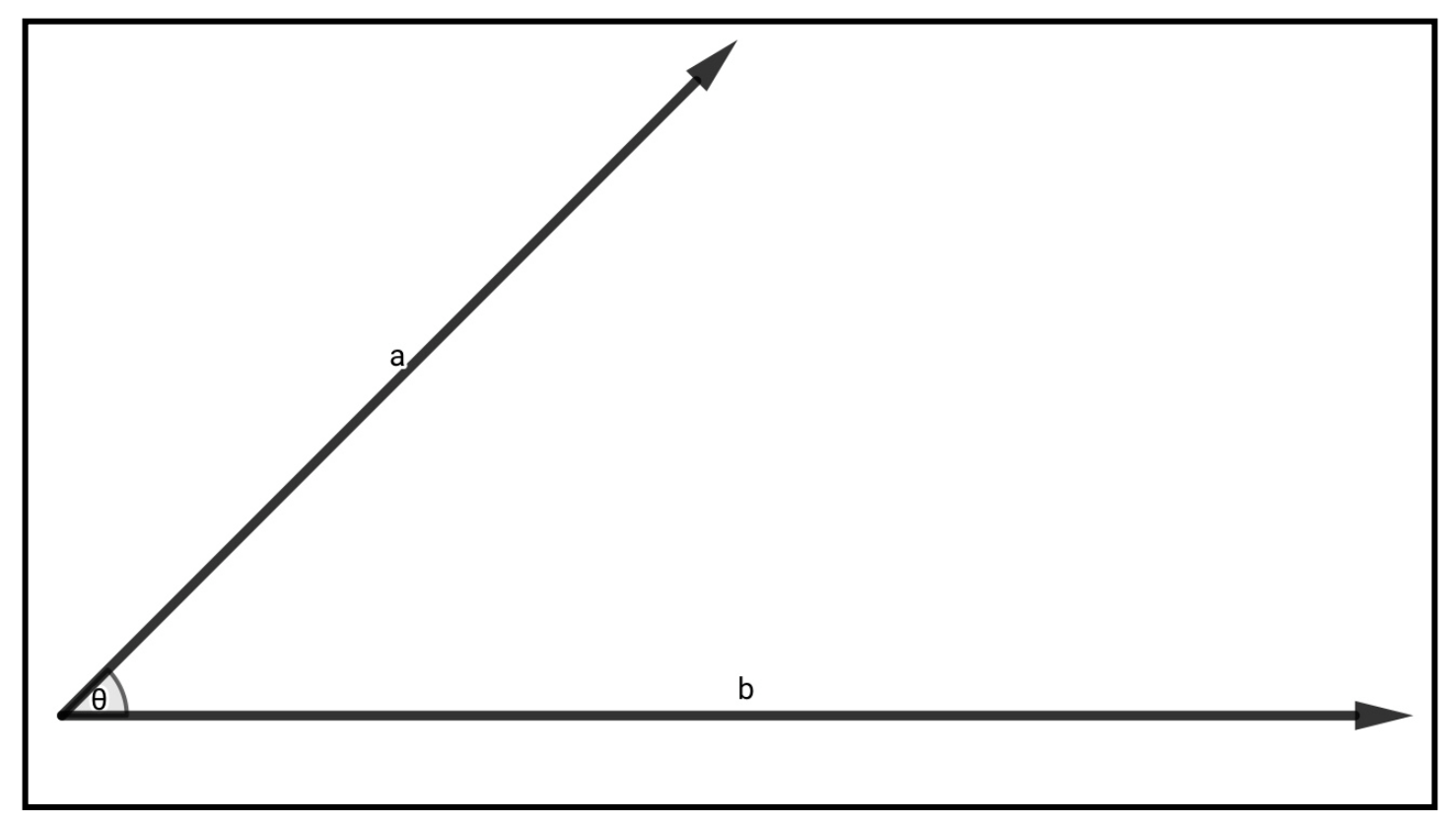
要するに、2つのベクトルの内積はベクトルの大きさ×大きさ×間の角のcosです。定義から内積は順序を交換しても同じものが出てきます。
次の図をもとにベクトルの内積の意味を読み換えることができます。
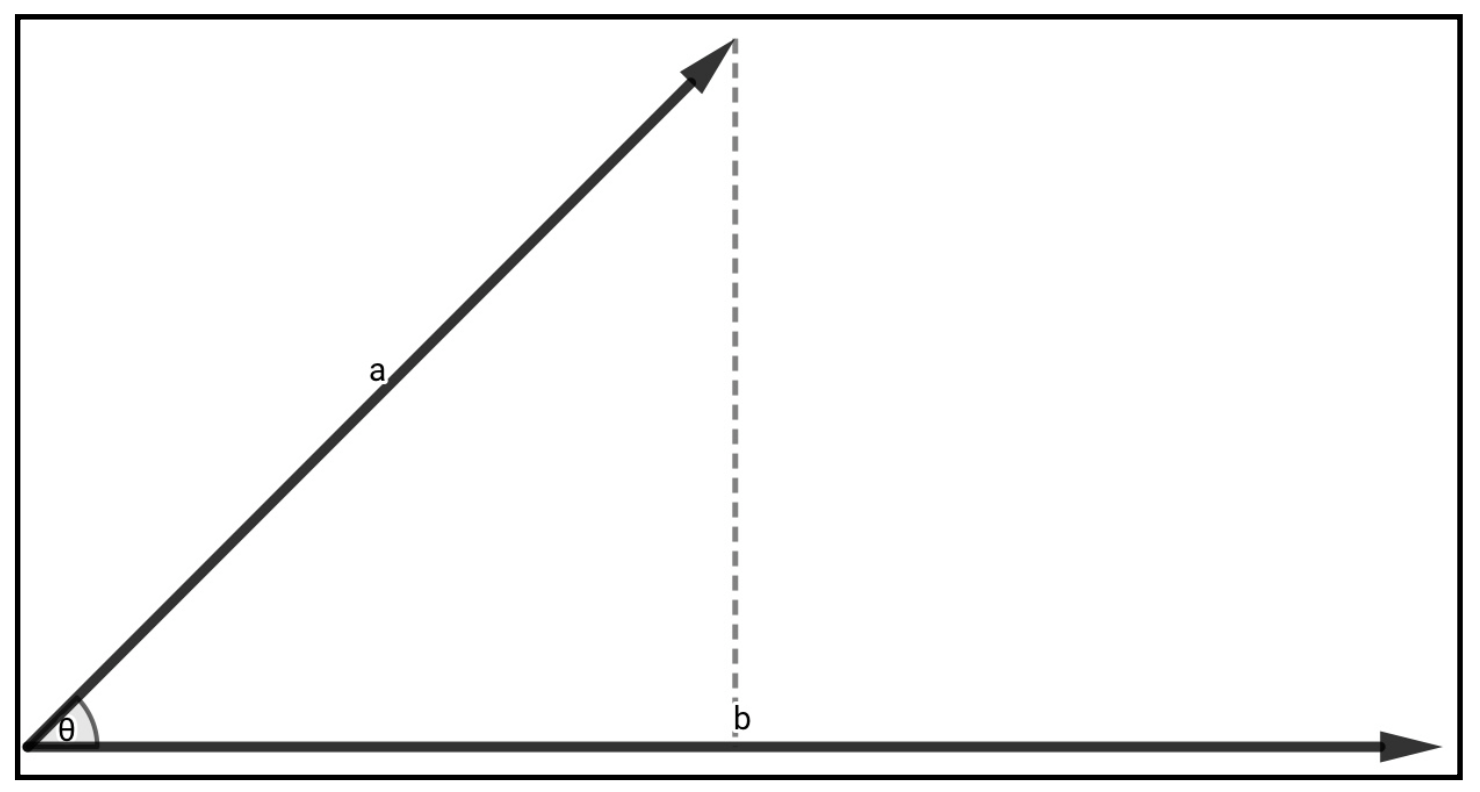
\(\vec{a}\)の長さにcosをかけると、\(\vec{a}\)の\(\vec{b}\)方向成分が出てきます。上の図の通りです。(三角比の定義を思い出してください。)
ですから、\(\vec{a}\)と\(\vec{b}\)の内積は「\(\vec{a}\)の\(\vec{b}\)方向成分」×「\(\vec{b}\)の大きさ」と読み換えることが出来るんです。実はこの考え方が後の力学の章で非常に重要な役割りを果たします。
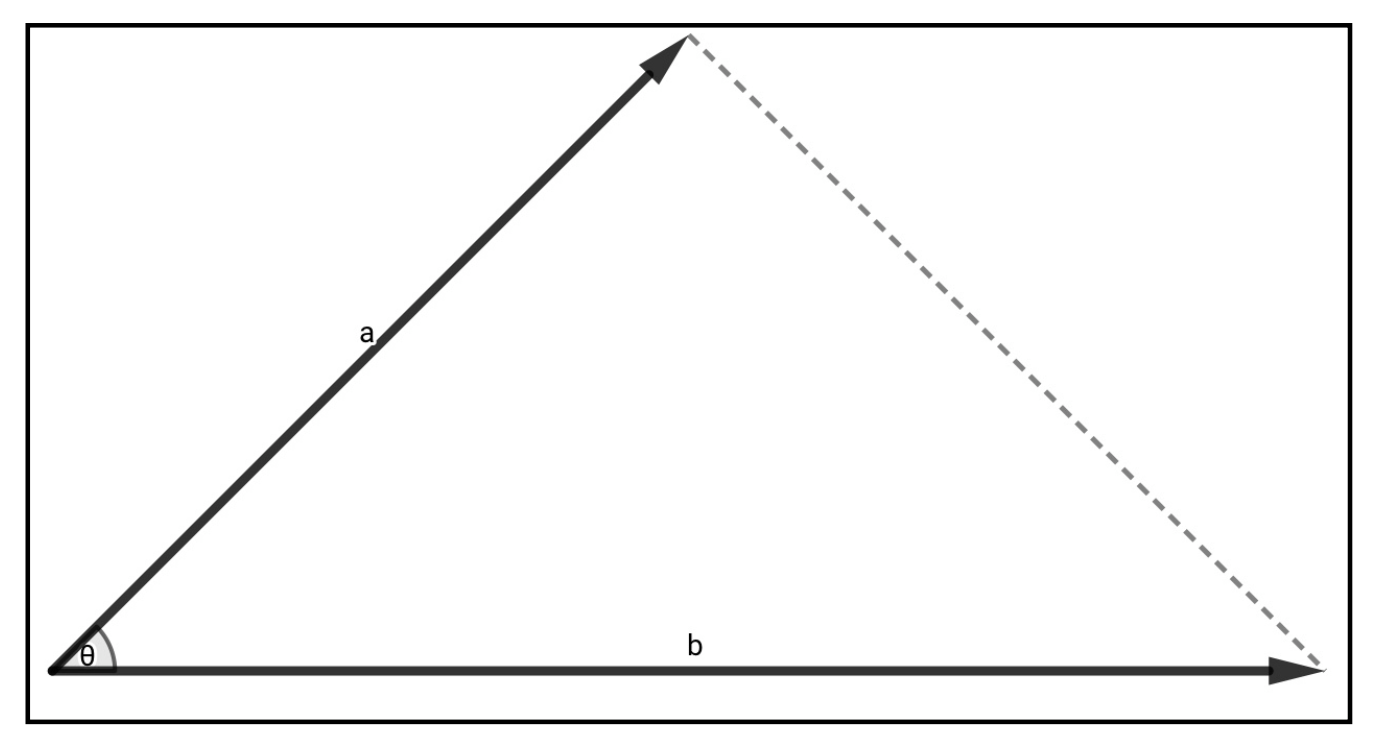
ちなみに\(\vec{a}\)と\(\vec{b}\)の役割を変えて、「\(\vec{b}\)の\(\vec{a}\)方向成分」×「\(\vec{a}\)の大きさ」と考えてもオッケーです。以下の図を参考にしてください。
問題
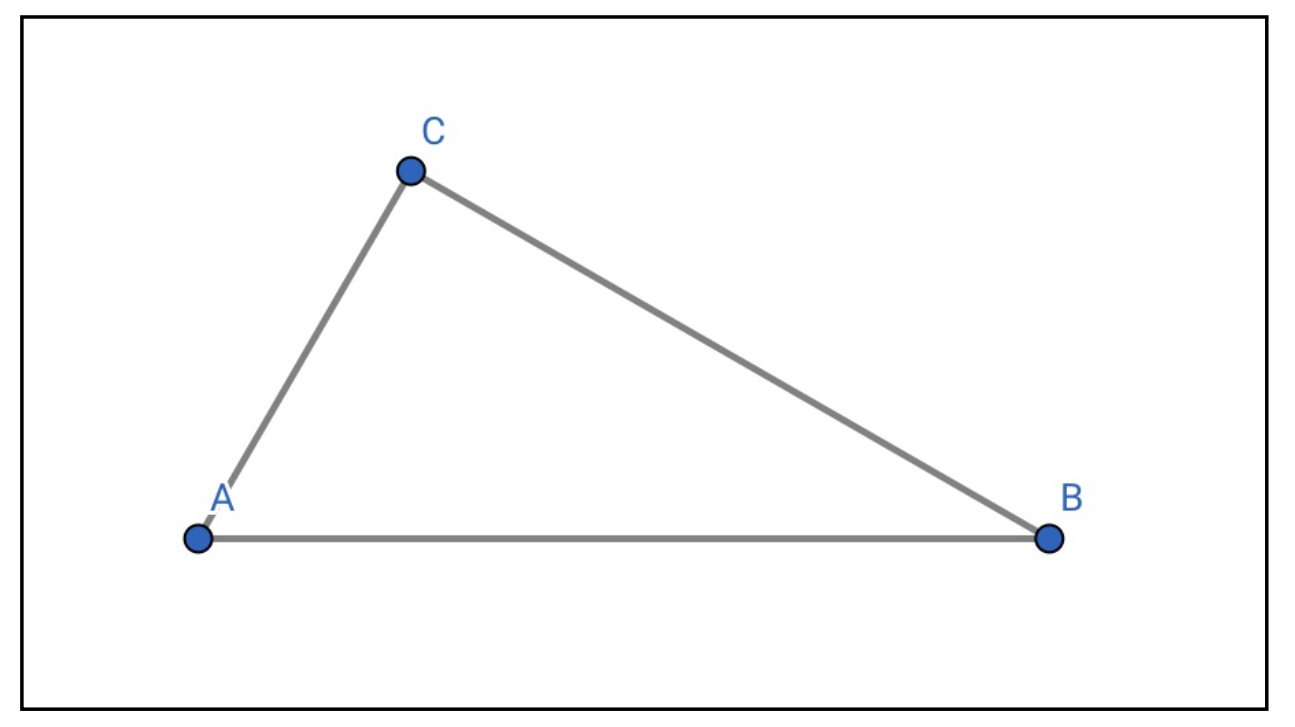
次の三角形ABCについて以下の問いに答えなさい。
ただし、\(AB=2\)、\(BC=\sqrt{3}\)、\(CA=1\)とする。
&1.\quad \vec{AC}\cdot\vec{AB}\\
&2.\quad \vec{BA}\cdot\vec{BC}\\
&3.\quad \vec{CA}\cdot\vec{CB}\\
\end{align}
解答
&1.\quad \vec{AC}\cdot\vec{AB}=\left|\vec{AC}\right|\left|\vec{AB}\right|\cos\angle BAC=2\times1\times \frac{1}{2}=1\\
&2.\quad \vec{BA}\cdot\vec{BC}=\left|\vec{BA}\right|\left|\vec{BC}\right|\cos\angle ABC=2\times\sqrt{3}\times \frac{\sqrt{3}}{2}=3\\
&3.\quad \vec{CA}\cdot\vec{CB}=\left|\vec{CA}\right|\left|\vec{CB}\right|\cos\angle ACB=1\times\sqrt{3}\times 0=0
\end{align}
この問題でも出てきましたが、直角に交わるベクトルの内積は\(0\)になります。これは覚えておいて損はしないでしょう。
ちなみに同じベクトル同士の内積はどうなるでしょうか。
\vec{a}\cdot\vec{a}=\left|\vec{a}\right|\left|\vec{a}\right|\cos0=\left|\vec{a}\right|^2
\end{align}
このようにベクトルの大きさの2乗が出てきます。これも覚えておいてもいい公式ですね。
公式
&\vec{a}\cdot\vec{b}=0\quad(if\quad \vec{a}\perp\vec{b})\\
&\vec{a}\cdot\vec{a}=\left|\vec{a}\right|^2
\end{align}
さて続いては、成分表示されたベクトルでの内積はどのように計算をするのかの話に移りたいと思います。
その前にベクトルの内積の分配法則に触れておきましょう。中学校の数学で展開を習うときに分配法則というものを習ったはずです。それは以下のようなものでした。
(a+b)(c+d)=ac+bc+ad+cd
\end{align}
これと同様にベクトルの内積でも分配法則を使うことが出来ます。
&\left(A\vec{a}+B\vec{b}\right)\cdot\left(C\vec{c}+D\vec{d}\right)\\
=&AC\vec{a}\cdot\vec{c}+BC\vec{b}\cdot\vec{c}+AD\vec{a}\cdot\vec{d}+BD\vec{b}\cdot\vec{d}
\end{align}
このように変形できるわけです。これをベクトルの内積における分配法則と覚えておいてください。分配法則を使って以下の問題に取り組んでみましょう。
問題
計算せよ。
&1.\quad \left(\vec{a}-\vec{b}\right)\cdot\left(\vec{a}+\vec{b}\right)\\
&2.\quad \left|2\vec{a}+\vec{b}\right|^2
\end{align}
解答
内積は順序が逆になっても同じものが出ることさえ意識すればすぐに計算できるでしょう。
&1.\quad \left(\vec{a}-\vec{b}\right)\cdot\left(\vec{a}+\vec{b}\right)=\left|\vec{a}\right|^2-\left|\vec{b}\right|^2\\
&2.\quad \left|2\vec{a}+\vec{b}\right|^2=4\left|\vec{a}\right|^2+4\vec{a}\cdot\vec{b}+\left|\vec{b}\right|^2
\end{align}
さて、もう少し準備すれば成分表示のベクトルでも内積が計算できるようになります。
一般にベクトルは空間の各方向を向く単位ベクトルを使って、成分表示から書き換えることができます。
例えば、
\vec{a}=\begin{pmatrix}a_1\\a_2\end{pmatrix}
\end{align}
というベクトルを\(x\)方向の単位ベクトルと\(y\)方向の単位ベクトルである以下の2つ
\vec{e_1}=\begin{pmatrix}1\\0\end{pmatrix},\quad\vec{e_2}=\begin{pmatrix}0\\1\end{pmatrix}
\end{align}
を使って書き直すことができます。
\vec{a}=&\begin{pmatrix}a_1\\a_2\end{pmatrix}=a_1\begin{pmatrix}1\\0\end{pmatrix}+a_2\begin{pmatrix}0\\1\end{pmatrix}\\
=&a_1\vec{e_1}+a_2\vec{e_2}
\end{align}
この性質を使って内積の公式を見直してみましょう。
\vec{a}\cdot\vec{b}=&\left(a_1\vec{e_1}+a_2\vec{e_2}\right)\cdot\left(b_1\vec{e_1}+b_2\vec{e_2}\right)\\
=&a_1b_1\vec{e_1}\cdot\vec{e_1}+a_2b_2\vec{e_2}\cdot\vec{e_2}+(a_1b_2+a_2b_1)\vec{e_1}\cdot\vec{e_2}
\end{align}
さらに、各方向を向く単位ベクトルはベクトルの公式を使うと、
&\vec{e_1}\cdot\vec{e_2}=0\\
&\left|\vec{e_1}\right|^2=\left|\vec{e_2}\right|^2=1
\end{align}
なので、これも用いると以下のような成分表示の内積の公式を導くことができます。
公式
\vec{a}=\begin{pmatrix}a_1\\a_2\end{pmatrix},\quad\vec{b}=\begin{pmatrix}b_1\\b_2\end{pmatrix}
\end{align}
と与えられているとき、それらの内積は以下のようになる。
\vec{a}\cdot\vec{b}=a_1b_1+a_2b_2
\end{align}
要するに、\(x\)成分同士の掛け算と\(y\)成分同士の掛け算の和ですね。これは2次元以上のときにも同じように使うことできます。
3次元だったら、3つの成分同士の掛け算の和(少しややこしい日本語ですかね?)になりますし、4次元でも5次元でもn次元でも成分表示のベクトルの内積は上のような形になります。
問題
1. 3次元でも同様に上の公式が導出できることを確認せよ。
2.
\vec{a}=\begin{pmatrix}1\\2\\3\end{pmatrix},\quad\vec{b}=\begin{pmatrix}-1\\0\\2\end{pmatrix}
\end{align}
のとき、以下の計算をせよ。
\left|2\vec{a}-\vec{b}\right|^2
\end{align}
解答
1.
まず以下のベクトルを準備します。
&\vec{a}=\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix},\quad\vec{b}=\begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix}\\
&\vec{e_1}=\begin{pmatrix}1\\0\\0\end{pmatrix},\quad\vec{e_2}=\begin{pmatrix}0\\1\\0\end{pmatrix},\quad\vec{e_3}=\begin{pmatrix}0\\0\\1\end{pmatrix}
\end{align}
あとは先ほどの流れをたどるだけです。
\vec{a}\cdot\vec{b}=&(a_1\vec{e_1}+a_2\vec{e_2}+a_3\vec{e_3})\cdot(b_1\vec{e_1}+b_2\vec{e_2}+b_3\vec{e_3})\\
=&a_1b_1+a_2b_2+a_3b_3
\end{align}
これで、3次元でも同様の公式が使えることが示せました。
2.
先に以下の3つを準備しておくと見通しが立ちやすいでしょう。
&\left|\vec{a}\right|^2=1^2+2^2+3^2=14\\
&\left|\vec{b}\right|^2=(-1)^2+0^2+2^2=5\\
&\vec{a}\cdot\vec{b}=1\cdot(-1)+2\cdot0+3\cdot2=5
\end{align}
これを使うと、
\left|2\vec{a}-\vec{b}\right|^2=&4\left|\vec{a}\right|^2-4\vec{a}\cdot\vec{b}+\left|\vec{b}\right|^2\\
=&4\cdot14-4\cdot5+5=41
\end{align}
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」









