(※数式が見切れている場合は横スクロールしてください。)
今回は少し数学的な章ですが、一応物理です。
ただ、大学レベルの物理に進むにつれてこの章くらいの計算は割と頻繁にしなければならなくなりますから、そんなもんなのだと慣れておいて下さい。
ちなみに、計算は頑張って自分の手を使って紙に書いて追いかけるようにしてください。できれば、読み終わった後に何も見ずに計算できるようになっておいてください。
例
球系の物体A(半径\(R\))から質量\(m\)の質点mが受ける万有引力について考える。
物体Aの密度\(\rho(r)\)は物体の中心からの距離\(r\)だけの関数とする。(球対称の質量分布。)
次の図のような位置関係のときの万有引力を考えることにする。
点Oが物体Aの中心、点Pが質点mの位置、OPをつなぐ直線を\(x\)軸とし、点Pの座標は\(x\)とする。
質点mが物質Aから受ける万有引力を\(x\)の関数として表現せよ。
さて、ここから少し長くなるのですが、まず物質Aを薄い球殻の集まりによって出来ていると考えることにします。
順序としては球殻から受ける万有引力を求めて、それを積分して物質Aから受ける万有引力を計算するという形です。
というわけで半径\(r\)で、厚みが\(dr\)の球殻から受ける万有引力を計算していきます。
図のように点Qを\(\theta\)を使って決めます。
角度\(\theta\)から角度\(d\theta\)分の微小角度で表現される球殻上の円状の帯から受ける力を計算していきましょう。
この円状の帯を\(x\)軸の正の方向から見直してみると次の図のようになります。
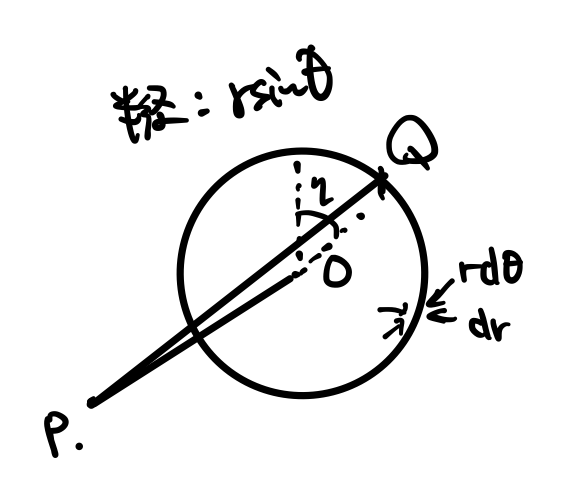
帯を\(0<\eta<2\pi\)の1周で表現することにすると、\(\eta\)から\(\eta+d\eta\)によって表現される微小帯から受ける万有引力の大きさは以下のようになります。
\left((r\sin\theta)d\eta\times rd\theta\times dr\rho(r)\right)\times\frac{mG}{PQ^2}
\end{align}
この最初のかっこでくくられている所が微小な質量になっているわけです。
ちなみに\(PQ\)の大きさは余弦定理で計算することができます。
PQ^2=r^2+x^2-2xr\cos\theta
\end{align}
これを入れると、微小角度\(d\eta\)から来る万有引力の大きさは
\left((r\sin\theta)d\eta\times rd\theta\times dr\rho(r)\right)\times\frac{mG}{r^2+x^2-2xr\cos\theta}
\end{align}
となりますね。ちなみに、角度\(\eta\)の\(0\)から\(2\pi\)までの積分をすると\(x\)方向の成分だけ残ります。他の成分は対称性から消えてしまうわけです。
この万有引力の\(x\)方向の成分は\(\phi\)を使って表現できます。符号にも注意です。
-\left((r\sin\theta)d\eta\times rd\theta\times dr\rho(r)\right)\times\frac{mG}{r^2+x^2-2xr\cos\theta}\cos\phi
\end{align}
これを\(\eta\)で積分すると円状の帯の部分から来る万有引力を計算できます。
&-\int^{2\pi}_{0}\left((r\sin\theta) rd\theta dr\rho(r)\frac{mG}{r^2+x^2-2xr\cos\theta}\cos\phi \right)d\eta\\
=&-2\pi(r\sin\theta) rd\theta dr\rho(r)\frac{mG}{r^2+x^2-2xr\cos\theta}\cos\phi
\end{align}
被積分関数に\(\eta\)はいないので、普通に\(2\pi\)が出てくるだけの積分になります。
今度はこれを\(\theta\)で積分すればうすい球殻から来る万有引力になるわけです。
ただ、\(\phi\)は\(\theta\)に連動して変化するので、\(\phi\)を\(\theta\)で表現してから、計算をしなければなりません。
&PQ\cos\phi+r\cos\theta=x\\
&\cos\phi=\frac{x-r\cos\theta}{\sqrt{r^2+x^2-2xr\cos\theta}}
\end{align}
これを入れて、\(\theta\)で積分した結果を\(f(r)\)とおいて計算していきましょう。
f(r)=-2\pi\int^{\pi}_{0}(r\sin\theta) r dr\rho(r)\frac{mG}{r^2+x^2-2xr\cos\theta}\frac{x-r\cos\theta}{\sqrt{r^2+x^2-2xr\cos\theta}}d\theta
\end{align}
\(\theta\)の積分に集中するために以下のように余計な部分を左辺に移しておきます。
\frac{-f(r)}{2\pi mG\rho(r)dr}=&\int^{\pi}_{0} \frac{r^2\sin\theta(x-r\cos\theta)}{(r^2+x^2-2xr\cos\theta)^{\frac{3}{2}}}d\theta
\end{align}
\(r^2\)は実は右辺に残しておいた方が簡単なので、あえて残しています。
ここからは右辺の積分に集中していきましょう。この積分が一番面倒くさいですので、注意が必要です。
積分するには変数変換が必要です。\(r\cos\theta=t\)と変数変換しましょう。
\theta:0\to\pi\\
t:r\to-r
\end{cases}\end{align}
と、
&\frac{dt}{d\theta}=-r\cos\theta\\
\Longleftrightarrow
&dt=-r\sin\theta d\theta
\end{align}
を使うと先ほどの右辺の積分が以下のように書きなおせます。
\int^r_{-r}\frac{x-t}{(x^2+r^2-2xt)^{\frac{3}{2}}}dt
\end{align}
少し強引に被積分関数の分母を以下のように変形します。
x-t=&\frac{2x^2-2xt}{2x}\\
=&\frac{1}{2x}\left((x^2+r^2-2xt)-(r^2-x^2)\right)
\end{align}
これを入れると積分は次のような形になります。
&\frac{1}{2x}\int^r_{-r}\frac{(x^2+r^2-2xt)-(r^2-x^2)}{(x^2+r^2-2xt)^{\frac{3}{2}}}dt\\
=&\frac{1}{2x}\int^r_{-r}\frac{x^2+r^2-2xt}{(x^2+r^2-2xt)^{\frac{3}{2}}}dt
-\frac{1}{2x}\int^r_{-r}\frac{r^2-x^2}{(x^2+r^2-2xt)^{\frac{3}{2}}}dt
\end{align}
第１項の不定積分は次のように書けます。
&\int \frac{dt}{\sqrt{x^2+r^2-2xt}}\\
=&-\frac{\sqrt{x^2+r^2-2xt}}{x}+C
\end{align}
第2項の不定積分は次のように書けます。
&\int\frac{r^2-x^2}{(x^2+r^2-2xt)^{\frac{3}{2}}}dt\\
=&\frac{r^2-x^2}{x\sqrt{x^2+r^2-2xt}}+C
\end{align}
これまでに見た積分の中でも割と難しい方だと思うので、難しかったら、積分結果の方を微分してちゃんと被積分関数に戻ることは確認しておくといいでしょう。
さて、この不定積分の結果を先ほどまでの大元の積分に戻すと
&\frac{1}{2x}\int^r_{-r}\frac{x^2+r^2-2xt}{(x^2+r^2-2xt)^{\frac{3}{2}}}dt
-\frac{1}{2x}\int^r_{-r}\frac{r^2-x^2}{(x^2+r^2-2xt)^{\frac{3}{2}}}dt\\
=&\frac{1}{2x}\left[-\frac{\sqrt{x^2+r^2-2xt}}{x}-\frac{r^2-x^2}{x\sqrt{x^2+r^x-2xt}}\right]^r_{-r}\\
=&\frac{1}{2x}\left[-\frac{\left|x-r\right|}{x}+\frac{\left|x+r\right|}{x}-\frac{r^2-x^2}{x}\left(\frac{1}{\left|x-r\right|}-\frac{1}{\left|x+r\right|}\right)\right]
\end{align}
はい、ここまでが長々とした積分の結果です。
ところで、\(\sqrt{a^2}=\left|a\right|\)となることを覚えていないと解けないので、注意してください。もちろんこれは絶対値の記号です。
絶対値に関しては絶対値の中身が正なのか負なのかというので場合分けが必要です。
\(x>r\)のときと、\(x<r\)のときで場合分けしなければなりません。
\frac{-f(r)}{2\pi mG\rho(r)dr}=
\begin{cases}
\frac{2r}{x^2}\quad(x>r)\\
0\quad(x<r)
\end{cases}
\end{align}
まず\(x<r\)のときには万有引力はゼロになります。
\(x>r\)のときには整理すると次のようになります。
f(x)=-\frac{mG}{x^2}\times 4\pi r^2\rho(r)dr
\end{align}
\(\times\)記号の後の\(4\pi r^2 \rho(r)dr\)に関しては、薄い球殻の質量に相当します。
最初に戻って、球殻を集めてくるとどうなるかというのもここまでの計算でほとんど理解したことになります。
物体Aから受ける万有引力は球殻分の寄与を集めてくればいいので、
F(x)=&-\frac{mG}{x^2}\int^R_{0}4\pi r^2\rho(r)dr\\
=-\frac{mG}{x^2}&\int^x_{0}4\pi r^2\rho(r)dr
\end{align}
となります。2つ目の等号は先ほどの計算の結果として、自分よりも内側にある分だけの質量が物体Aの中心に集まっているとして、計算したものとなります。
自分よりも外側の部分から来る万有引力はキャンセルされるというのがポイントです。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」
東大理系攻略法を
解説したPDF販売中！
中高一貫校に行かなくても、塾に行かなくても、独学で受かるための勉強法を完全解説！
全科目の参考書
全参考書の使い方
受験までの勉強スケジュール
が全てわかります！
今だけ！100様限定60%OFF！
さらに24時間以内なら返金保証つき！
無料サンプル公開！
