(※数式が見切れている場合は横スクロールしてください。)
ここでだ円と双曲線の学習をすることにします。しばらく物理の話が続いたので、少しだけ数学の章を進めて次に進むことにしましょう。
まずだ円です。
だ円は2つの焦点を決めてそれぞれの焦点からの距離の和が等しい全ての点をプロットした結果、描かれる曲線(軌跡)です。
具体的に以下の例で話を進めていきますね。
例
2点F\((c,0)\)、点F’ \((-c,0)\)が\(xy\)平面に固定されている。(\(c>0\))
点P\((x,y)\)が以下の性質
FP+F’P=2a\quad (a>c)
\end{align}
を満たすとき、点Pの座標の\(x,y\)はどのような関係になるか。
(\(x\)、\(y\)の満たす方程式を求めよ。)
まず図から確認しましょう。
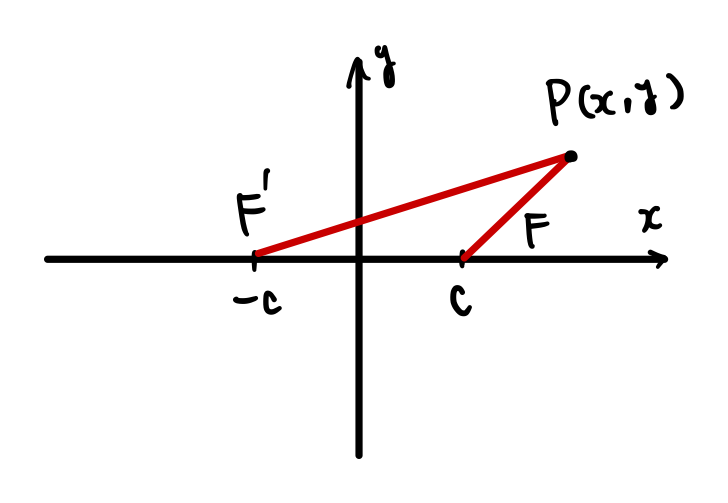
例で与えられた条件を図示するとこんな感じになっています。
三平方の定理を以下のような図に用いると、FPとF’Pの大きさを計算できます。
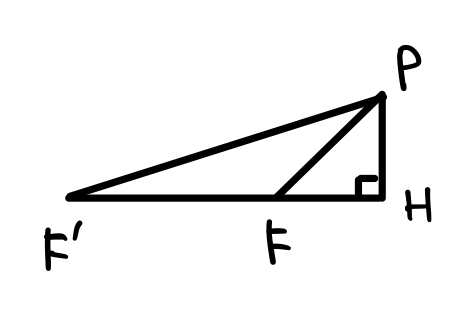
FP=\sqrt{(x-c)^2+y^2}\\
F’P=\sqrt{(x+c)^2+y^2}
\end{cases}\end{align}
これと\(FP+F’P=2a\)を絡めると以下のようになります。ちょっと長い計算なんですけど、頑張って計算してみましょう。
&\sqrt{(x-c)^2+y^2}+\sqrt{(x+c)^2+y^2}=2a\\
\Longleftrightarrow
&\sqrt{(x-c)^2+y^2}=2a-\sqrt{(x+c)^2+y^2}\\
\Longleftrightarrow
&(x-c)^2+y^2=4a^2-4a\sqrt{(x+c)^2+y^2}+(x+c)^2+y^2\\
\Longleftrightarrow
&-2cx=4a^2-4a\sqrt{(x+c)^2+y^2}+2cx\\
\Longleftrightarrow
&4a\sqrt{(x+c)^2+y^2}=4a^2+4cx\\
\Longleftrightarrow
&a\sqrt{(x+c)^2+y^2}=a^2+cx\\
\Longleftrightarrow
&a^2(x+c)^2+a^2y^2=a^4+2a^2cx+c^2x^2\\
\Longleftrightarrow
&(a^2-c^2)x^2+a^2y^2=a^2(a^2-c^2)\\
\Longleftrightarrow
&\frac{x^2}{a^2}+\frac{y^2}{a^2-c^2}=1
\end{align}
ここで、\(a^2-c^2>0\)なので、\(b=\sqrt{a^2-c^2}\)とおくことができます。
そうすると最終的な形は以下のものです。
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1
\end{align}
これが点Pの\((x,y)\)が満たす方程式で、だ円の方程式と言います。
まとめます。
公式
だ円の方程式が以下のように書けて、
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1
\end{align}
\(a>b\)を満たすとき、このだ円の焦点は\((\pm \sqrt{a^2-b^2},0)\)となる。
\(a<b\)を満たすときには、だ円の焦点は\((0,\pm\sqrt{b^2-a^2})\)となる。
具体的に、だ円の例を見ておきましょう。
たとえば、
\frac{x^2}{3^2}+\frac{y^2}{2^2}=1
\end{align}
は\(3>2\)なので、焦点は\((\pm\sqrt{5},0)\)です。実際に描いてみると
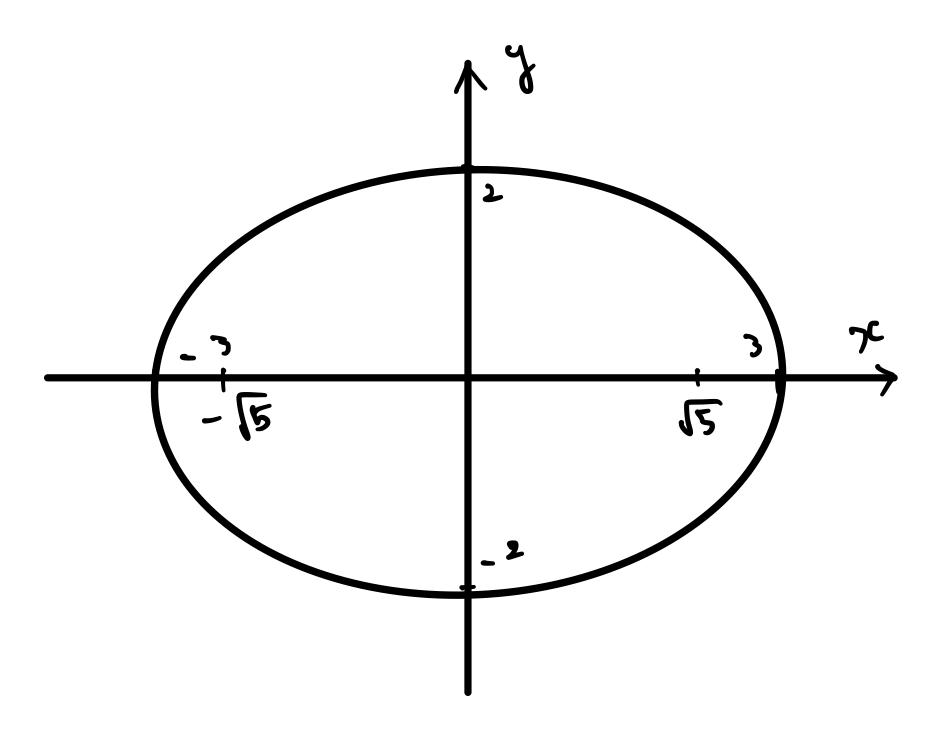
というような形になります。
描き方のイメージとしては、\(x=0\)つまり\(y\)軸上だと、\(y=\pm2\)のときに方程式を満たします。
同様に\(y=0\)のときには\(x=\pm 3\)で方程式を満たします。
あと焦点を計算するのはこの節で導出したように頑張るのはしんどいので覚えておく方がいいと思います。
ここで短半径と長半径という言葉を覚えておいた方がいいです。
この例でいうと、短半径が\(2\)で長半径が\(3\)です。
そんなに難しくないですよね。
円を少し変形したものがだ円とみることができますから、円と違って中心からの距離(=半径)は場所によって違います。
一番長い所を長半径、一番短い所を短半径と言います。
このあたりを踏まえて、問題を1問解いておきましょう。
問題
焦点\((0,\pm4)\)、短半径の長さ\(3\)のだ円の方程式を求めよ。
解答
求めるだ円をまず
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1
\end{align}
とおきます。焦点の配置に着目すると縦長ですから、\(a=3\)であることは確定します。
あとは焦点を計算する式に着目して、
&\pm\sqrt{b^2-a^2}=\pm4\\
\Longleftrightarrow
&b=5
\end{align}
です。最終的に
\frac{x^2}{3^2}+\frac{y^2}{5^2}=1
\end{align}
となります。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」








