(※数式が見切れている場合は横スクロールしてください。)
今回はすぐに物理に戻ってきました。
単振動はあくまでも1次元的な運動でした。これまでの学習でもそうでしたが、1次元の次には2次元3次元と次元を上げて勉強していくのが通例です。
質点が2次元上を運動していて、原点からの位置が以下のように時刻の関数で与えられている状態を考えてみましょう。
\vec{x}(t)=\begin{pmatrix}x(t)\\y(t)\end{pmatrix}=\begin{pmatrix}r\cos\omega t\\r\sin \omega t\end{pmatrix}
\end{align}
式を見ると\(x\)方向にも\(y\)方向にも半径\(r\)で単振動をしているような状態ですね。
実はこの質点は等速円運動をしていると表現することができます。それを理解するためには、質点の描く軌跡が円であることと、質点の速度が時間によらず一定であることを確認すればいいですね。
まず、軌跡を確認するためには、時刻\(t\)を消去すれば大丈夫です。
x=r\cos\omega t\\
y=r\sin\omega t
\end{cases}\end{align}
の両辺を2乗して辺々を足し算すればが消えてくれます。
x^2+y^2=r^2
\end{align}
が軌跡ですね。これは正しく円の方程式です。次に質点の速さを計算してみましょう。
\vec{v}(t)=\dot{\vec{x}}(t)=\begin{pmatrix}-r\omega\sin\omega t\\r\omega\cos \omega t\end{pmatrix}
\end{align}
これの大きさを計算してみると、
&\left|\vec{v}(t)\right|^2=r^2\omega^2\sin^2\omega t+r^2\omega^2\cos^2\omega t=r^2\omega^2\\
\Longleftrightarrow
&\left|\vec{v}(t)\right|=r\omega
\end{align}
となり、等速であることもわかりました。等速で円軌道を動くのですから、等速円運動です。
次に、等速円運動するためにどのような力が必要なのか考えなければなりません。そのためには加速度を計算して必要な力を計算すればいいですね。
加速度は速度をもう一度微分すれば出てきます。
\vec{a}(t)=\dot{\vec{v}}(t)=\begin{pmatrix}-r\omega^2 \cos\omega t\\-r\omega^2\sin \omega t\end{pmatrix}=-\omega^2\vec{x}(t)
\end{align}
当たり前ですけど、各成分が単振動の形をしているのですから、ベクトルで表示しても単振動の形と同じものが出てくるはずですよね。
運動方程式から等速円運動に必要な力は以下のようになります。
\vec{F}(t)=m\vec{a}(t)=-m\omega^2\vec{x}(t)
\end{align}
図を見るともうすこしわかりやすいかもしれません。
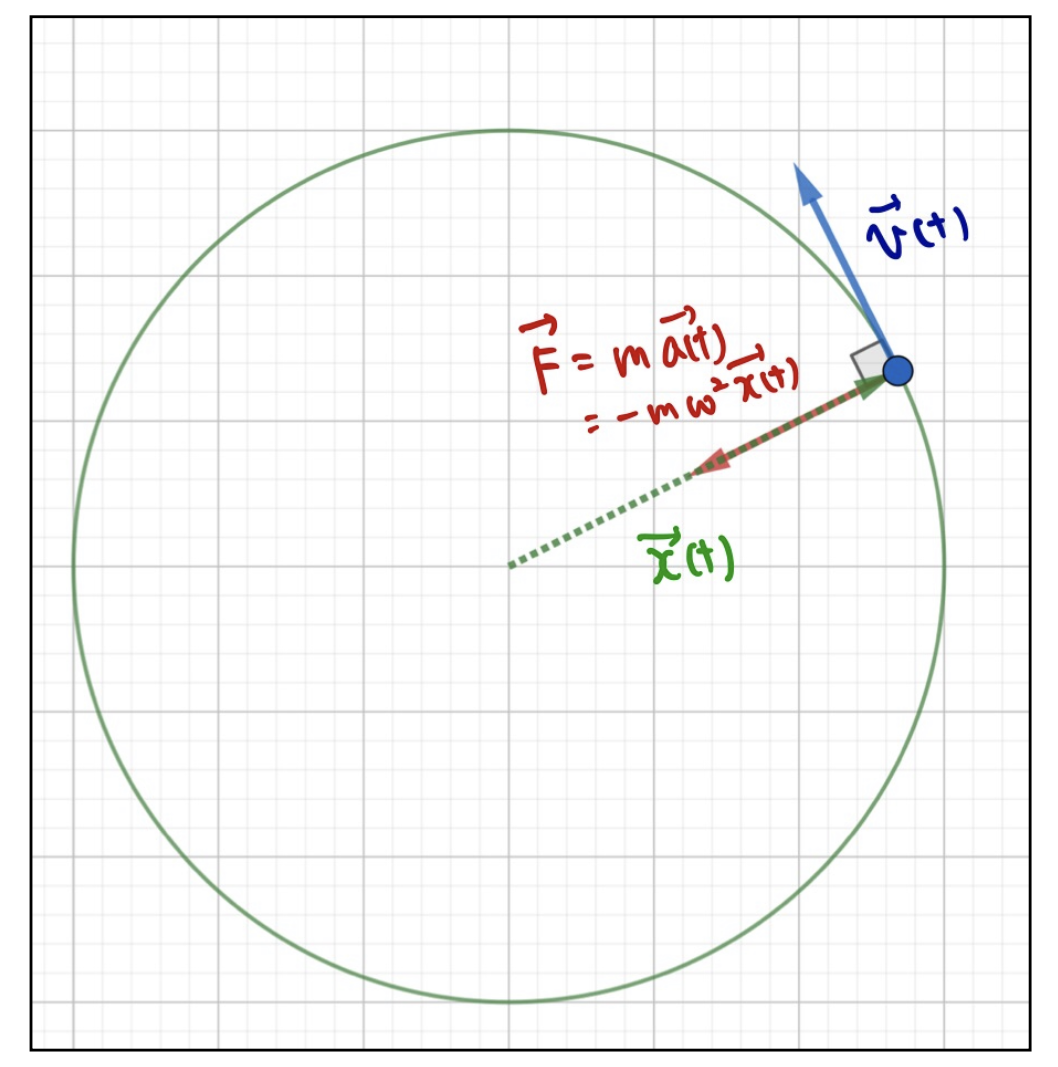
運動の方向に対して常に垂直で中心に向かって力をかけることで円運動をさせられます。この力のことを向心力と言います。
速度を各瞬間ごとに中心に向くように変えていかなければ円運動はできないので、向心力が円運動の中心に向くのは自然ですね。
この円運動の周期ですが、円周\(2\pi r\)を速度\(r\omega\)で運動しているので、
T=\frac{2\pi r}{r\omega}=\frac{2\pi}{\omega}
\end{align}
と計算できます。\(2\pi\)の角度（1周）を1秒あたり\(\omega\)の角度だけ進むと考えると、\(\omega\)のことを角速度と呼んでいたのも納得できるのではないかと思います。
さて、ここまでを（少しだけ一般化して）まとめておきましょう。
公式
質点mの位置が以下のように時刻の関数で表されるとき、
\vec{x}(t)=\begin{pmatrix}x(t)\\y(t)\end{pmatrix}=\begin{pmatrix}r\cos(\omega t+\theta)\\r\sin(\omega t+\theta)\end{pmatrix}
\end{align}
質点は以下の軌跡を円運動する。
x^2+y^2=r^2
\end{align}
質点の速さと周期は
v=r\omega\\
T=\frac{2\pi}{\omega}
\end{cases}\end{align}
という風に角速度と半径で表される。この回転のためには向心力が必要で、その大きさは
\left|\vec{F}(t)\right|=\left|-m\omega^2\vec{x}(t)\right|=mr\omega^2
\end{align}
となる。向きは円運動の中心方向を指す。
各座標の三角関数の引数は\(\omega t+\theta\)としました。これで、どこから円運動がスタートしても対応できる形になっています。計算を追えば分かりますが、この\(\theta\)は周期や向心力の大きさなどには悪さをしません。ちなみにこの引数全体のことを位相と呼ぶことがありますので、その名前も覚えておいてください。
ここで問題を1つ扱って円運動に少し慣れておきましょう。
問題
以下の図のように地面に逆向きに固定された円すいがある。この円すいの中は空洞になっていて、地面から高さ\(h\)の位置で質点mは等速円運動を行なっている。
円すいの形は図のように\(R\)と\(H\)で与えられているものとする。このとき、円運動の速さ\(v\)と高さ\(h\)の関係を求めよ。
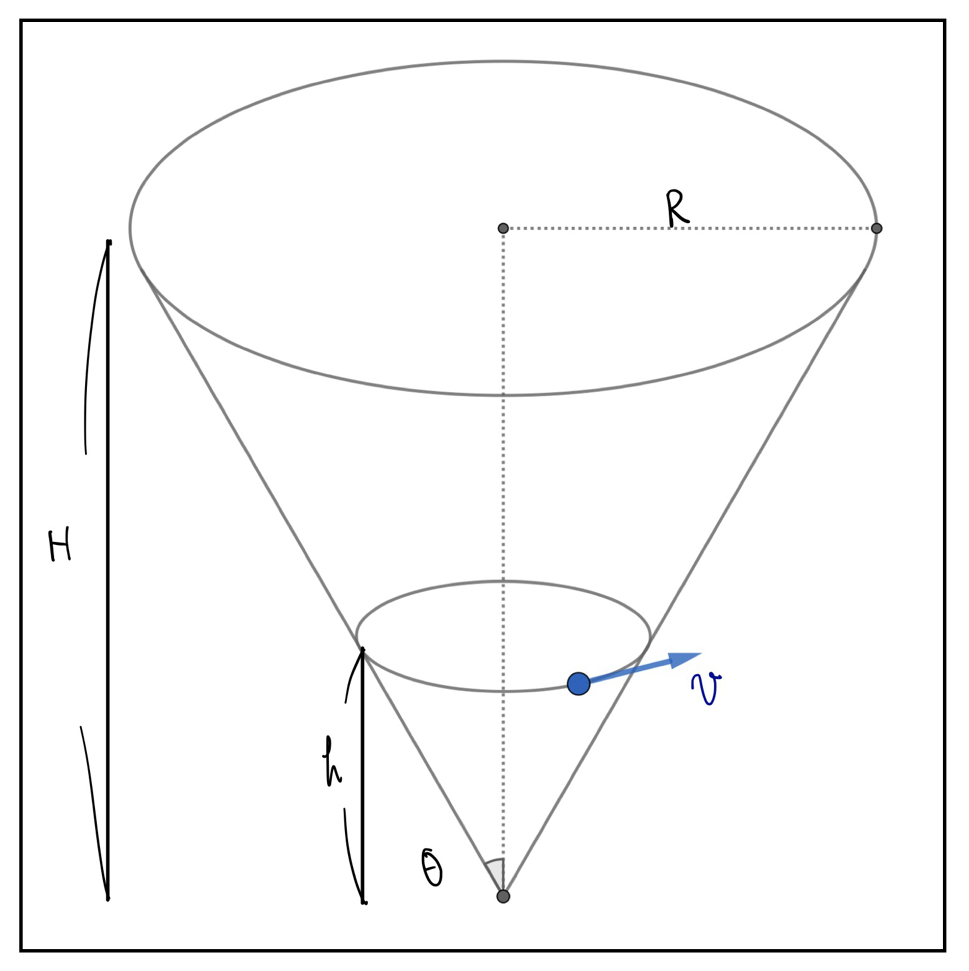
解答
まずはこの円運動の半径から求めてみましょう。半径を求めるのは単なる図形の問題です。
\(\tan\theta=R/H\)となりますので、これから円運動の半径は
r=h\tan\theta=\frac{hR}{H}
\end{align}
とわかります。次に円運動の面に関する運動方程式ですが、向心力は以下の図のように垂直抗力の面内成分ですね。
上下方向（面に垂直）にはつりあっているはずなので、以下の2式が成り立ちます。
N\cos\theta=mr\omega^2\\
N\sin\theta=mg
\end{cases}\end{align}
1つ目の式は運動方程式で、2つ目の式はつりあいの式です。
ここで、円運動をしているときには
v=r\omega
\end{align}
が成り立ちますので、これを使って運動方程式から角速度を消去すると
N\cos\theta=m\frac{v^2}{r}
\end{align}
となります。この\(N\)を消すためにつりあいの式を用いると以下のように書き直せます。
&\frac{mg}{\tan\theta}=m\frac{v^2}{r}\\
\Longleftrightarrow
&v=\sqrt{\frac{gr}{\tan\theta}}=\sqrt{gh}
\end{align}
こうして、\(v\)と\(h\)の関係がわかりました。逆さの円すいの高い位置で円運動をさせようと思うとそれだけ速い速度で運動する必要があるということですね。
これは直感に従った結果になっていませんか？
等速ではない円運動も最後に1つだけ勉強しておきましょう。以下のようなセッティングで勉強することにしましょう。
例
半径の円柱を図のように横にして置いて固定する。ある瞬間に質点mを1番低い所に置いて、図のように初速度\(v_0\)を与えると、この円柱を垂直に切った面内を円運動し始めた。
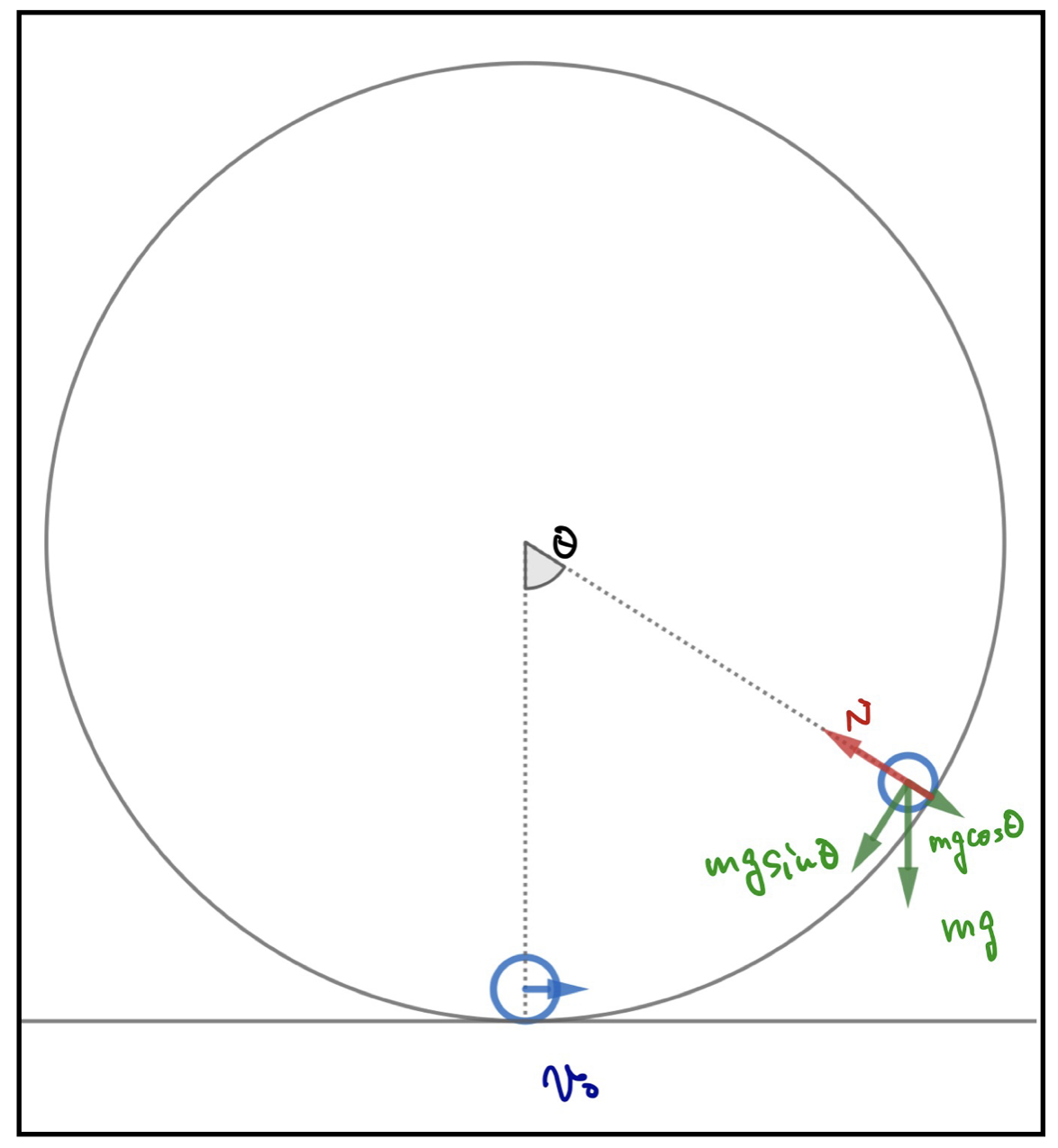
1周して元の位置に戻って来させるためには初速度はいくら以上でないといけないのか計算せよ。
図に書き込みましたが、垂直抗力と重力しかないので、質点が円軌道を上に登って行くたびに重力によって負の仕事がなされて速度は遅くなっていきます。ですから、先程までとは違って等速ではない円運動になっていますね。
等速ではない円運動の場合には、角速度は一定ではないので、それは使わず\(v\)を使った方が考えやすくなります。速度であれば、力学的エネルギーの保存則から出せる場合が多いからですね。
そこで、まずは力学的エネルギーの保存則から図のような角度\(\theta\)のところに質点があるときの速度\(v(\theta)\)を求めてみましょう。
&\frac{1}{2}mv_0^2=mgr(1-\cos\theta)+\frac{1}{2}m\left(v(\theta)\right)^2\\
\Longleftrightarrow
&v(\theta)=\sqrt{v_0^2-2gr(1-\cos\theta)}
\end{align}
このようになります。次にこの瞬間の運動方程式を考えます。向心力は実は速度に依存すると考えてもいいです。というのは以下のように公式の書き換えができるからですね。
\left|\vec{F}\right|=mr\omega^2=m\frac{v^2}{r}
\end{align}
これを元に回転の運動方程式を考えると、
m\frac{\left(v(\theta)\right)^2}{r}=N-mg\cos\theta
\end{align}
となります。向心力は垂直抗力と重力の中心向き成分の合力で計算できます。
ここまでで登場していない考え方なのですが、垂直抗力がゼロになるとその瞬間に抗力を得ている面との接触がなくなります。この考え方を用います。運動方程式を少し変形して、垂直抗力について解くと同時に\(v(\theta)\)の値も代入すると、以下のように計算できます。
N=&m\frac{\left(v(\theta)\right)^2}{r}+mg\cos\theta\\
=&m\frac{v_0^2-2gr(1-\cos\theta)}{r}+mg\cos\theta\\
=&m\left(\frac{v_0^2}{r}-2g+3g\cos\theta\right)
\end{align}
いま、\(\theta\)は1周つまり\(0\leq\theta\leq2\pi\)の範囲で考えますから、この範囲の中でが最も小さくなるのは\(\theta=\pi\)のときですね。その瞬間に垂直抗力がゼロより大きければいいので、以下のような不等式を作ることができます。
N=&m\left(\frac{v_0^2}{r}-2g+3g\cos\theta\right)
\geq m\left(\frac{v_0^2}{r}-5g\right)>0\\
\Longleftrightarrow
&v_0>\sqrt{5gr}
\end{align}
こうして、初速度がいくらあれば、質点が円柱から離れることなく1回転できるかわかりました。
ちなみにが小さくなる周辺では、重力が向心力を担ってくれる割合が増えているため、垂直抗力が必要なくなるのですね。
本当は、質点の上に乗っている人から相対的に運動を見る時にはもう少し理解しやすい形で説明できるのですが、それはまた後の章で勉強することにしましょう。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」
東大理系攻略法を
解説したPDF販売中！
中高一貫校に行かなくても、塾に行かなくても、独学で受かるための勉強法を完全解説！
全科目の参考書
全参考書の使い方
受験までの勉強スケジュール
が全てわかります！
今だけ！100様限定60%OFF！
さらに24時間以内なら返金保証つき！
無料サンプル公開！
