(※数式が見切れている場合は横スクロールしてください。)
先ほど、逆関数を定義するところで実は合成関数の概念は導入しています。言葉で説明すると、合成関数は以下のようになります。
ある関数に入力1を入れて、出力1を得ます。その出力1を今度は入力2として別の関数に入れて、出力2を得ます。このとき、入力1から出力2を得る関数を合成関数と言います。
数式で表すと例えば、関数\(g\)の入力に\(f(x)\)を使うようなものですね。図を見ていただいた方がわかりやすいかもしれません。
図は以下のようになっています。
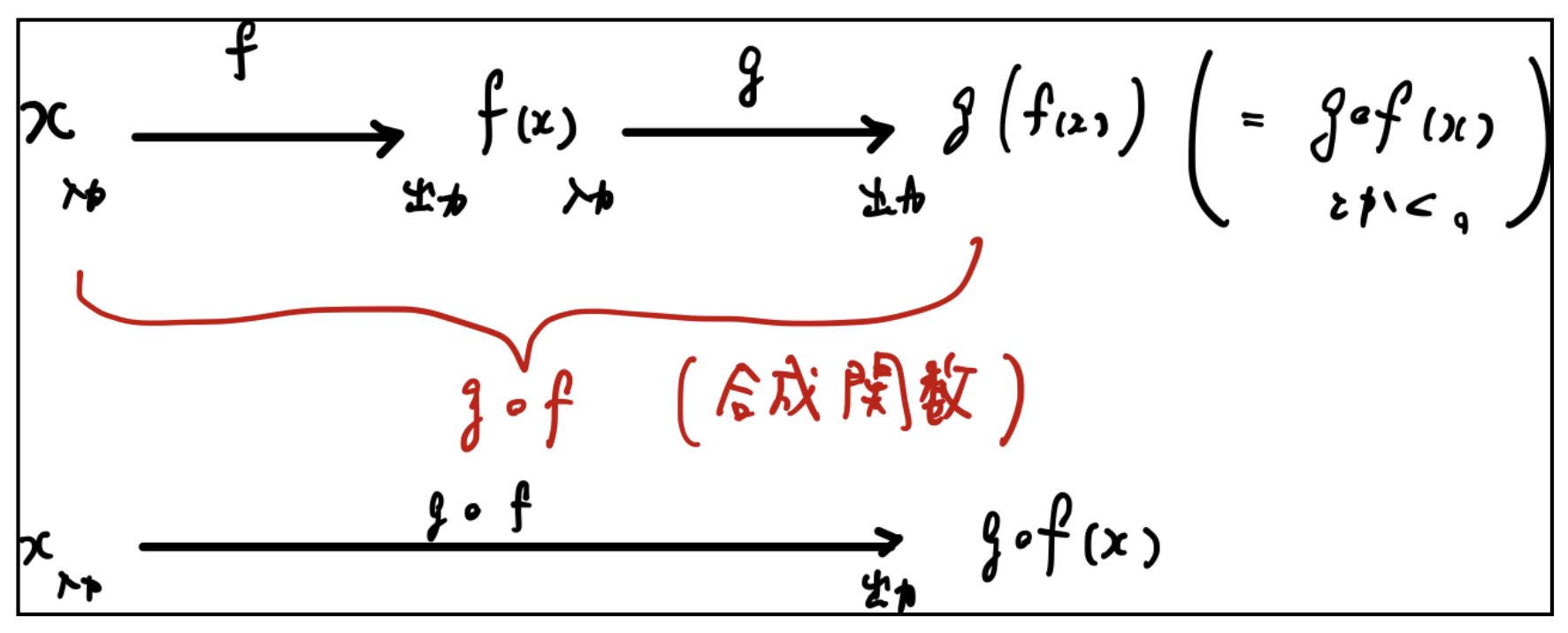
問題を解いてみると、もう少しスッキリ理解することができるでしょう。
問題
以下のように関数\(f\)と関数\(g\)が与えられているときに、合成関数\(f\cdot g\)と\(g\cdot f\)を求めよ。
1.
\begin{align}
f(x)=x^2,\quad g(x)=\sin x
\end{align}
f(x)=x^2,\quad g(x)=\sin x
\end{align}
2.
\begin{align}
f(x)=3x+1,\quad g(x)=\cos x
\end{align}
f(x)=3x+1,\quad g(x)=\cos x
\end{align}
解答
1.
問題を解くだけなら答えだけで大丈夫ですかね。
\begin{align}
&f\cdot g(x)=f(g(x))=\left(g(x)\right)^2=\sin^2 x\\
&g\cdot f(x)=g(f(x))=\sin(f(x))=\sin x^2
\end{align}
&f\cdot g(x)=f(g(x))=\left(g(x)\right)^2=\sin^2 x\\
&g\cdot f(x)=g(f(x))=\sin(f(x))=\sin x^2
\end{align}
三角関数の章で学習したように、指数のついている位置に注意してくださいね。
2.
\begin{align}
&f\cdot g(x)=f(g(x))=3g(x)+1=3\cos x+1\\
&g\cdot f(x)=g(f(x))=\cos(f(x))=\cos(3x+1)
\end{align}
&f\cdot g(x)=f(g(x))=3g(x)+1=3\cos x+1\\
&g\cdot f(x)=g(f(x))=\cos(f(x))=\cos(3x+1)
\end{align}
このように先にどちらの関数に入力するかによって一般に合成関数は異なることがわかります。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」
スポンサーリンク
東大卒の現役塾講師が
東大理系攻略法を
解説したPDF販売中！
東大理系攻略法を
解説したPDF販売中！
中高一貫校に行かなくても、塾に行かなくても、独学で受かるための勉強法を完全解説！
全科目の参考書
全参考書の使い方
受験までの勉強スケジュール
が全てわかります！
今だけ！100様限定60%OFF！
さらに24時間以内なら返金保証つき！
会員数500万人超の「note」で
無料サンプル公開！
無料サンプル公開！
