(※数式が見切れている場合は横スクロールしてください。)
前回の数学の章は少し長かったので、少し息切れしてないですか?大丈夫ですかね。
今回から単振動という節に入ります。どんなのがあるかというと、例えばお祭りなんかで見かける水風船とかビヨンビヨンてなりますよね。あれは単振動です。他にも、振り子をちょっとだけ揺らしてみるとそれは単振動になってます。あんまり大きく揺らすと高校生の物理の範囲では理解できないんですけどね。
何はともあれ、そういった単振動についてここで学ぶこととしましょう。
まずは以下のような例を考えます。壁にばねをくっつけて、逆サイドに質点をくっつけるパターンです。床と質点の間に摩擦はないとしましょう。重力も無視です。
これを自然長から伸ばしたり縮ませたりしてから、手を離すと単振動を始めます。今回は最初に\(d\)だけ縮めた状態を初期状態としましょう。(図参照。)ある時刻\(t\)のときの質点の位置を\(x(t)\)とすると、質点はばねから\(-kx(t)\)の力を受けます。
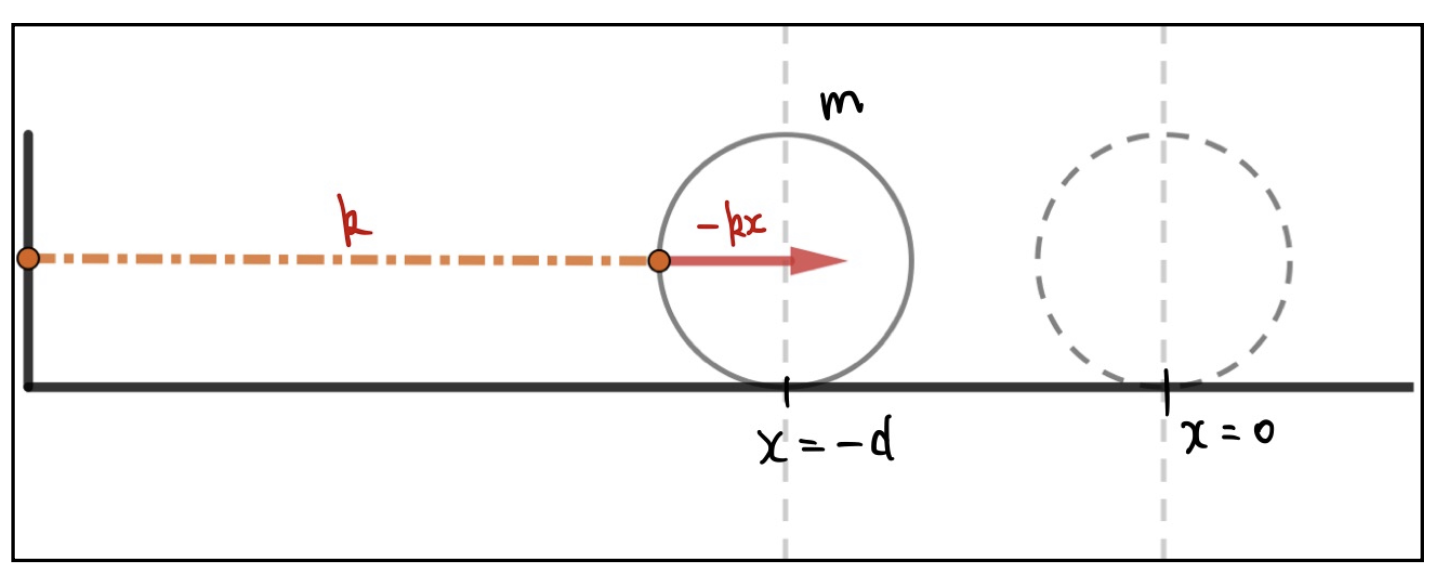
これを運動方程式にすると以下のような式が得られます。
m\ddot{x}(t)=-kx(t)
\end{align}
少し変形すると前の節で勉強した2階の微分方程式となりますね。
\ddot{x}(t)=-\frac{k}{m}x(t)=-\omega^2 x(t)
\end{align}
ここで\(\omega=\sqrt{k/m}\)とおきました。初期条件は以下のようになります。
x(0)=-d\\
\dot{x}(0)=0
\end{cases}\end{align}
この初期条件の元に2階の微分方程式を解いてみましょう。解は次の形になることがわかっています。
x(t)=A\sin\omega t+B\cos\omega t
\end{align}
ここに初期条件をいれていきましょう。
x(0)=B=-d
\end{align}
また、
\dot{x}(0)=A\omega=0\Longleftrightarrow A=0
\end{align}
なので、以下のように解が求まりました。
x(t)=-d\cos\omega t
\end{align}
\(\cos\)の中身の\(\omega t\)が\(0\to2\pi\)と変化するとまた元の状態になって同じ運動を繰り返します。ですので、時間\(t\)を基準に考えると、
T=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{m}{k}}
\end{align}
がこの運動の周期となります。今回の場合は質点の質量\(m\)が大きいと周期が長くなります。また、ばねが強ければ(すなわちが\(k\)大きければ)周期は短くなります。定性的なイメージとも一致するはずです。
重いものがくっついてたら、ゆっくり振動しそうだし、ばねが強ければ、ビュンビュン振動しそうじゃないですか。
今回、単振動は\(x=0\)を中心に、\(-d\leq x\leq d\)の幅を動くので、\(d\)のことを振幅と言います。
ここまでが単振動のもっとも基本的な説明です。基本的には、運動方程式を
\ddot{x}(t)=-\omega^2 x(t)
\end{align}
の形に持っていけるなら、それは単振動を表しています。初期条件によっては\(\sin\)と\(\cos\)の両方が入ったものが解になりますが、いずれにしても周期は\(2\pi/\omega\)になります。
また、初期条件によって、振幅も変わりますが、基本的には
-d\leq x-\alpha\leq d
\end{align}
の形に収まり、\(d\)を振幅と言うことができます。このとき中心の位置は\(x=\alpha\)です。
公式
運動方程式によってある物体の位置の時間変化が以下のように表されるとき、
\ddot{x}(t)=-\omega^2 x(t)
\end{align}
その物体は単振動する。\(\omega\)のことを角速度と言い、この単振動の周期\(T\)は角振動数を用いて以下のように表される。
T=\frac{2\pi}{\omega}
\end{align}
運動方程式は必ず、
x(t)=A\sin\omega t+B\cos\omega t
\end{align}
の形になり、この\(A\)と\(B\)は初期条件によって決まる。方程式を初期条件を用いて解いた結果、物体の移動範囲が
-d\leq x-\alpha\leq d
\end{align}
となるとき、\(d\)のことを振幅と言い、\(x=\alpha\)を振動の中心と言う。
1つ例を見たくらいではいまいち掴みきれないでしょうから2つほど問題を扱っておきましょう。
問題
以下のように密度\(\rho_0\)の液体を張った水槽に質量\(m\)、1辺の長さ\(l\)の立方体を浮かせる。このとき、立方体の底から\(l_0\)だけ沈んだところで立方体は静止した。
この状態から、立方体を\(x_0\)だけさらに押し沈めて手を離すと立方体が単振動することを示せ。また、運動方程式を解け。
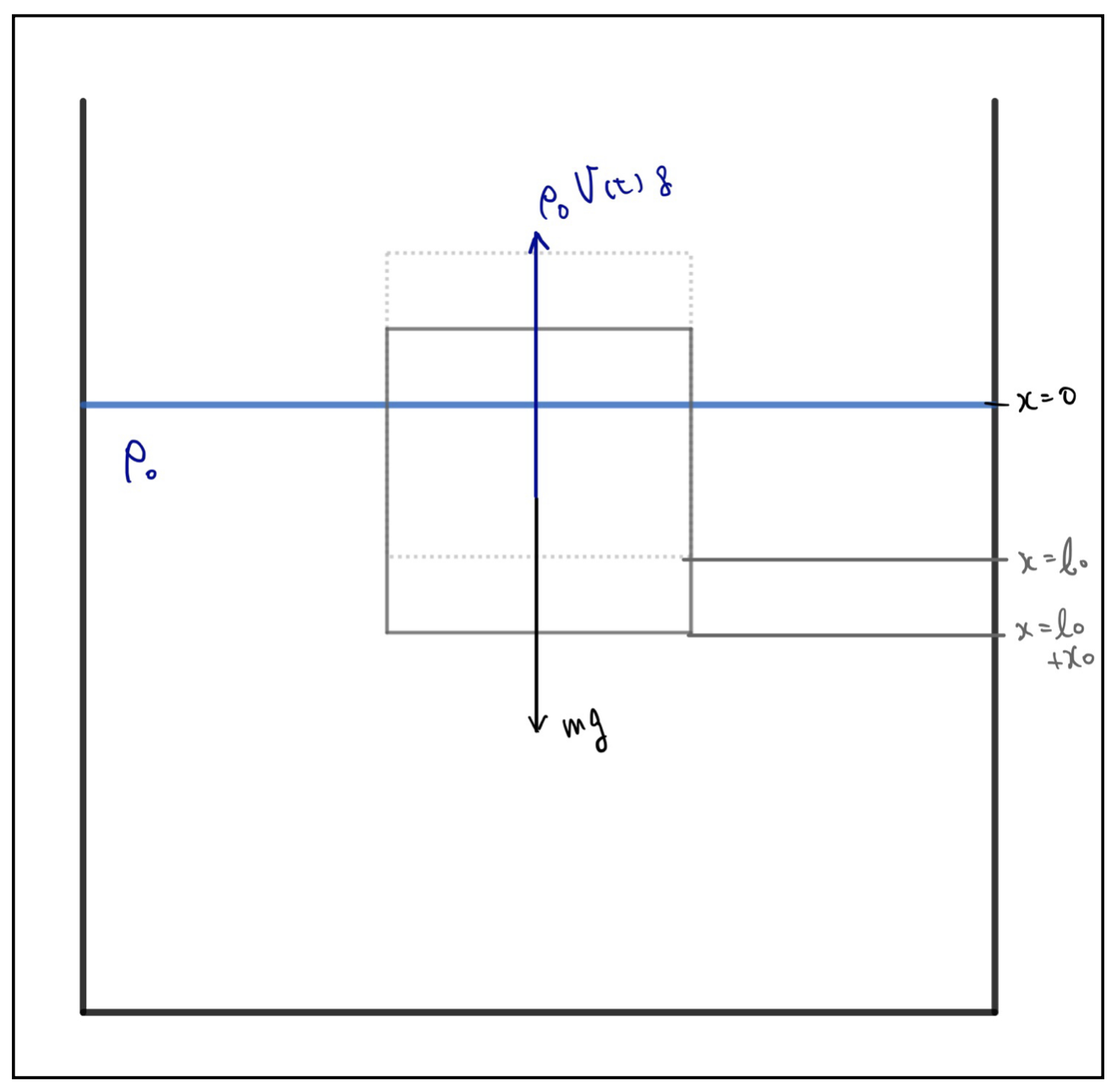
解答
まず、液体に沈んでいる分の体積\(V(t)\)を計算しましょう。その体積に浮力は比例しますからね。液面を\(x=0\)とし、そこから下向きに立方体の底面がどれだけ沈んでいるかと言う向きに\(x(t)\)を測ることにすると、
V(t)=l^2 x(t)
\end{align}
となります。下向きを正にしているということも注意してくださいね。浮力は上向きなので、運動方程式は以下のように書けます。
&m\ddot{x}(t)=mg-\rho_0l^2x(t)g\\
\Longleftrightarrow
&\ddot{x}(t)=-\frac{\rho_0l^2g}{m}\left(x(t)-\frac{m}{\rho_0l^2}\right)
\end{align}
この形は正に単振動をする運動方程式の形、とは見えないかもしれませんが、実はこれも単振動をする運動方程式の形です。右辺のカッコでくくったところを時間で2階微分すると左辺になりますからね。わざわざ真面目に書くとするなら、
\frac{d^2}{dt^2}\left(x(t)-\frac{m}{\rho_0l^2}\right)=-\frac{\rho_0l^2g}{m}\left(x(t)-\frac{m}{\rho_0l^2}\right)
\end{align}
として、このかっこの部分を改めて\(x'(t)\)と置き直してみましょう。すると、
\ddot{x’}(t)=-\frac{\rho_0l^2g}{m}x'(t)
\end{align}
と書けます。この解はいつもの形ですので、
x'(t)=A\sin \omega t+B\cos\omega t
\end{align}
となるわけですが、位置の関数を取り直したので、初期条件には注意が必要です。
x'(0)=x(0)-\frac{m}{\rho_0l^2}=x_0+l_0-\frac{m}{\rho_0l^2}=B\\
\dot{x'(0)}=\dot{x}(0)=0=A\omega\Longleftrightarrow A=0
\end{cases}\end{align}
となります。ここで、\(m/\rho_0l^2\)について考えてみましょう。これはつりあいの位置について考えることがコツです。
はじめに立方体が静止したときには以下のつりあいの式が成り立っています。それを変形すると、
mg=\rho_0l^2l_0g\Longleftrightarrow l_0=\frac{m}{\rho_0l^2}
\end{align}
これを\(B\)の式に代入し、\(x'(t)\)ではなくを\(x(t)\)用いて運動方程式の解を表現すると以下のようになります。
x(t)=l_0+x_0\cos\omega t
\end{align}
この形になると、\(x(t)\)は\(l_0\)を中心に、振幅\(x_0\)で振動することがわかりますね。振動の中心はつりあいの位置になっているということです。
もちろん\(\omega\)は以下の形ですよ。
\omega=\sqrt{\frac{\rho_0l^2g}{m}}
\end{align}
ちなみにこの単振動の1周期の中で1番速さが大きいのはどの瞬間か予想できますか?実際に考えてみましょう。
&\dot{x}(t)=-x_0\omega \sin \omega t\\
\Longleftrightarrow
&\left|\dot{x}(t)\right|\leq x_0\omega
\end{align}
ですね。
絶対値の記号は覚えていますか?それからは\(\sin\)単位円周上の\(y\)座標なのですから、\(\pm1\)の幅に収りますね。これらを合わせると上のように最高速が求められます。
単振動の最高速は振幅と角速度のかけ算になります。
最後に振れ幅が小さいときの振り子の運動が単振動とみなせることを見て単振動の節は終わることとしましょう。
例
以下の図のように天井から軽くて伸び縮みしない長さ\(l\)の糸を用いて質点をぶら下げた。静止している質点にある瞬間に水平方向に\(v_0\)の速度を与えると、振り子が微小角度の単振動を始めた。周期を求めよ。
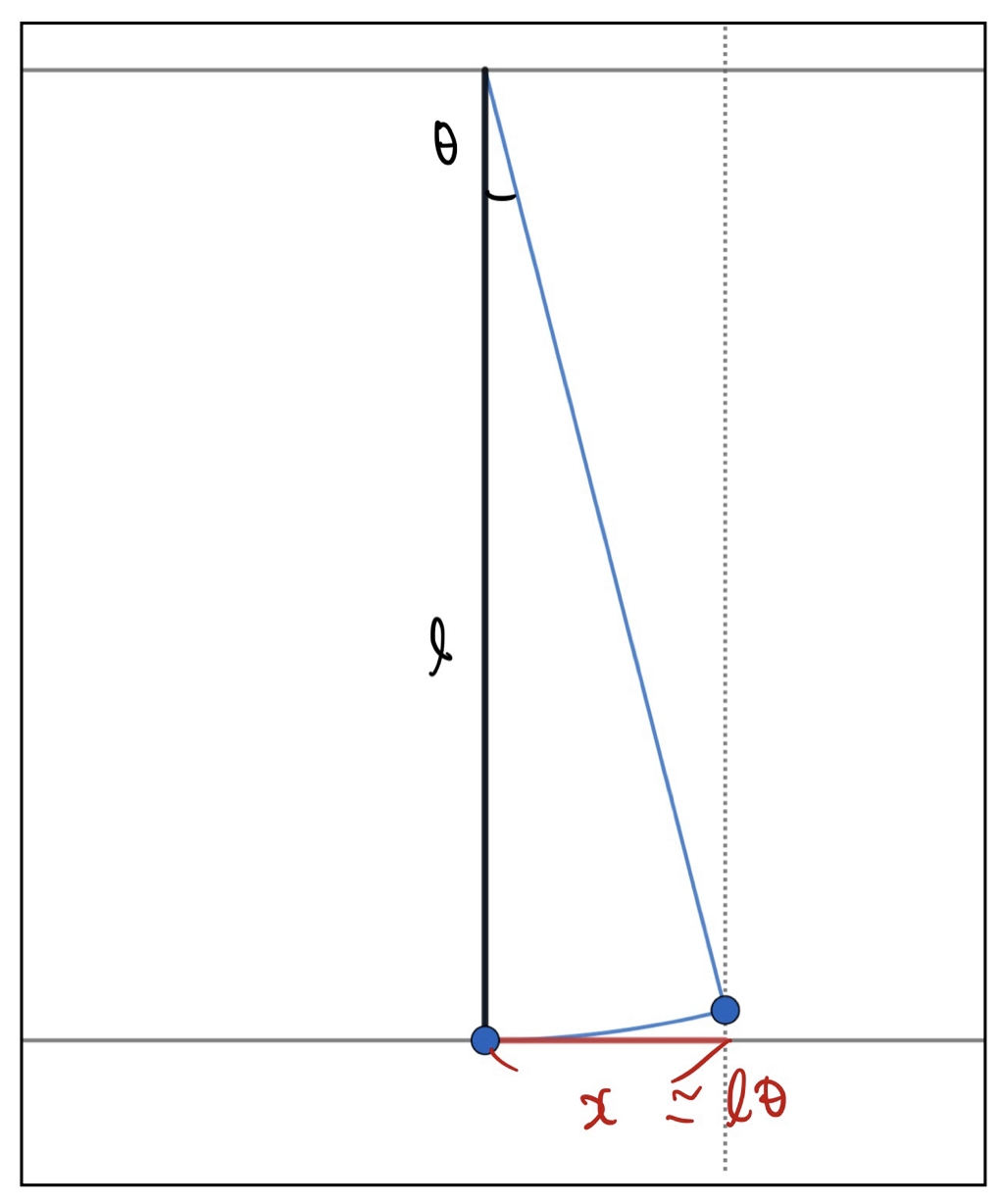
まずは図を見ていただきましょう。
質点が図のように角度\(\theta\)のところにいるときには、糸の方向と垂直な方向に\(mg\sin\theta\)の力を受けます。(ここまで勉強してきていたら、自分で図を描けるはずです。)
糸の方向については糸の長さが変わらないことからつりあいの関係にあることを意識しておいてください。
ここで、図のおうぎ形の弧の長さは\(\theta\)が小さいときには、赤線で示した部分の長さに近似できます。赤線の長さが\(x\simeq l\theta\)とおけるというわけですね。
この赤線を質点の変位と近似すると以下のように運動方程式を近似できます。
m\ddot{x}(t)=-mg\sin\theta
\end{align}
この右辺を変形していきます。まず、三角関数の極限の公式から、
&\lim_{\theta\to0}\frac{\sin\theta}{\theta}=1\\
\rightarrow
&\sin\theta\simeq\theta(when\quad \theta<<1)
\end{align}
という近似ができます。さらにここに\(x\simeq l\theta\)を入れてやるわけです。そうすると、
&m\ddot{x}(t)=-mg\sin\theta\\
\Longleftrightarrow
&\ddot{x}(t)=-\frac{g}{l}x(t)
\end{align}
と運動方程式を書き直すことができます。これは単振動をするタイプの運動方程式になっていますね。
このとき、角速度は以下のようになりますね。
\omega=\sqrt{\frac{g}{l}}
\end{align}
ですので、周期は以下のように求められます。
T=2\pi\sqrt{\frac{l}{g}}
\end{align}
糸が長いと周期が長いということは小中学校でも習った内容ではないでしょうか。ちなみに、こんな簡単なセッティングの振り子でも微小幅の振動では無い場合にはもっとハードな数学の知識が必要になります。楕円関数というのですが、わたくしもまだ真面目に勉強したことがありません。。。
特別講座として、こちらに単振動関連の記事リンクを2つ貼っておきます。
全種類の方は摩擦による単振動はここまでの内容では扱えませんが、それ以外は現時点で理解できる構成になっていますので、どうぞ。
>>【単振動が難しいのは種類を知らないから】高校物理の単振動全7種類
>>2種類の力学的エネルギーの保存則の違いがわからない方へ
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」







