(※数式が見切れている場合は横スクロールしてください。)
さて、ここまでで時刻の関数になっているベクトルを時間微分したり、時間積分したりすることができるようになっているので、マキノさんは1次元の質点の運動から、2次元3次元の運動へとコマを進めることができるようになっています。
その流れの概観を簡単に説明したのちに、例題を確認して、どういったことが考えられるようになったのか理解していただければと思います。
まず、質量\(m\)の物体mにの力\(\vec{F}(t)\)が加わっている状況を考えます。初期条件さえ与えられば、運動方程式を解くことによって物体mの速度\(\vec{v}(t)\)などを得ることが出来ます。
以前の「位置、速度、加速度の関係1&2」では1次元上(直線上)の質点の動きのみを考えていたので、この時には「符号」さえ意識していればそれで向きを考慮していることになっていました。
例えば、マイナスの速度であれば数直線上を負の方向へ進んでいることがわかりますし、プラスでは正の方向へと進んでいることがわかりますよね。
ベクトルという概念を勉強したので、今度は、1次元に運動を限定する必要はなくなりました。普段見慣れているこの世界はほとんどの方にとっては3次元に見えているでしょうし、3次元上では、位置も速度も加速度もベクトルで表現するのが自然です。(位置に関しては、原点を任意に決めてそこからの距離と方向をベクトルで表していると考えます。)
3次元上でも運動方程式の形は同じで以下のようになります。
m\vec{a}(t)=\vec{F}(t)
\end{align}
これが、質点mにFという力がかかっているときの加速度と力の関係を表した運動方程式です。もちろんベクトルで表していても、位置、速度、加速度の関係は微分と積分でつなぐことができて、その関係は以下のようなものです
\vec{x}(t)\xrightarrow{時間微分}&\vec{v}(t)\xrightarrow{時間微分}\vec{a}(t)\\
\vec{x}(t)\xleftarrow{積分と初期条件}& \vec{v}(t)\xleftarrow{積分と初期条件}\vec{a}(t)
\end{align}
ここまでの基本的な考え方をもとに次の問題を考えてみましょう。
問題
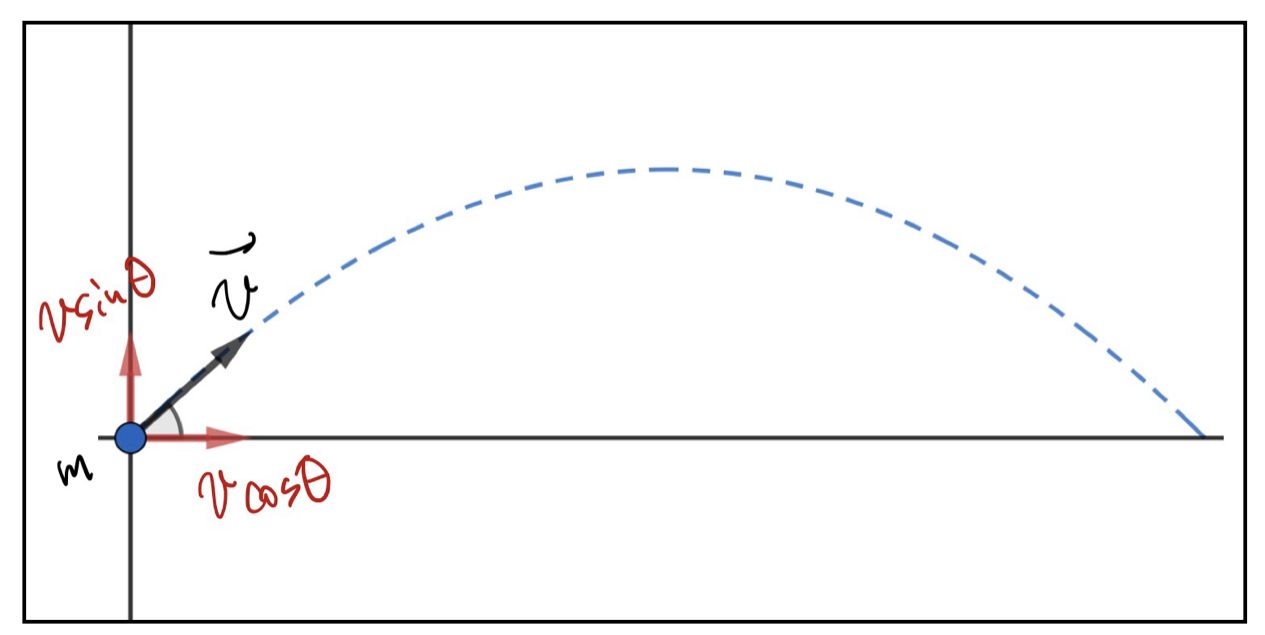
質点mの斜方投射を考える。時刻\(t=0\)において、質点mを水平線から角度\(\theta\)の方向へ速さ(=速度ベクトルの大きさ)\(v\)で投げ上げる。図参照。
このときに以下の問いに答えよ。
1.
初速度を表す速度ベクトルを2成分の成分表示にせよ。
2.
質点の運動方程式を立てて、それを解くことで質点の座標\((x,y)\)を時間の関数として表せ。
3.
最高到達点の高さを求めよ。
4.
着地地点の座標を答えよ。
5.
着地の瞬間の速度ベクトルを計算し、投げ上げた瞬間と同じ速さで着地することを確認せよ。
解答
1.
もう答えを書いてしまいましたけど、問題のところに与えた図からすぐに書けます。
\vec{v}(t=0)=\begin{pmatrix}v\cos\theta\\v\sin\theta\end{pmatrix}
\end{align}
2.
投げ上げた瞬間から着地するまでにかかる力は重力のみです。よって質点にかかるを2成分のベクトルで表すと、
\vec{F}(t)=\begin{pmatrix}0\\-mg\end{pmatrix}
\end{align}
プラスマイナスの符号をしっかり意識して書けるといいですね。
さてここで、力がベクトルで表現できたので、運動方程式は以下のようになります。
&m\vec{a}(t)=\vec{F}(t)=\begin{pmatrix}0\\-mg\end{pmatrix}\\
\Longleftrightarrow&\vec{a}(t)=\begin{pmatrix}0\\-g\end{pmatrix}
\end{align}
これを積分して解いて速度ベクトルを以下のように得ることができます。
\vec{v}(t)=&\vec{v}(0)+\int^t_0\vec{a}(t’)dt’\\
=&\begin{pmatrix}v\cos\theta\\v\sin\theta\end{pmatrix}+\begin{pmatrix}0\\-gt\end{pmatrix}\\
=&\begin{pmatrix}v\cos\theta\\v\sin\theta-gt\end{pmatrix}
\end{align}
運動方程式からも分かりますが、\(x\)方向には等速運動で、\(y\)軸方向には等加速度運動をしていることが分かります。
さらに積分することで位置ベクトルが以下のように得られますね。
\vec{x}(t)=&\vec{x}(0)+\int^t_0\vec{v}(t’)dt’\\
=&\begin{pmatrix}0\\0\end{pmatrix}+\begin{pmatrix}(v\cos\theta)t\\(v\sin\theta)t-\frac{1}{2}gt^2\end{pmatrix}\\
=&\begin{pmatrix}(v\cos\theta)t\\(v\sin\theta)t-\frac{1}{2}gt^2\end{pmatrix}
\end{align}
3.
最高到達点では速度の\(y\)成分がゼロになることが定性的に分かります。ちょっと難しいですかね?
\(y\)成分の速度は最初プラスです。そこから段々と小さくなっていくのは\(\vec{v}(t)\)の\(y\)成分の形を見るとわかりますね。プラスのうちはだんだんと上に進むわけですが、マイナスになってしまうと今度は下に進みだすわけですね。ということはその\(y\)成分がゼロになった瞬間が一番高いところです。
そこで、その瞬間の時刻を\(t’\)とすると
&\vec{v}(t’)=\begin{pmatrix}v\cos\theta\\v\sin\theta-gt’\end{pmatrix}=\begin{pmatrix}v\cos\theta\\0\end{pmatrix}\\
\Longleftrightarrow&t’=\frac{v\sin\theta}{g}
\end{align}
が分かります。この\(t’\)を位置ベクトル\(\vec{x}(t)\)に代入すれば、最高到達点の高さが以下のように分かります。
\vec{x}(t’)=&\begin{pmatrix}(v\cos\theta)\frac{v\sin\theta}{g}\\(v\sin\theta)\frac{v\sin\theta}{g}-\frac{1}{2}g\left(\frac{v\sin\theta}{g}\right)^2\end{pmatrix}\\
=&\begin{pmatrix}\frac{v^2\sin\theta\cos\theta}{g}\\\frac{v^2\sin^2\theta}{2g}\end{pmatrix}
\end{align}
この\(y\)成分が求める答えです。
4.
着地の瞬間というのを言い換えると、位置ベクトルの\(y\)成分がゼロになる瞬間です。この瞬間を\(t”\)とすると、
\vec{x}(t”)=\begin{pmatrix}(v\cos\theta)t”\\(v\sin\theta)t”-\frac{1}{2}gt”^2\end{pmatrix}=\begin{pmatrix}(v\cos\theta)t”\\0\end{pmatrix}
\end{align}
となります。この\(y\)成分に着目して\(t”\)について解くと
t”=\frac{2v\sin\theta}{g}
\end{align}
となります。これをもう一度、改めて位置ベクトルの\(x\)成分に入れると着地点の座標が分かるわけです。
\vec{x}(t”)=\begin{pmatrix}\frac{2v^2\sin\theta\cos\theta}{g}\\0\end{pmatrix}
\end{align}
5.
前の問題と同じ\(t”\)を速度ベクトルに入れてその大きさを計算すればよいですね。
\vec{v}(t”)=\begin{pmatrix}v\cos\theta\\v\sin\theta-g\frac{2v\sin\theta}{g}\end{pmatrix}=\begin{pmatrix}v\cos\theta\\-v\sin\theta\end{pmatrix}
\end{align}
着地の瞬間には\(y\)成分の符号が変わっただけなので、速度ベクトルの大きさは同じです。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」








