(※数式が見切れている場合は横スクロールしてください。)
この章は簡単な三角関数の公式の1つの紹介です。
ベクトルの内積を勉強したマキノさんにとってはかなりイージーな章になっています。
まずこちらの三角形をご覧ください。
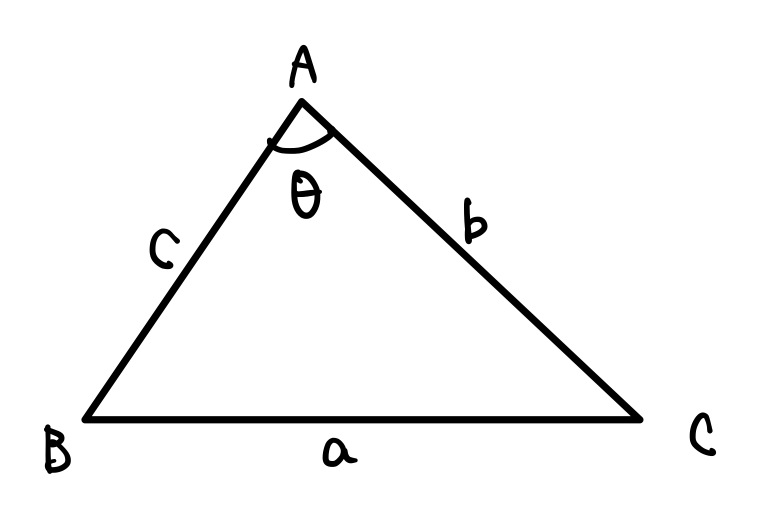
三角形ABCがあって、以下のように数値が与えられているとします。
\begin{align}\begin{cases}
AB=c\\
AC=b\\
\angle BAC=\theta
\end{cases}\end{align}
AB=c\\
AC=b\\
\angle BAC=\theta
\end{cases}\end{align}
これらの値を使って、\(BC\)の長さ\(a\)を求める公式を余弦定理と言います。
ベクトルで考えるとすぐに計算ができます。
\begin{align}
\left|\vec{BC}\right|^2=&\left|\vec{AC}-\vec{AB}\right|^2\\
=&\left|\vec{AC}\right|^2-2\vec{AC}\cdot\vec{AB}+\left|\vec{AB}\right|^2\\
=&b^2-2bc\cos\theta+c^2
\end{align}
\left|\vec{BC}\right|^2=&\left|\vec{AC}-\vec{AB}\right|^2\\
=&\left|\vec{AC}\right|^2-2\vec{AC}\cdot\vec{AB}+\left|\vec{AB}\right|^2\\
=&b^2-2bc\cos\theta+c^2
\end{align}
これのルートを取れば\(a\)が出ます。
以下を余弦定理という公式として覚えておくといいかと思います。
公式
以下の式を余弦定理という。
\begin{align}
a^2=b^2+c^2-2bc\cos\theta
\end{align}
a^2=b^2+c^2-2bc\cos\theta
\end{align}
問題
\(\angle B=\phi\)とするとき、\(b\)を\(\phi\)、\(a\)、\(c\)で表せ。
解答
やることは全く同じです。
\begin{align}
\left|\vec{AC}\right|^2=&\left|\vec{BC}-\vec{BA}\right|^2\\
=&\left|\vec{BC}\right|^2-2\vec{BC}\cdot\vec{BA}+\left|\vec{BA}\right|^2\\
=&a^2-2ac\cos\phi+c^2
\end{align}
\left|\vec{AC}\right|^2=&\left|\vec{BC}-\vec{BA}\right|^2\\
=&\left|\vec{BC}\right|^2-2\vec{BC}\cdot\vec{BA}+\left|\vec{BA}\right|^2\\
=&a^2-2ac\cos\phi+c^2
\end{align}
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」
スポンサーリンク
