媒介変数表示と軌跡｜ぽこラボ勉強ブログ

(※数式が見切れている場合は横スクロールしてください。)

またすぐに数学の章を挟むことになってしまいますが、今回は数学の中でも割と物理寄りの内容なので、マキノさんもいつもよりは気持ち的には楽に勉強できるかもしれません。

時刻の関数で表された以下のベクトルをまず例にとって考えてみます。質点の位置だと思ってください。

$\begin{align} \vec{x}(t)=\begin{pmatrix}x(t)\\y(t)\end{pmatrix}=\begin{pmatrix}t\\2t\end{pmatrix} \end{align}$

この $t$ に様々な値を代入していき、それをプロットしていくと、以下のような直線が現れます。

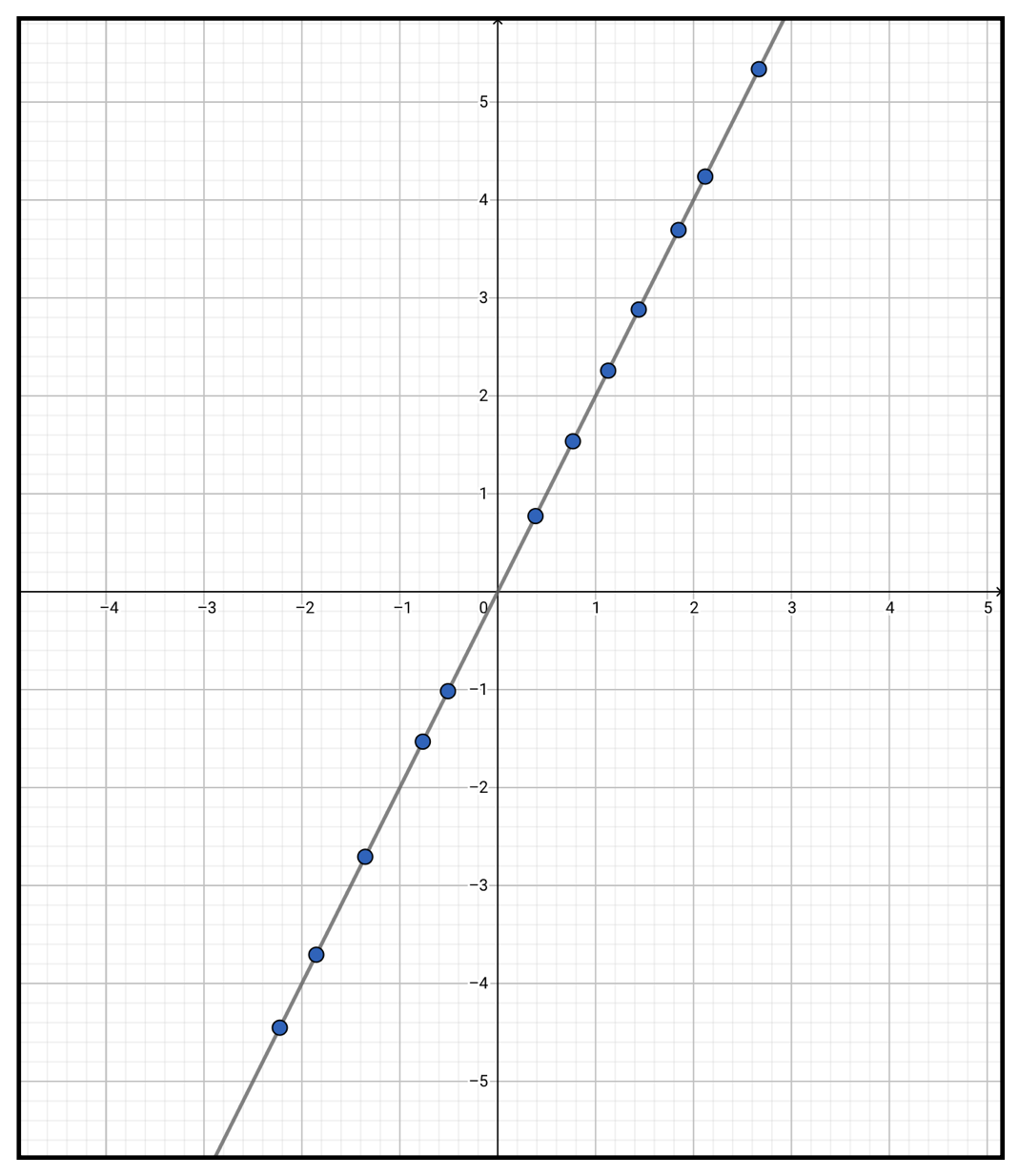
このように時刻などを媒介して、主に2次元以上の情報を表示する方法をと言い、その（今の例だと $t$ のこと）を様々な値に振り、描く図形を軌跡と言います。

基本的に高校数学の範囲だと、今の例のような位置を媒介変数で表して、その媒介変数表示で表される図形を求めるような例を習うことが多いです。

媒介変数表示から軌跡を導くには基本的には、媒介変数を消してやればいいです。今回の例だと、

$\begin{align} \begin{cases} x=t\\ y=2t \end{cases}\Longrightarrow\quad y=2x \end{align}$

という風に連立して $t$ を消してやると、軌跡として直線の式が出てきます。ただし、この右と左で同じだけの情報量を持っているということはできません。

左側は各時刻での質点の位置や、速度を知ることができますが、軌跡の形にしてしまうと、各時刻での位置や速度の情報は落ちてしまいます。

問題

各時刻の質点の位置が以下のベクトルで表されているとする。

$\begin{align} \vec{x}(t)=\begin{pmatrix}x(t)\\y(t)\end{pmatrix}=\begin{pmatrix}t\\2t^2\end{pmatrix} \end{align}$

このとき、各時刻の質点の速度、加速度を求めよ。また、この質点が描く軌跡を求めよ。

解答

それほど、難しい問題ではないと思います。

まず、速度と加速度は微分をすれば出てきますね。

$\begin{align} \begin{cases} \vec{v}(t)=\dot{\vec{x}}(t)=\begin{pmatrix}1\\4t\end{pmatrix}\\ \vec{a}(t)=\ddot{\vec{x}}(t)=\begin{pmatrix}0\\4\end{pmatrix} \end{cases} \end{align}$

これで終わりです。そして、軌跡ですが、以下のようにすればいいだけです。

$\begin{align} y=2t^2=2x^2 \end{align}$

結局放物線が得られるということですね。

この軌跡を満たす媒介変数表示は他にいくらでも作れて、例えば、

$\begin{align} \vec{x}(t)=\begin{pmatrix}2t\\8t^2\end{pmatrix} \end{align}$

でも同じ軌跡が得られます。これだと問題とは異なる速度や加速度が得られるわけですね。ですから、軌跡を最初から与えるよりも媒介変数表示の方が情報量は多くなっているわけです。

関連リンク

>>ブログ版アラサー高校物理の記事一覧

>>物理の勉強ロードマップ【2019年版】

>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」

東大理系攻略法

東大卒の現役塾講師が
東大理系攻略法を
解説したPDF販売中！

中高一貫校に行かなくても、塾に行かなくても、独学で受かるための勉強法を完全解説！

全科目の参考書
全参考書の使い方
受験までの勉強スケジュール
が全てわかります！

今だけ！100様限定60%OFF！
さらに24時間以内なら返金保証つき！

会員数500万人超の「note」で
無料サンプル公開！

無料サンプル
を見る≫

合成関数

【教え方の教科書】授業の考え方

ベクトルの定数倍