(※数式が見切れている場合は横スクロールしてください。)
今度はベクトルの外積という計算を勉強していきます。内積というのは以前勉強しましたね。ちゃんと覚えていますかマキノさん?覚えていなければ、以前の章に戻って勉強してから改めてこの章の勉強を始めていきましょう。
ベクトルの外積は2つのベクトルを元にして1つの新たなベクトルを作るルールのことです。以下の図を見てください。
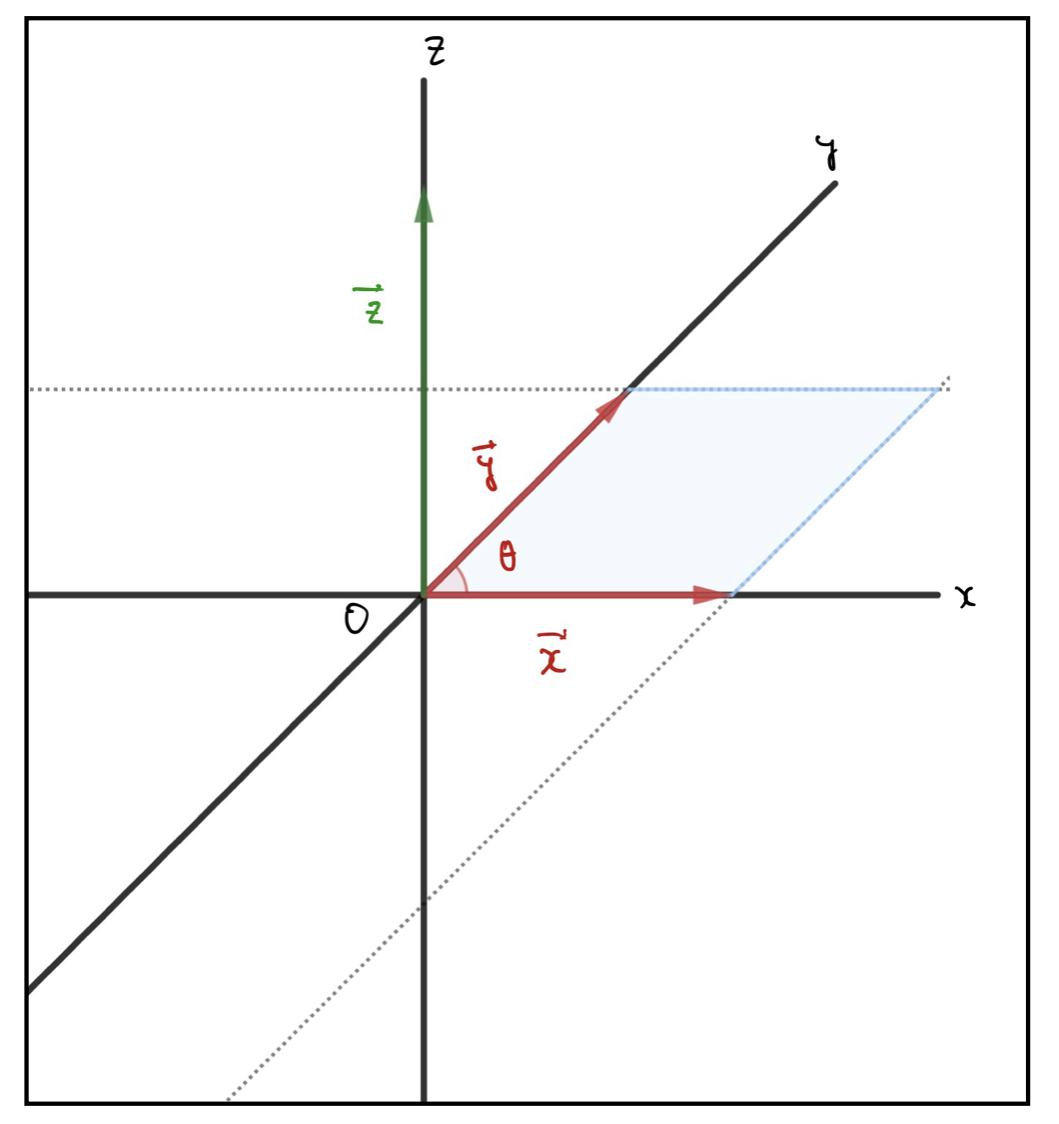
3次元空間に\(\vec{x}\)と\(\vec{y}\)があり、これを元にして作られた\(\vec{z}\)があります。まず外積の書き方ですが、以下のように書きます。
\vec{z}=\vec{x}\times\vec{y}
\end{align}
ベクトルの外積を表す場合にはこのかけ算記号は省略できません。\(\vec{z}\)をただ1つ定めるには、大きさと向きを決めなければなりません。まず大きさは以下のルールで決めます。
\left|\vec{z}\right|=\left|\vec{x}\right|\cdot\left|\vec{y}\right|\sin\theta
\end{align}
つまりの大きさは\(\vec{x}\)の大きさと\(\vec{y}\)の大きさとそれらのなす角\(\theta\)の\(\sin\)のかけ算で決まるということです。図で示した平行四辺形の面積の大きさが\(\vec{z}\)の大きさです。(面積が長さに対応しているのを不思議に思ったなら中々するどいのですが、ここでは解説をしないことにします。)
次に向きです。まず\(\vec{x}\)と\(\vec{y}\)の両方を含む面はただ1つに決まりますね。先程の図でいうと、\(xy\)平面です。(別にこんなにきれいに収まるように直行座標を用意する必要はないのですが。)
先ほど定義した大きさで、その面に垂直な方向に向くベクトルは2種類作れます。このうち右ねじの法則を満たす方が外積の定義として一般的なものです。
右ねじをもっと真面目に説明しましょう。
\(\vec{z}\)がネジだとしたときに、\(\vec{x}\)から\(\vec{y}\)の方向へネジを回すとネジが進む方向が\(\vec{z}\)の正しい向きです。
うーん、これでもあんまりわかりやすくないですよね笑
違う言い方をします。右手を用意していただいて、親指を\(\vec{x}\)に合わせてください。人差し指を\(\vec{y}\)にしてください。そしたら、中指を親指とも人差し指とも垂直な方向に曲げられますよね。それが\(\vec{z}\)の方向です。
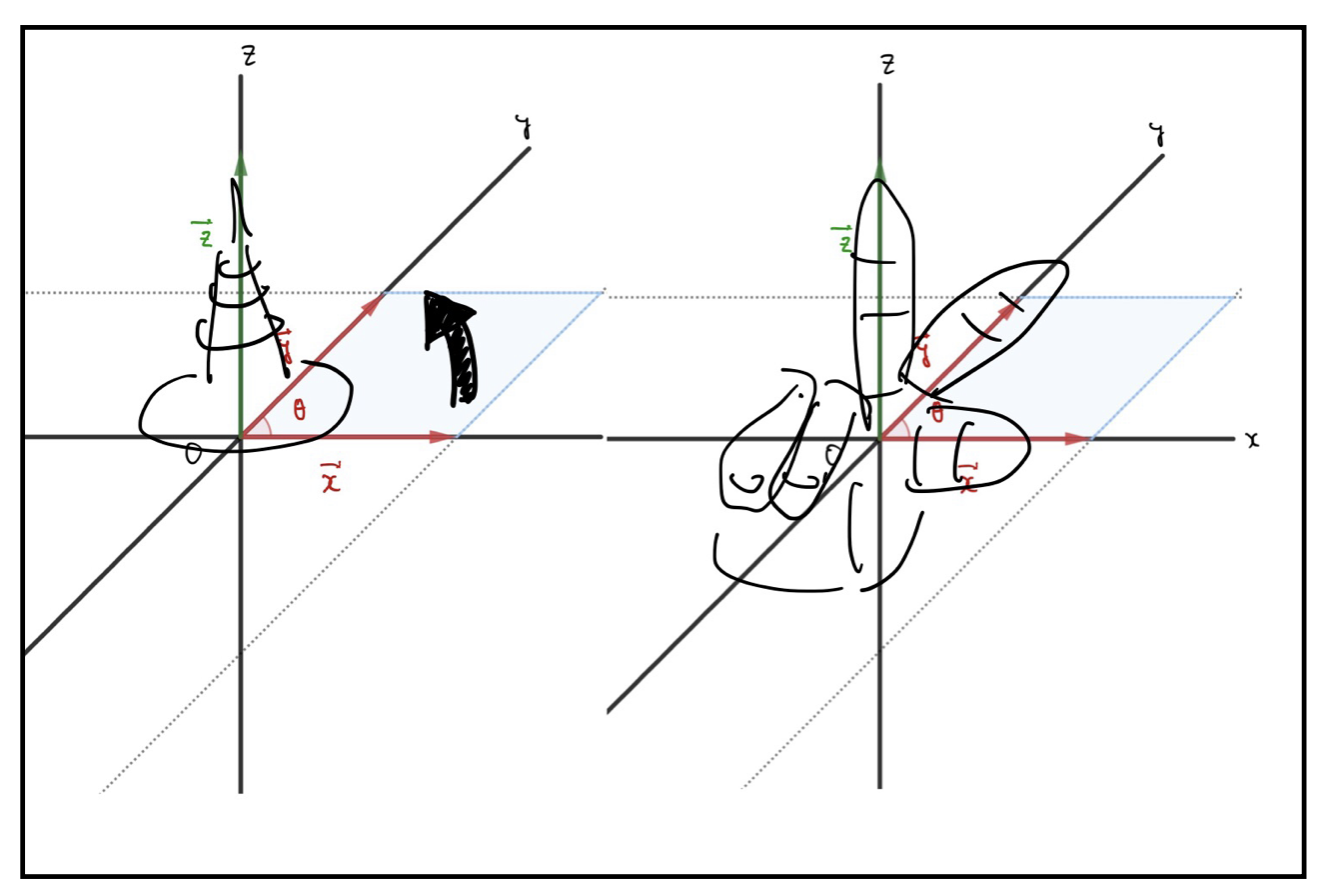
はい、もう少し絵心のある絵を探してください笑
なんにせよ、これで外積が定義できたことにします。
定義
\(\vec{x}\)と\(\vec{y}\)でできる外積
\vec{z}=\vec{x}\times\vec{y}
\end{align}
は右ねじの法則を満たす向きで定義し、その大きさは以下のように決める。
\left|\vec{z}\right|=\left|\vec{x}\right|\cdot\left|\vec{y}\right|\sin\theta
\end{align}
ここで\(\theta\)は\(\vec{x}\)を\(\vec{y}\)に合わせるまで回転させたときの角度です。
問題
\vec{a}=\begin{pmatrix}1\\0\\0\end{pmatrix},\quad\vec{b}=\begin{pmatrix}1\\1\\0\end{pmatrix}
\end{align}
と与えられた時、\(\vec{c}=\vec{a}\times\vec{b}\)を求めよ。
解答
まずは以下の図を見てください。
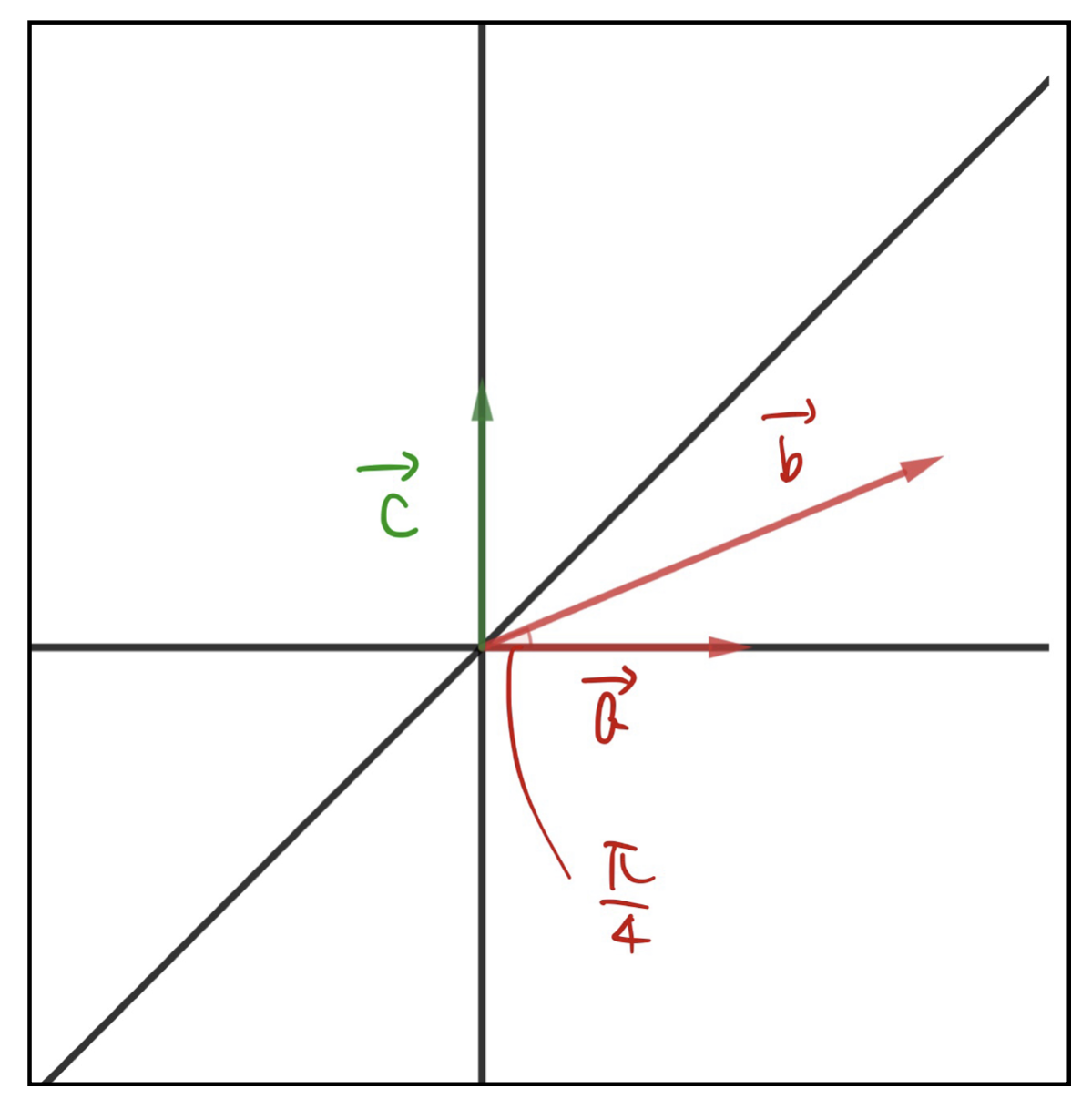
だいたいこんな感じになります。
まず\(\vec{c}\)の向きですけど、先ほどの例と同じく\(z\)軸方向に向きます。次に大きさは以下のように計算できます。
\left|\vec{c}\right|=&\left|\vec{a}\right|\cdot\left|\vec{b}\right|\sin\frac{\pi}{4}\\
=&1\cdot\sqrt{2}\cdot\frac{1}{\sqrt{2}}=1
\end{align}
よって、\(\vec{c}\)は
\vec{c}=\begin{pmatrix}0\\0\\1\end{pmatrix}
\end{align}
と決まります。
さて、これくらいの問題ならすぐに向きも決まりますし、大きさも決まるのですが、もっと面倒な関係にある2つのベクトルでも計算できるように準備していきましょう。
まずは、以下の問題を解いてみてください。
問題
以下の3つの単位ベクトルが与えられている。
&\vec{e_x}=\begin{pmatrix}1\\0\\0\end{pmatrix}\\
&\vec{e_y}=\begin{pmatrix}0\\1\\0\end{pmatrix}\\
&\vec{e_z}=\begin{pmatrix}0\\0\\1\end{pmatrix}
\end{align}
このとき、\(\vec{e_x}\times\vec{e_y}\)、\(\vec{e_y}\times\vec{e_z}\)、\(\vec{e_z}\times\vec{e_x}\)をそれぞれ求めよ。
解答
わりと簡単に計算できてしまいます。最初の\(\vec{e_x}\times\vec{e_y}\)に関しては、\(x\)軸方向を向く単位ベクトルと、\(y\)軸方向を向く単位ベクトルなので、これの外積の向く方向は\(z\)軸方向となります。
そして、この2つのベクトルが直行することと、大きさがそれぞれ\(1\)であることから、外積も単位ベクトルになります。すなわち、
\vec{e_x}\times\vec{e_y}=\vec{e_z}
\end{align}
ということです。あとは、添字を対称的に回すだけで答えが得られます。
&\vec{e_x}\times\vec{e_y}=\vec{e_z}\\
&\vec{e_y}\times\vec{e_z}=\vec{e_x}\\
&\vec{e_z}\times\vec{e_x}=\vec{e_y}
\end{align}
ちなみに同じベクトル同士の外積はどうなるのか。2つのベクトルがなす角が\(0\)なので、\(\sin 0=0\)から、ゼロになることがわかります。ただし、少し注意が必要なのは、外積はあくまでもベクトルなので、ゼロはゼロでも零ベクトルが同じベクトルの外積になります。
\vec{x}\times\vec{x}=\vec{0}
\end{align}
このゼロの上のベクトルを表す矢印は忘れてはいけません。
さて、この同じベクトル同士の外積、そして単位ベクトル同士の外積、さらに以下の分配法則を用いると、一般的なベクトル同士の外積が計算できるようになります。
定義
ベクトルの外積には以下のような分配法則が成り立つ。
&\left(A\vec{a}+B\vec{b}\right)\times\left(C\vec{c}+D\vec{d}\right)\\
=&AC\vec{a}\times\vec{b}+BC\vec{b}\times\vec{b}+AD\vec{a}\times\vec{d}+BD\vec{b}\times\vec{d}
\end{align}
では、これを使って以下の問題に挑戦してみましょう。
問題
次の公式を導出せよ。
\vec{x}=\begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix},\quad\vec{y}=\begin{pmatrix}y_1\\y_2\\y_3\end{pmatrix}
\end{align}
と与えられているとき、
\vec{x}\times\vec{y}=\begin{pmatrix}x_2y_3-y_2x_3\\x_3y_1-y_3x_1\\x_1y_2-y_1x_2\end{pmatrix}
\end{align}
解答
内積のときも単位ベクトルを使って分解して内積を取る作業を通して公式を導出していましたが、あれとやるべきことは全く同じです。まず、以下のように単位ベクトルを使って分解します。
\vec{x}=x_1\vec{e_x}+x_2\vec{e_y}+x_3\vec{e_z}\\
\vec{y}=y_1\vec{e_x}+y_2\vec{e_y}+y_3\vec{e_z}
\end{cases}\end{align}
これらの外積を分配法則と単位ベクトルの外積の計算結果を使って、計算するだけです。
\vec{x}\times\vec{y}=x_1y_1\vec{e_x}\times\vec{e_x}+\cdots+x_3y_3\vec{e_z}\times\vec{e_z}
\end{align}
この右辺のうち、残る項は違う単位ベクトル同士の外積になっているものです。また、以下のように外積は順序を入れ替えると符号が変わります。
\vec{e_x}\times\vec{e_y}=-\vec{e_y}\times\vec{e_x}
\end{align}
なぜなら外積は右ねじの法則で向きが決まり、順番が入れ替わるとねじを回す向きが逆向きになるからですね。というわけで、先ほどの外積の右辺は以下のようになります。
\vec{x}\times\vec{y}=&(x_2y_3-x_3y_2)\vec{e_x}\\
+&(x_3y_1-x_1y_3)\vec{e_y}\\
+&(x_1y_2-x_2y_1)\vec{e_z}\\
\end{align}
これは導出したかった式そのものになっています。
それではこの公式に慣れておくために問題を解いておきましょう。
問題
以下のように\(\vec{a}\)と\(\vec{b}\)が与えられているとき、\(\vec{a}\times\vec{b}\)を計算せよ。
1.
\vec{a}=\begin{pmatrix}1\\2\\3\end{pmatrix},\quad\vec{b}=\begin{pmatrix}-3\\-2\\-1\end{pmatrix}
\end{align}
2.
\vec{a}=\begin{pmatrix}r\cos\omega t\\r\sin\omega t\\0\end{pmatrix},\quad\vec{b}=\begin{pmatrix}-r\omega\sin\omega t\\r\omega\cos\omega t\\0\end{pmatrix}
\end{align}
解答
1.
公式通りに計算するだけです。
\vec{a}\times\vec{b}=\begin{pmatrix}2\cdot(-1)-(-2)\cdot3\\
3\cdot(-3)-(-1)\cdot1\\
1\cdot(-2)-(-3)\cdot2\end{pmatrix}
=\begin{pmatrix}4\\-8\\4\end{pmatrix}
\end{align}
2.
意味深な数字に見えますかね?\(\vec{a}\)は\(xy\)平面上を円運動している質点の位置ベクトル、\(\vec{b}\)はその速度ベクトルを意識しています。が、ここでは普通に計算するだけです。
&\vec{a}\times\vec{b}\\
=&\begin{pmatrix}r\sin\omega t\cdot0-r\omega\cos\omega t\cdot0\\
0\cdot(-r\omega \sin\omega t)-0\cdot r\cos\omega t\\
r\cos\omega t\cdot r\omega \cos\omega t-(-r\omega \sin\omega t)\cdot r\sin\omega t\end{pmatrix}=\begin{pmatrix}0\\0\\r^2\omega\end{pmatrix}
\end{align}
この量に質量をかけると角運動量という量になります。すぐあとに出てきます。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」








