(※数式が見切れている場合は横スクロールしてください。)
ケプラーの第1法則を導いた結果として、力学的エネルギー\(E\)が負のときに、惑星が太陽を焦点とするだ円軌道を描くことがわかりました。
今回はこの力学的エネルギーが負の状態に関して考えてみましょう。
ここでも質量\(M\)の太陽を焦点として、だ円軌道を運動している質量\(m\)の惑星を考えることにしましょう。
ある時刻\(t\)において、惑星の速さが\(v\)で、惑星と太陽の距離が\(r\)だとしましょう。
このとき、惑星が持つ力学的エネルギー\(E\)は
E=\frac{mv^2}{2}-\frac{mMG}{r}
\end{align}
であり、これが負の状態というわけです。さて、これを\(v^2\)について解いてみましょう。
&\frac{mv^2}{2}=E+\frac{mMG}{r}\\
\Longleftrightarrow
&v^2=\frac{2E}{m}+\frac{2MG}{r}
\end{align}
これをグラフで描いて考察を進めてみましょう。
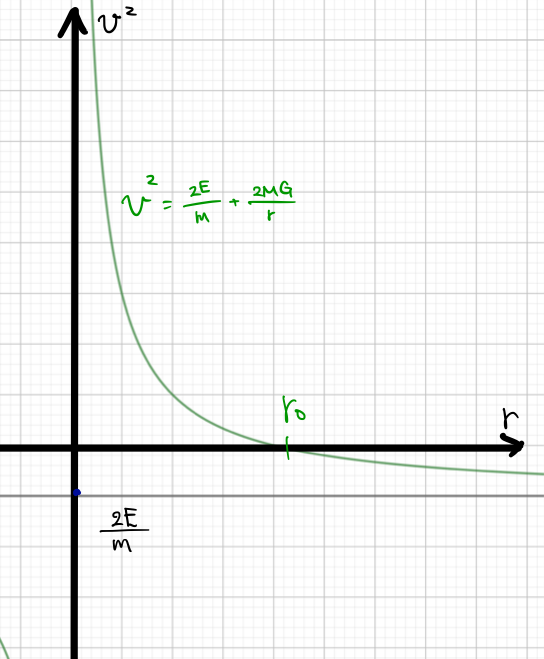
反比例のグラフを下に平行移動したものと考えればグラフを描けるはずです。
下になるのは\(E<0\)だからです。
縦軸は\(v^2\)にしましたが、\(v^2\)はいつでも正の値でないとおかしいので、グラフとしては\(r\)軸より上の部分しか物理的に対応する状態はあり得ません。
このとき、\(r\)には必ず最大値\(r_0\)があります。
これを言い換えると、\(E<0\)のときには太陽から惑星までの距離は\(r_0\)以上に離れることはできないということです。
これは惑星が太陽に束縛されているという状態です。
ちなみに\(E\geq0\)のときにはこういった最大値\(r_0\)は存在しないので、惑星は太陽から無限(\(r=\infty\))に離れることも可能です。
束縛状態という考え方は(ずいぶん後になりますが)、量子力学まで勉強を進めるとすごく重要な考え方であることがわかります。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」









