(※数式が見切れている場合は横スクロールしてください。)
さてさてマキノさん、ようやくベクトルという単元まで話が進みました。今回の数学準備はこのベクトルを説明するためだけにあったと言っても過言ではありません。ここを理解することで、今まで1次元で説明していた力学を3次元へ拡張することができるようになります。
ちなみにベクトルは高校生の多くがつまずく単元の１つです。とはいえ、大学受験のような面倒な内容はここには含まれていませんので、気楽に読み進めていただければと思います。
そもそもベクトルとは何か。そこからですね。
ベクトルとは「大きさ」（もしくは「長さ」ともいう）と、「向き」をの情報を持った数学的な構造物である、というのが一番自然な表現ですけど、数学的な構造物と言われてもって感じですよね？
もっと抽象的な定義もありますが、今は一旦、大きさと向きを指定すれば一つベクトルが指定できるというくらいの理解で大丈夫です。
初等的な数学の範囲では矢印で図示できるものと捉えてもらっても問題ありません。矢印は大きさと向きの情報を与えると表現できるものですもんね。
ベクトルって数学的構造物とはいうものの、ここまで習ってきた関数なんかよりもよっぽど目に触れる機会は多いんですよ。ベクトルを探すためには普段矢印で表現しているものを探せばいいんです。
世の中で矢印を使って表現すると都合のいいものは豊富にあって、例えば、天気図などで見る風の情報は矢印で書かれていますよね？
風の強さを「矢印の大きさ」で表現し、風向きを「矢印の向き」で表現すれば、それは十分ベクトルとしての性質を持つわけです。
他にも色々ありますけど、早速力学に入るとしましょう。
この章でお話したいベクトルで表現するものは「力」です。
このテキストの中では力は、加速度の源として初めてでてきました。その力というのはベクトルで表現すべきものなんです。
力はどの「向き」にどの「大きさ」で働いているかが分かって、情報として意味を持ちますもんね。これは常識的にそうだと理解できるでしょう。
向きと大きさの情報で記述できるものはベクトルで表現するのが都合がいいんです。そして、ベクトルの表現はこれ以降基本的には矢印を使います。
矢印には始点と終点があって、矢印はそれらをつなぐように描かれますよね。ベクトルも始点と終点が決まれば、大きさと向きの両方が決まるので、始点と終点を決めてやって書くことがあります。
例えば、始点をA、終点をBとするベクトルは
\vec{AB}
\end{align}
のようにABの上に右向き矢印を書いて表現します。そして、「ベクトルAB」と読みます。
このベクトルを矢印で図示すると以下のようなものになります。
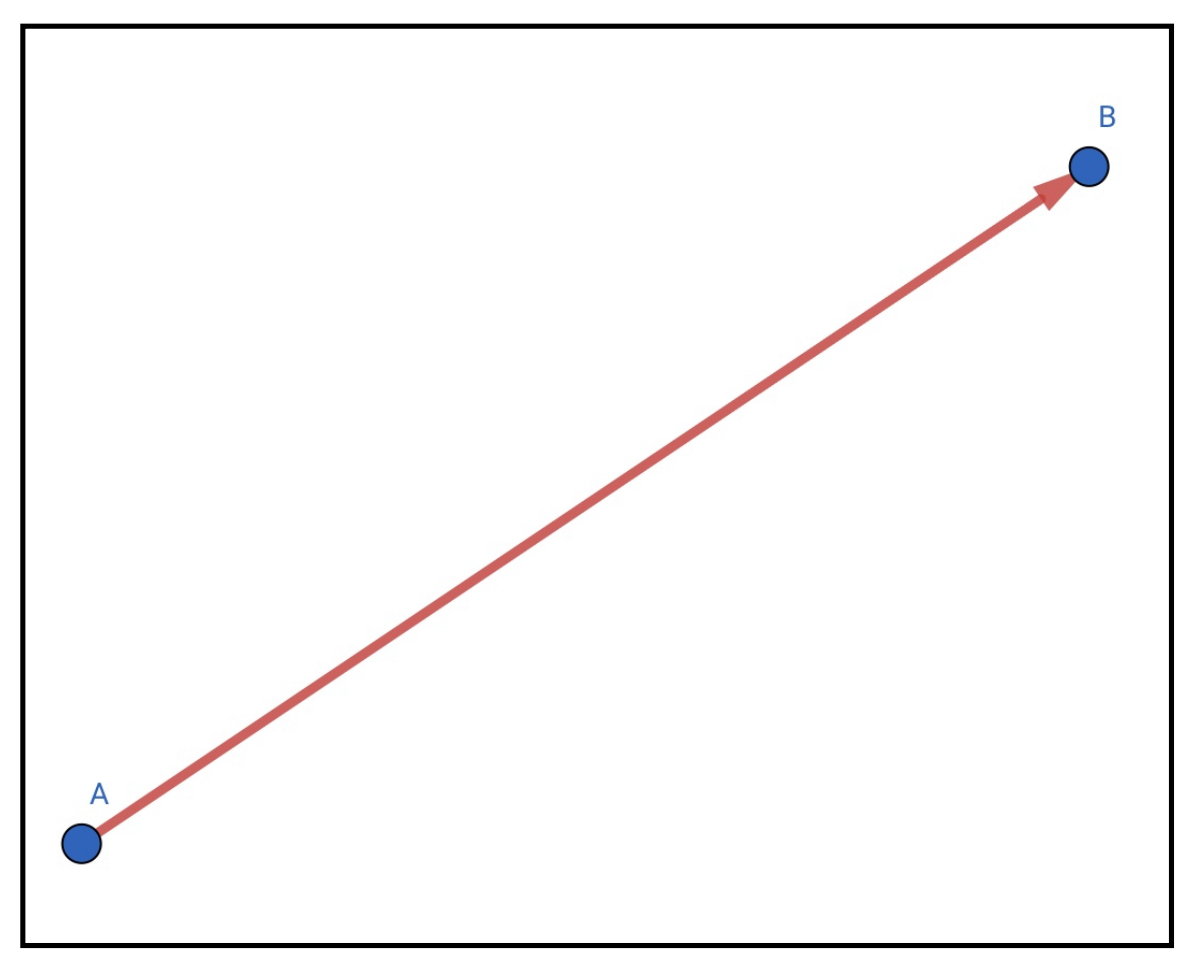
この矢印の長さがベクトルの大きさに対応していて、矢印の向きがベクトルの向きに対応しているわけです。
必ずしも、始点と終点を明記する必要はなくて、先程の図のベクトルABに改めてベクトルxという風に名前をつけてもよいです。その場合にも同じように
\vec{x}
\end{align}
という風に表現します。
ベクトルが2つあって、その向きと大きさが等しい場合にはそのベクトルの間を等号で結んで以下のように表現することができます。
\vec{x}=\vec{y}
\end{align}
ベクトルを等号でつなぐという作業に慣れておきましょう。
例
例えば平行四辺形ABCDを準備して、その各辺にベクトルを置いたとする。
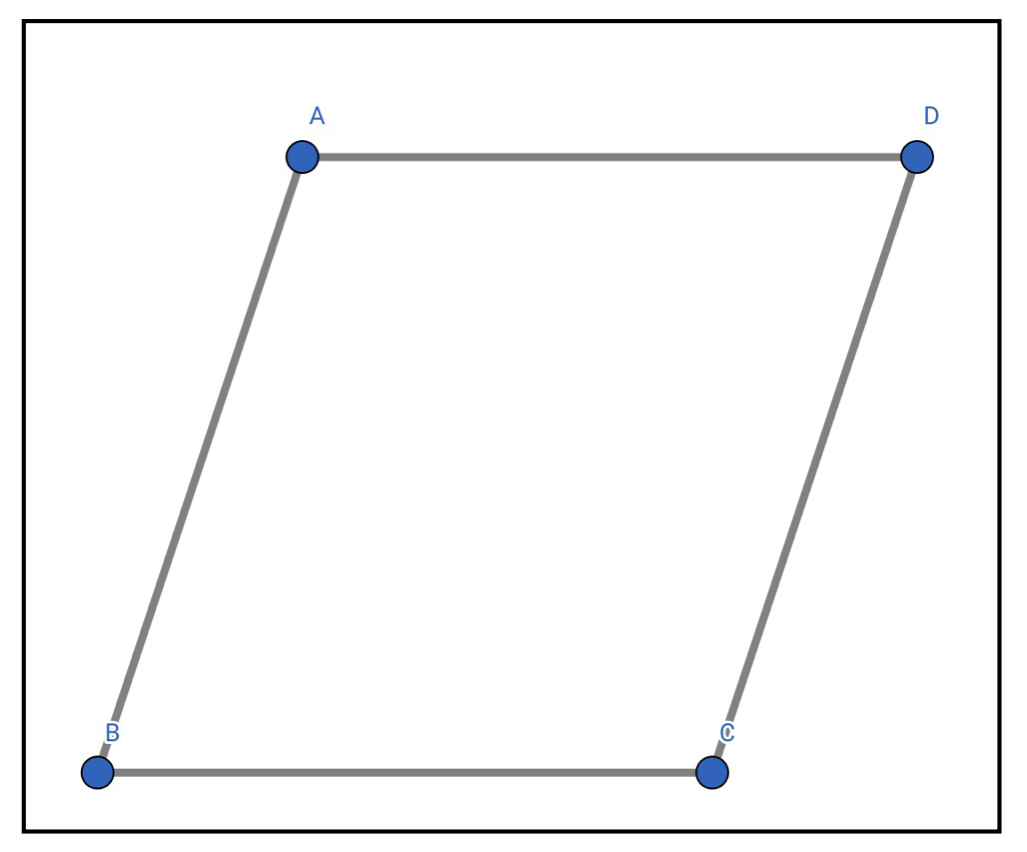
この図形の中から等しいベクトルを書き出せ。
向きと大きさの等しいベクトルを探せばいいので、以下のようになります。
\vec{AB}=\vec{DC},\quad\vec{BC}=\vec{DA}
\end{align}
例えば、このDCと書いているところをCDと書いてしまうと一つ目の等号は成立しなくなってしまうんです。なぜかというと、ベクトルの向きが右辺と左辺で反対向きになるからですね。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」
東大理系攻略法を
解説したPDF販売中！
中高一貫校に行かなくても、塾に行かなくても、独学で受かるための勉強法を完全解説！
全科目の参考書
全参考書の使い方
受験までの勉強スケジュール
が全てわかります！
今だけ！100様限定60%OFF！
さらに24時間以内なら返金保証つき！
無料サンプル公開！
