(※数式が見切れている場合は横スクロールしてください。)
この節は少し難しいかもしれませんが、頑張って理解してください。わからなければ2度3度読んでみてください。それでもわからなければ、コメントください。
質点mに外力を加えてゆっくり坂を登らせます。この時に2つのルートを考えることにしましょう。1つは最短距離で、もう1つは遠回りをします。以下の図を参考にしてください。
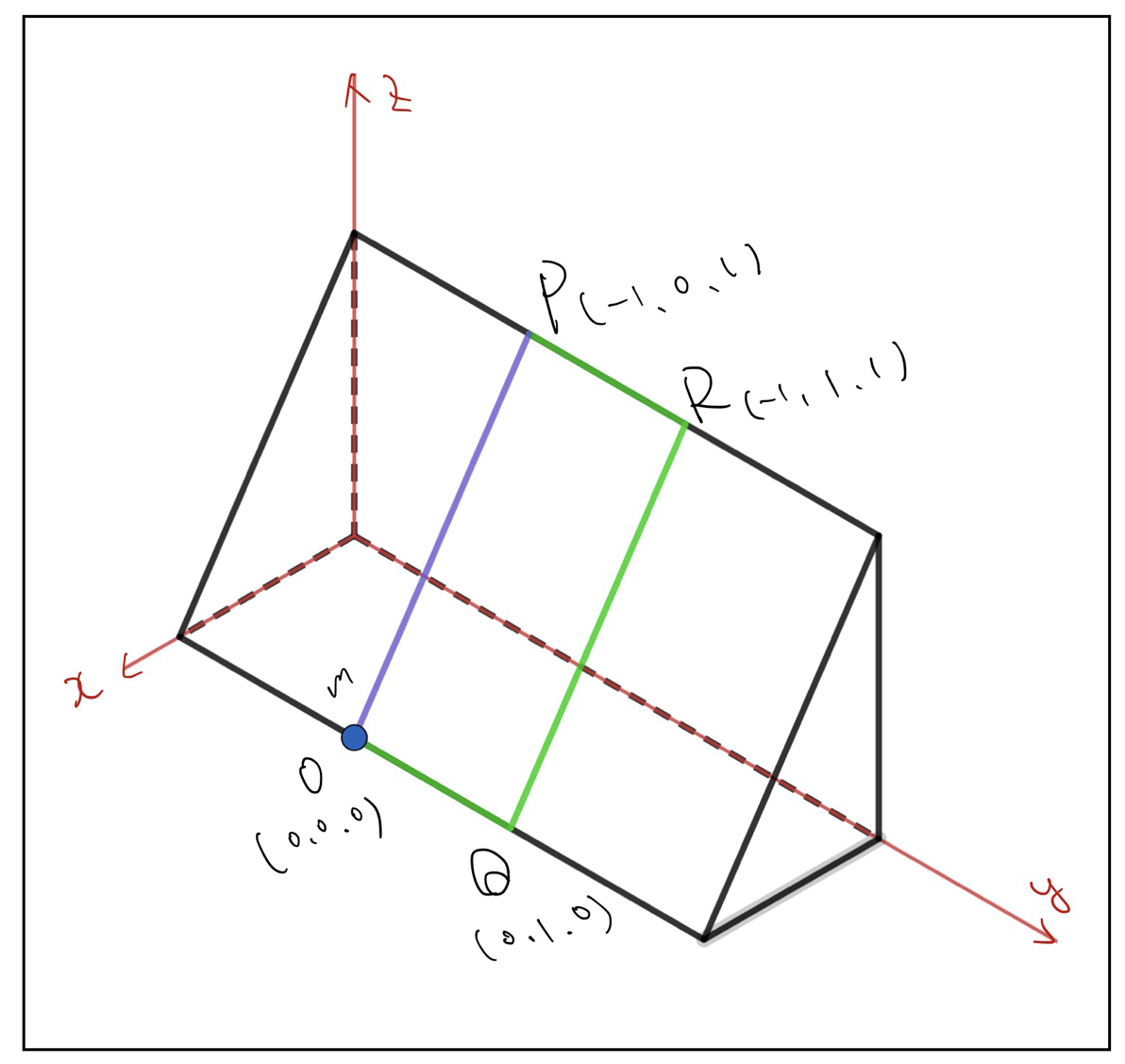
ルート1はO→Pのルート。ルート2はO→Q→R→Pのルートです。質点mに働く力は\(z\)軸方向の負の方向に働く重力と、坂道からの垂直抗力、そして坂道と質点mとの動摩擦力のみを考えます。
まずはルート1から考えます。OPを通る平面で三角柱を垂直に切断すると、以下の図のようになります。
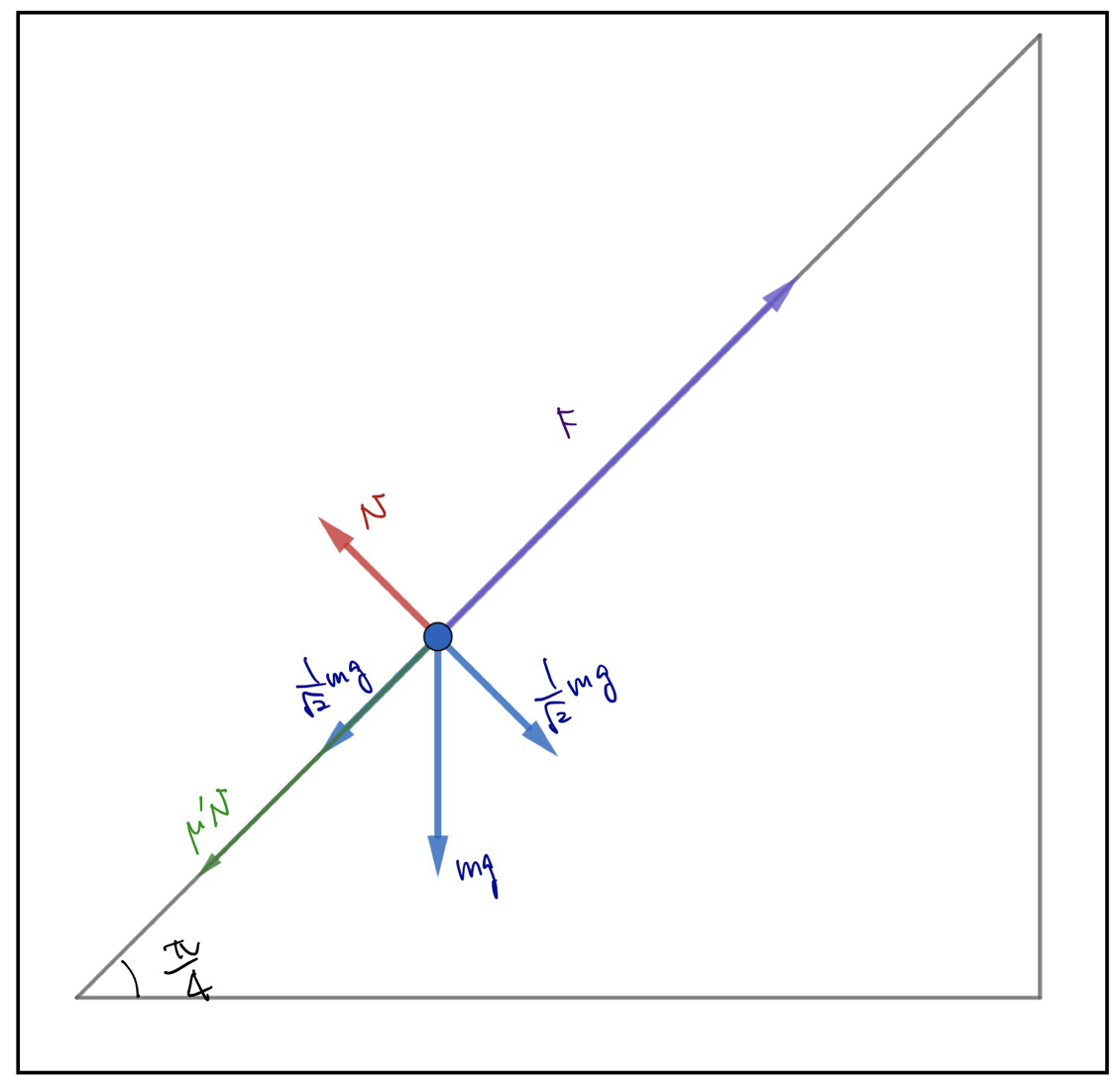
これくらいはそろそろ自力で描けるようになっていないとしんどいです。マキノさん、どうですか？描けました？ちなみに物理で「ゆっくり」と言われたら、各瞬間各瞬間で平衡状態（この場合はつりあいの状態）を保ちつつ、という意味ですので、そこから以下のような式が出てきます。
\begin{cases}
&N=\frac{1}{\sqrt{2}}mg\\
&F=\frac{1}{\sqrt{2}}mg+\frac{1}{\sqrt{2}}\mu’mg
\end{cases}
\end{align}
となります。ルート1を移動中は外力\(\vec{F}(t)\)は定数というわけですね。これに微小距離をかけて積分すれば、外力が質点に加えた仕事がわかります。
定数×微小距離の積分だと結局、微小距離の方だけに積分がかかって、定数に移動距離が掛け算された値が出るだけです。
OPの距離は\(\sqrt{2}\)ですので、最終的には、
\int^{t_P}_{t_O}\vec{F}(t)\cdot\vec{v}(t)dt=mg+\mu’mg
\end{align}
となりますね。点Oと点Pにいる時刻を\(t_O\)と\(t_P\)としました。ゆっくりという条件が入ると、実は速さという概念は消え失せてしまうのですが、それが今回は時間積分ではなく、空間積分でオッケーですよっていうことに繋がっています。この辺りは今後、余裕があれば解説するかもですが、だいぶ先の話になるはずです。
そして、最終結果は\(mg\)でくくることができるのですが、敢えて分けています。その意味はすぐあとに解説します。
次にルート2について考えてみます。ルート2のうち、Q→Rはルート1と全く同じなので、O→Qと、R→Pの部分について考えてみましょう。どちらも動く方向に働く力は動摩擦力だけで（向きは動く方向と逆）、先ほどと同じ大きさです。
定数に動いた距離をかけるだけなのは先ほどと同じで、O→Qで、外力は質点に
\frac{1}{\sqrt{2}}\mu’mg
\end{align}
の仕事を与えます。これが2回分と、ルート1と同じだけの仕事とを合わせて、ルート2では外力は以下の大きさの仕事をします。
mg+\mu’mg(1+\sqrt{2})
\end{align}
ここで、ルート1の結果とルート2の結果を比べてみましょう。どちらの場合にも、外力は重力に逆らう分の力と動摩擦力に逆らう分の力の合力を用いています。
重力に逆らう分の外力が質点にした仕事は、どちらのルートを選んでも\(mg\)となります。一方で、動摩擦力に逆らう分の外力がした仕事はルート1の方では\(\mu’mg\)、ルート2の方では\(\mu’mg(1+\sqrt{2})\)となりました。
この2つの性質を比べるために、各項を\(mg\)でくくらずにあえてそのままにしておきました。
ここまでの結果を以下の定義で保存力と非保存力という言葉を使っておさらいしておきましょう。
定義
重力のように、それに逆らう外力による準静的な（ゆっくりという意味）仕事が質点の通ってきた経路によらない力を保存力と言う。また、動摩擦力のように、それに逆らう外力による準静的な仕事が質点の通ってきた経路による力を非保存力と言う。
保存力に逆らう外力がした仕事は、スタート地点とゴール地点だけの情報で記述できます。それは通ってきた経路の情報は全く関係ないからですね。
このように経路によらない保存力に逆らって外力から加えられた仕事は、質点にエネルギーとして蓄えられます。スタート地点の位置と、ゴール地点の位置の情報で決まるので、位置エネルギーと読んだりするわけですね。
少し前の章で勉強してきたことともリンクさせていってくださいね。
外力は保存力に逆らって質点なり何なり仕事を与える形で、エネルギーを蓄えさせて、実はそのエネルギーは運動エネルギーに変換されうるポテンシャルを持っているので、ポテンシャルエネルギーと呼ぶこともあるという話を少し前にしています。
今回の例に戻ってこのあたりを見ておきましょう。
重力に逆らう外力がした仕事はルート1でもルート2でも\(mg\)でした。\(mg\)と見るとエネルギーの単位なのか、力の単位なのか混同してしまいそうなので、\(mg\cdot1\)と書くことにしますね。ちゃんと力×長さでエネルギーの単位になってます。
この\(mg\cdot1\)は点O（スタート地点もしくは基準点）から見たとき、点Pにいる質点mが持っている位置エネルギーと見ることができます。
なぜかというと、点Pで質点mから手を話すとコロコロと下に転がっていって、運動エネルギーに変わってくれますもんね。
さて、ここでいくつか問題を解きつつ、3次元での運動エネルギーやら位置エネルギーやらに少し慣れてもらうこととしましょう。
問題
以下の図のように質点mが摩擦はないが、よく見ると平坦でもない斜面の点Pに最初あったとする。その後、どのような経路を辿ったかは分からないが（平坦じゃないので、どんな道を選ぶかは分からない）、最終的に重力の影響を受けて、点Qまで下ってきた。
1.
重力がした仕事と、垂直抗力がした仕事を計算せよ。
2.
点Qの位置に下って来た時の質点mの速さを求めよ。
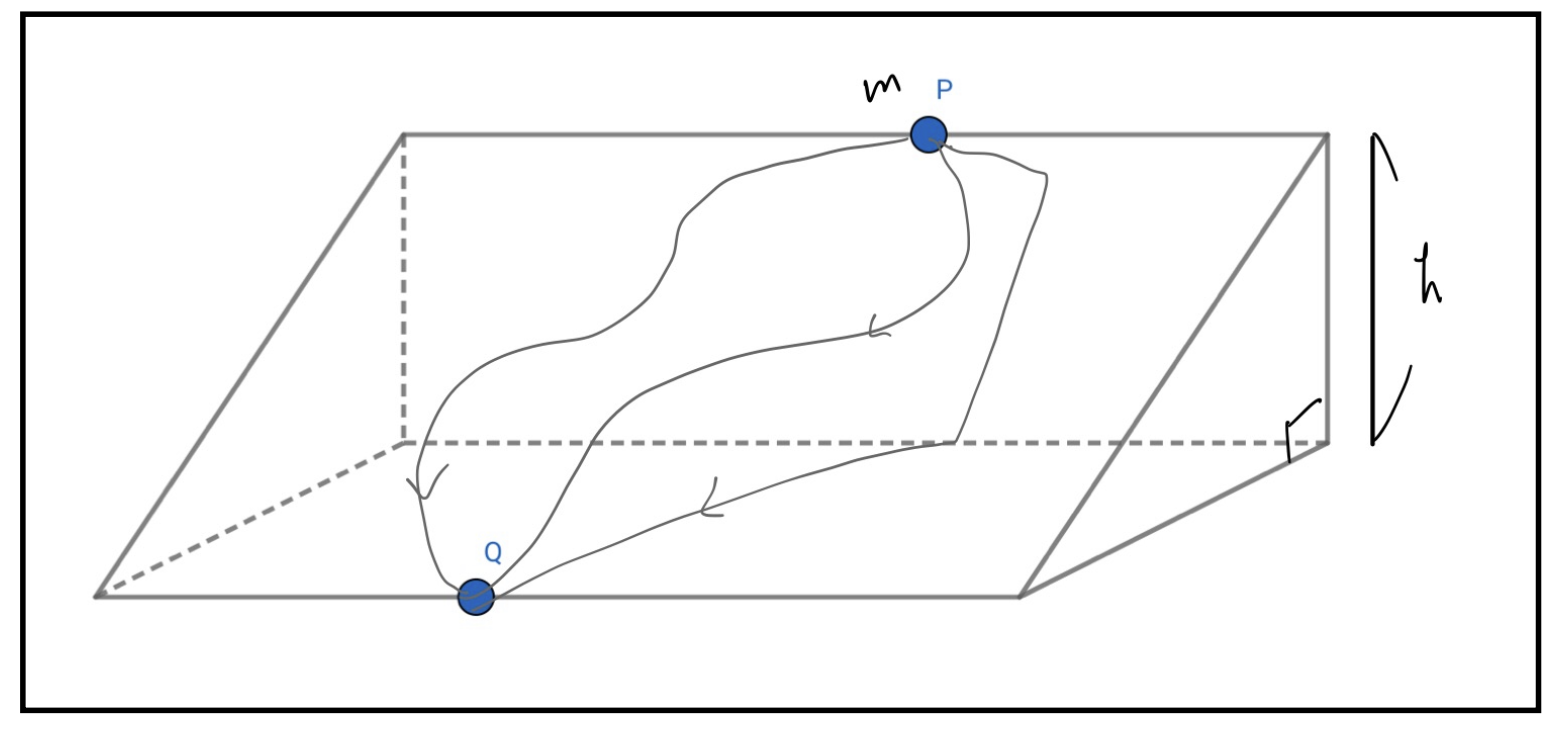
解答
1.
ちょっと面倒なのは坂道が平坦ではなかったり、斜面の角度が与えられていないということですかね。とは言え、実はよく考えるとそれほど難しくはありません。
重力の仕事は、「重力の大きさ」×「重力の方向への微小変位」の寄せ集めとも考えることができますね。
内積のcosをどちらにかかっていると見るかというのがポイントです。
そうしてみると、実は重力の大きさは一定ですし、重力の方向も一定です。だとすると、重力方向へいくら進んだかを計算するだけになってしまいますね。
結局、重力の方向にはだけ下ってきているので、重力のした仕事は\(mgh\)となります。
次に垂直抗力です。これもよく考えるとそれほど難しくありません。質点の微小変位はどの瞬間を取って来ても常に斜面の平面内です。一方で、垂直抗力はどうですか？
垂直抗力の向きは常に斜面と垂直です。
斜面に垂直な力と斜面に平行な微小変位の内積はどうなりますか？ゼロですね。内積の公式として覚えておくことをおすすめしたやつです。
というわけで、垂直抗力のした仕事はゼロです。
2.
さて、1番を計算できていれば、こちらは簡単で、運動エネルギーの変化は質点に加えられた仕事で記述できたわけですから、その公式に当てはめればいいです。
点Pと点Qでのそれぞれの質点の速度を\(\vec{v_P}\)と\(\vec{v_Q}\)とすると、
&\frac{m}{2}\left|\vec{v_Q}\right|^2-\frac{m}{2}\left|\vec{v_P}\right|^2=mgh\\
\Longleftrightarrow
&\left|\vec{v_Q}\right|=\sqrt{2gh}
\end{align}
となります。
この問題を少しだけ読み替えます。
点Pにいる時点で、誰かが外力を質点に加えて持ち上げたとすると、その時点で位置エネルギーを質点は持っています。
そして3次元でもやはり力学的エネルギーは保存すると思うと、そもそも以下のような式を書くこともできます。
\frac{m}{2}\left|\vec{v_P}\right|^2+mgh_P=\frac{m}{2}\left|\vec{v_Q}\right|^2+mgh_Q
\end{align}
\(h_P\)と\(h_Q\)は基準点をどこか適当に選んだ時、そこからの高さです。高さはもちろん重力とは逆向きの方向に取るのは大丈夫ですよね。
この式を使っても先ほどの解答と全く同じ答えが出てきます。どちらかというと、こちらの形を覚えておいて、力学的エネルギーの保存を使う方がわざわざ積分をしなくてもいいので、楽ではあります。
高校で習う場合には、最初からこの力学的エネルギーの保存の方から習うのがよくあるパターンなので、問題集なんかの解答には力学的エネルギーの保存則を使った形が書かれてある方が普通です。力学的エネルギーの保存を使う場合には、ばねの弾性エネルギーの形も覚えておくといいかなという感じですので、その問題を1つ扱ってそこまででこの節は終わりにします。
問題
図のように角度\(\theta\)のなめらかな斜面にばねを固定し、その先に質点mを付ける。（自然長の状態で手で支えておく。）
1.
ある瞬間に質点mにばねの縮む方向に速さを与えた。ばねがだけ縮んだとき、重力が質点にした仕事、ばねが質点にした仕事を求めよ。
2.
先ほどの問題の結果と運動エネルギーの変化を考慮して、力学的エネルギーの保存則を導け。
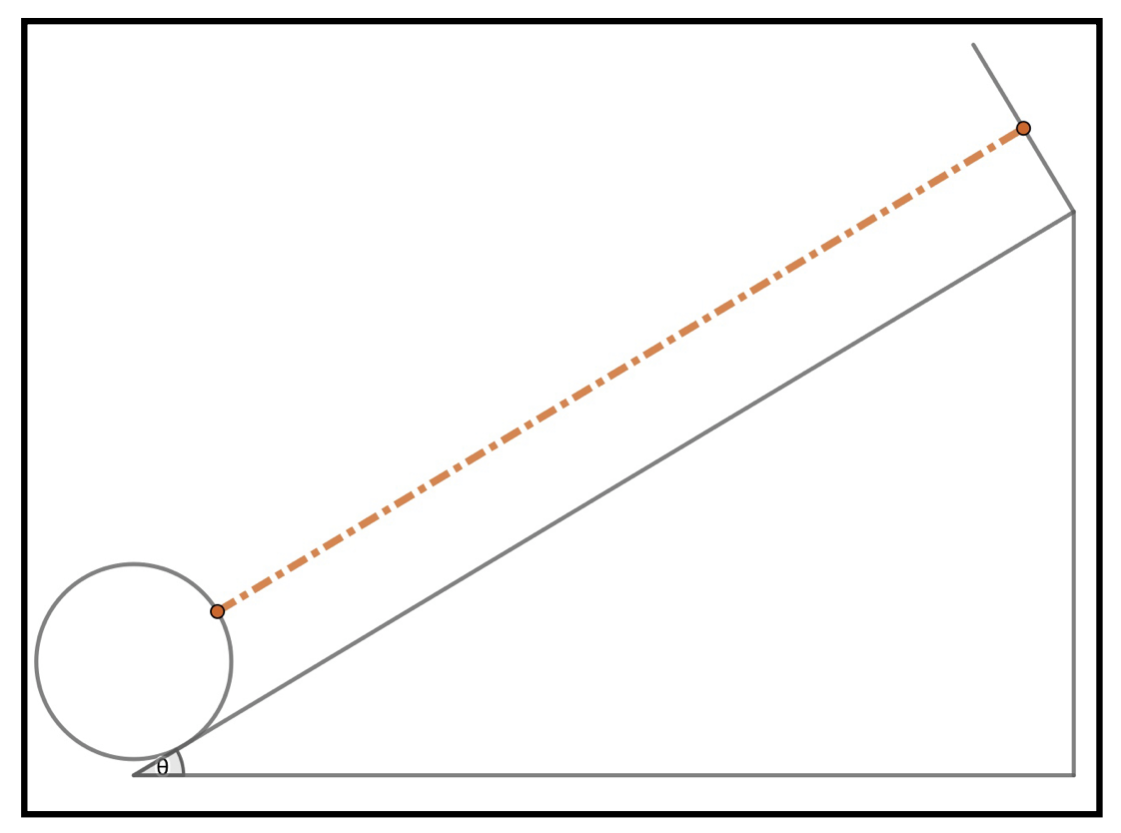
解答
1.
ばねの問題を扱う時には基本的にはばねの元々の長さ方向に伸び縮みする状況しか考えないので、1次元とほとんど考えることは同じです。
ばねが\(x’\)だけ縮んでいる時に質点にかかる斜面方向の力は、
F=-mg\sin\theta-kx’
\end{align}
となります。ここで斜面の上に向かう方向を正の方向としました。
これを空間積分すればいいわけですね。すでにここで書いた力はばねの伸び縮みする方向に取った力なので、内積などを考える必要はありません。
\(x’\)を\(0\)から\(x\)まで積分してやれば、\(F\)（重力と弾性力の合力）がした仕事が求まります。
\int^x_0(-mg\sin\theta-kx’)dx’=-mgx\sin\theta-\frac{1}{2}kx^2
\end{align}
この右辺の第1項が重力による仕事、第2項がばねの弾性力による仕事です。
2.
前問の仕事が運動エネルギーの変化なので、
\frac{m\left(v(x)\right)^2}{2}-\frac{mv_0^2}{2}=-mgx\sin\theta-\frac{kx^2}{2}
\end{align}
となります。ここから少し変形すると、以下のようになります。
&\frac{m\left(v(x)\right)^2}{2}+mgx\sin\theta+\frac{kx^2}{2}\\
=&\frac{mv_0^2}{2}+mg\cdot0+\frac{k\cdot0^2}{2}
\end{align}
この形にすると運動の前後で力学的エネルギーが保存していることが見えやすいですかね。
もう一度言いますが、運動量保存の式はベクトルを使った多成分の式だったのに対して、エネルギー保存の式はスカラーを使った1成分だけの式です。そこは意識するようにしておいてください。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」
東大理系攻略法を
解説したPDF販売中！
中高一貫校に行かなくても、塾に行かなくても、独学で受かるための勉強法を完全解説！
全科目の参考書
全参考書の使い方
受験までの勉強スケジュール
が全てわかります！
今だけ！100様限定60%OFF！
さらに24時間以内なら返金保証つき！
無料サンプル公開！
