(※数式が見切れている場合は横スクロールしてください。)
今度は少しスケールの大きな話をしていきます。惑星サイズのものがメインになってくるお話です。
万有引力の法則をまずは説明することにしましょう。万有引力という文字がいい説明になっています。質量を持つ万物（全てのもの）に有る（備わっている）引力です。
これだけだと意味不明ですかね笑
真面目に書いた以下の定義は覚えましょう。
定義
万有引力は質量を持つものが互いに互いを引き合う力である。質量\(M\)の物質が質量\(m\)の物質を引く力の大きさは、それらの物質間の距離\(r\)と万有引力定数\(G\)を用いて以下のように決まる。
\left|\vec{F}\right|=G\frac{Mm}{r^2}
\end{align}
物質Mから見た物質mの位置が\(\vec{x}\)と表すことができるとき、万有引力\(\vec{F}\)は以下のように書ける。
\vec{F}=-G\frac{Mm}{\left|\vec{x}\right|^2}\cdot\frac{\vec{x}}{\left|\vec{x}\right|}
\end{align}
\(GMm/\left|\vec{x}\right|^2\)の部分は先程書いた大きさを表している部分です。そして、\(-\vec{x}/\left|\vec{x}\right|\)の部分は向きを表す部分です。まず、\(\vec{x}/\left|\vec{x}\right|\)が単位ベクトルでかつ物質Mから見た物質mの向きを向いています。引力を表すためにはそこにマイナスをつけなければならないです。
図を見てイメージを正確に理解しておくといいですね。
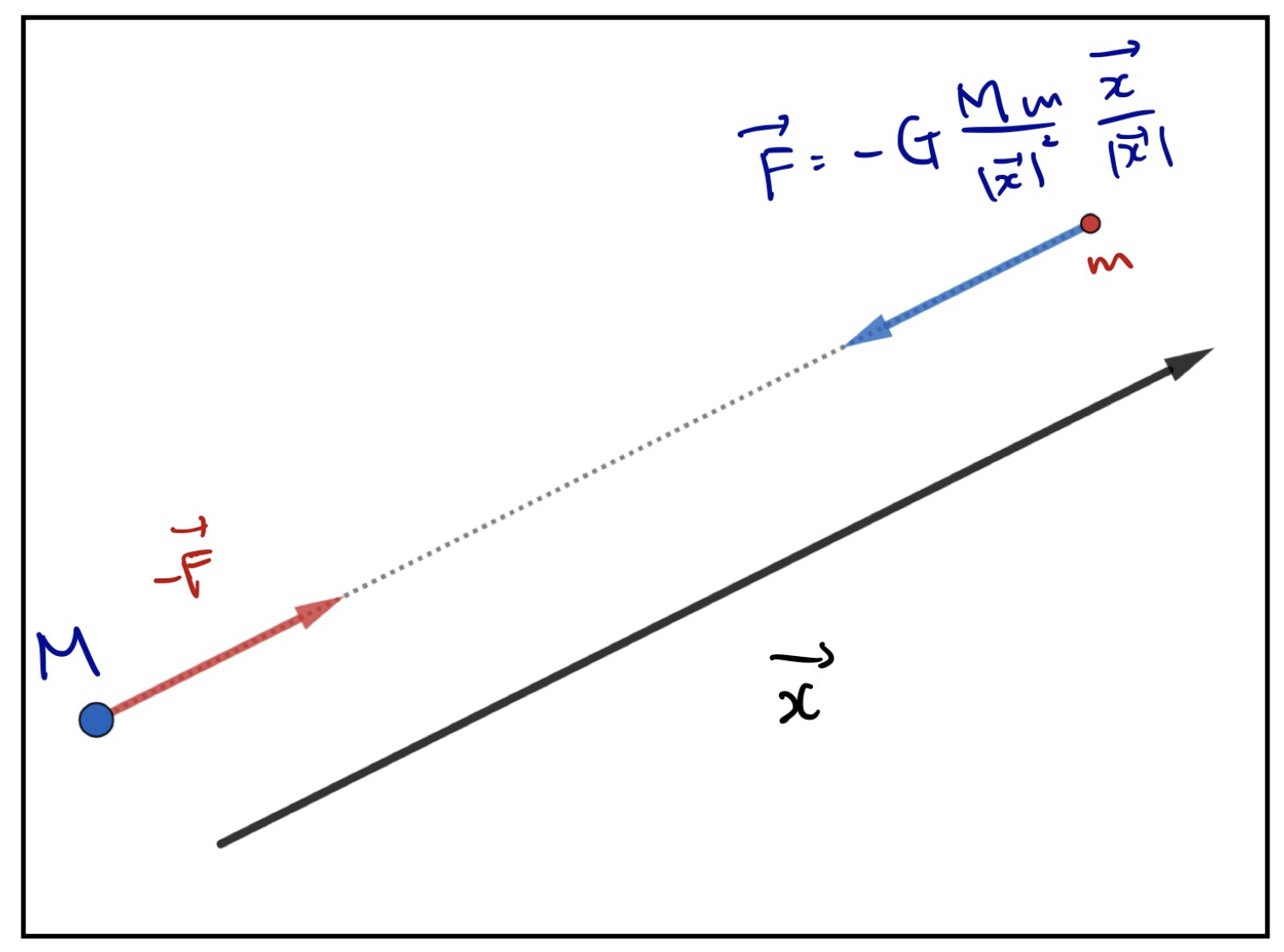
図には\(-\vec{F}\)が物質Mにかかっていることも明示しておきました。これは作用反作用の法則です。
壁とか床のように接触しているときにはイメージしやすいかもしれませんが、非接触の状態でも作用反作用の法則は成り立ちます。これは重要なポイントです。万有引力以外には静電気同士が引きあったり、反発しあったりする力も非接触ですが、これも作用反作用を忘れてはならないものの１つです。
次に、距離の2乗に反比例するという形も重要です。実は静電気同士に働く力も距離の2乗に反比例することが分かっています。逆2乗則と言います。万有引力と静電気力に共通するポイントがあることがわかりますね。
静電気力と万有引力は共通するポイントがあることがわかりますが、一方で違うところもあります。1つは「万有引力は常に引力なのに対して、静電気力は反発することもあるということ」です。2つ目は静電気力の方が身近に感じやすいということです。ふつうに生きていて、鉛筆同士が引き合う力を感じることはないですよね？
でも質量があるもの同士は常に引力が働いているんですから、鉛筆同士は引きあっていますよ。
もちろんマキノさんご自身だってそこら中のありとあらゆるものに引っ張られています。これを感じることは普段ありません。
万有引力と静電気力を比べると、万有引力は非常に小さいということになります。万有引力が大きくなるには、少なくとも\(M\)か\(m\)のどちらかはそれなりに大きい必要があるということです。ですからこの節の冒頭で説明したとおり、万有引力を扱うときには基本的には惑星などの星が主役になってくるわけです。
長くなりました。1つ問題を解いておきましょう。
問題
地球が止まっていると仮定して、重力加速度を\(g\)地球の質量\(M\)と半径\(R\)、そして万有引力定数を用いて表現せよ。
解答
地球の重力というのは、その成分のほとんどが地球が物体を引きつける万有引力でできています。正確には遠心力も考えなければならないのですが、今の段階ではそれは無視しておきましょう。
図を見てください。後々細かいことは扱いますが、地球の質量は地球の中心にあると思っておけば大丈夫です。地球の表面に質点mを置いてやって、その重力が万有引力と等しいと考えればいいです。
&mg=G\frac{mM}{R^2}\\
\Longleftrightarrow
&g=\frac{MG}{R^2}
\end{align}
と重力加速度を表現することができます。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」
東大理系攻略法を
解説したPDF販売中！
中高一貫校に行かなくても、塾に行かなくても、独学で受かるための勉強法を完全解説！
全科目の参考書
全参考書の使い方
受験までの勉強スケジュール
が全てわかります！
今だけ！100様限定60%OFF！
さらに24時間以内なら返金保証つき！
無料サンプル公開！
