(※数式が見切れている場合は横スクロールしてください。)
さて、この章の最後に惑星の運動についてより深いところへ一歩踏み込んでおきましょう。ここから先しばらく万有引力の法則に基づいてケプラーの法則を3つ理解していくことがメイントピックになります。
中学校の理科までで、地球は太陽の周りを公転していることはマキノさんもご存知でしょう。実は後で数学的に勉強する楕円軌道というものを地球は描いていることが分かっています。この軌道の話も含めてケプラーの法則は惑星と太陽の間の関係を説明しているものと思ってください。
第2法則はすぐにでも証明できるのですが、先に予告としてどんな内容を扱っていくかまとめておきましょう。
ケプラーの法則
- 惑星は太陽を焦点の1つとする楕円軌道を周回する。
- 惑星と太陽を結ぶ線分が単位時間あたりに掃く面積は一定である。（面積速度一定）
- 楕円軌道の長半径\(a\)と公転周期\(T\)には以下の関係式が成り立つ。
\frac{T^2}{a^3}=C
\end{align}
ここで\(C\)は定数で全惑星に共通の値です。
この節ではまず第2法則だけ考えていきましょう。第2法則はまず日本語の意味を理解することが大事です。以下の図を見てください。
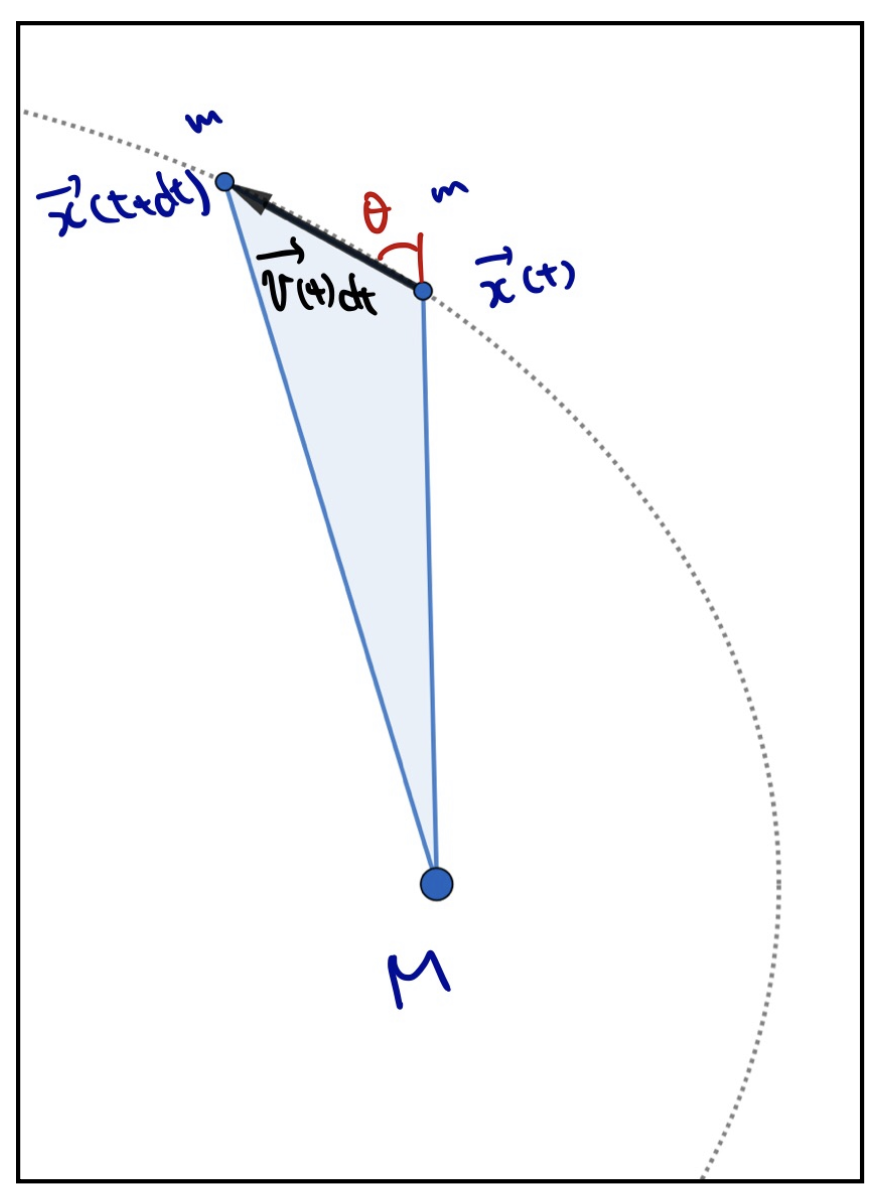
太陽が質点M、地球が質点mだと思ってください。このとき質点mが図のように楕円運動をします。質点Mから見た質点mの位置を\(\vec{x}(t)\)とすると、時刻\(t\)から時刻\(t+dt\)の間に\(\vec{x}\)は図の青く塗った部分を通っていきますね。ポイントは\(\vec{x}\)というベクトル全体が通っていく場所ということです。
この面積をそこを塗るのにかかった時間\(dt\)で割ったものが面積速度というものです。何となくお分かりいただけたでしょうか。では実際にこの面積速度が一定であることを示しましょう。
先ほどの図のように微小時間\(dt\)の間であれば、実際に\(\vec{x}(t)\)が掃いた面積は三角形で近似できます。底辺の長さが\(\left|\vec{x}(t)\right|\)で、高さが\(\left|\vec{v}(t)\right|dt\sin\theta\)なので、その面積は
\frac{1}{2}\left|\vec{x}(t)\right|\cdot\left|\vec{v}(t)\right|dt\sin\theta
\end{align}
となります。これを\(dt\)で割ったものが面積速度ですから、以下のように表現できますね。
\frac{dS}{dt}=&\frac{1}{2}\left|\vec{x}(t)\right|\cdot\left|\vec{v}(t)\right|\sin\theta\\
=&\frac{1}{2}\left|\vec{x}(t)\times\vec{v}(t)\right|=\frac{\left|\vec{L}(t)\right|}{2m}
\end{align}
ここで、面積速度の時間依存は質点mの質点M周りの角運動量が一手に引き受けてくれることがわかりました。
今、質点mが受けている力は万有引力だけのとき、万有引力は中心力なので、角運動量は保存します。つまり時間に依存しないってことですね。ってことは、もちろん面積速度も時間によらず一定ということです。
ポイントは面積速度の時間依存を角運動量が引き受けてくれることと、万有引力が中心力であるということですね。このケプラーの第2法則を使って次の問題を解いてみましょう。
問題
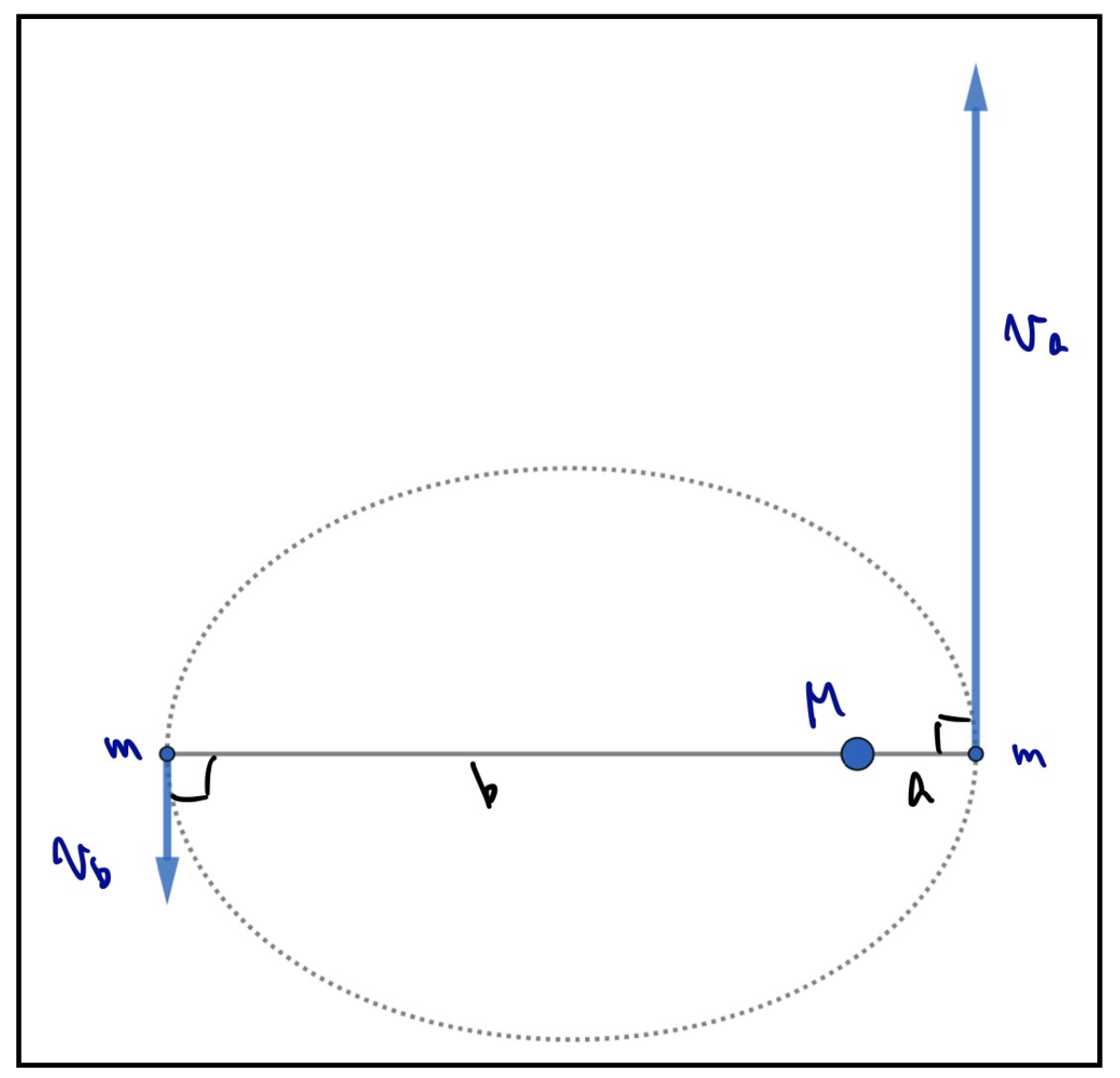
質点mが、固定された質点Mを焦点とする楕円運動をしている。
このとき、図のように質点Mに1番近いところに質点mがあるときと、1番遠いところに質点mがあるときの速さの比を求めよ。
ただし、その瞬間の距離は図のように\(a\)と\(b\)とする。
解答
面積速度は角運動量に比例していますから、角運動量をそれぞれの瞬間で計算すればいいです。
&\frac{av_a}{2m}=\frac{bv_b}{2m}\\
\Longleftrightarrow
&\frac{v_a}{v_b}=\frac{b}{a}
\end{align}
あとで、楕円についても詳しく説明しますが太陽に近い位置を動いている時の方が、太陽から遠い位置を動いている時より地球の公転のスピードは速いということですね。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」
東大理系攻略法を
解説したPDF販売中！
中高一貫校に行かなくても、塾に行かなくても、独学で受かるための勉強法を完全解説！
全科目の参考書
全参考書の使い方
受験までの勉強スケジュール
が全てわかります！
今だけ！100様限定60%OFF！
さらに24時間以内なら返金保証つき！
無料サンプル公開！
