(※数式が見切れている場合は横スクロールしてください。)
ケプラーの法則の話に戻っていきましょう。
次のような状況を考えます。
例
原点に質量\(M\)の質点Mを固定する。
その質点Mから万有引力のみを受けている質量\(m\)の質点ｍの運動の軌道を考える。
ただし、万有引力\(G\)とし、質点ｍの運動は\(z\)平面上とする。
質点mの運動方程式は以下のようになります。
ma_r=m(\ddot{r}-r\dot{\theta}^2)=-\frac{mMG}{r^2}\\
ma_\theta=m\frac{1}{r}\frac{d}{dt}(r^2\dot{\theta})=0
\end{cases}\end{align}
角度方向の運動方程式から、\(r^2\dot{\theta}\)は保存します。
r^2\dot{\theta}=2L
\end{align}
と置けます。もちろん\(L\)は定数です。さらに\(u=1/r\)とおくと、
\dot{\theta}=2Lu^2
\end{align}
となります。これらのわざわざ置きなおした文字を使って\(r\)方向の運動方程式を計算するために\(r\)を微分したものを準備しておきます。
\dot{r}=&\frac{d}{dt}\frac{1}{u}\\
=&-\frac{1}{u^2}\dot{u}\\
=&-\frac{2L}{\dot{\theta}}\frac{du}{d\theta}\dot{\theta}\\
=&-2L\frac{du}{d\theta}
\end{align}
途中で\(du/dt=du/d\theta\cdot d\theta/dt\)を使いました。
\ddot{r}=&-2L\frac{d^2u}{d\theta^2}\dot{\theta}\\
=&-4L^2u^2\frac{d^2u}{d\theta^2}
\end{align}
これらを\(r\)方向の運動方程式に代入します。
&-4L^2u^2\frac{d^2u}{d\theta^2}-\frac{1}{u}\cdot 4L^2u^4=-MGu^2\\
\Longleftrightarrow
&\frac{d^2u}{d\theta^2}+u=\frac{MG}{4L^2}
\end{align}
少し移項して書きなおすと、単振動の方程式と同じ形になります。
\frac{d^2}{d\theta^2}\left(u-\frac{MG}{4L^2}\right)=-\left(u-\frac{MG}{4L^2}\right)
\end{align}
これは以下のように解くことができます。
u-\frac{MG}{4L^2}=A\cos\theta+B\sin\theta
\end{align}
初期条件はまだ与えていなかったので、\(B=0\)とします。
このとき、以下のように\(u=1/r\)として計算を進めると2次曲線の形になります。
&\frac{1}{r}-\frac{MG}{4L^2}=A\cos\theta\\
&r=\frac{\frac{4L^2}{MG}}{\frac{4L^2}{MG}A\cos\theta+1}
\end{align}
準線\(x=a\)で、離心率\(e\)の2次曲線の式は
r=\frac{ea}{1+e\cos\theta}
\end{align}
なので、比較すると
e=\frac{4L^2A}{MG},\quad a=\frac{1}{A}
\end{align}
という対応になっていることがわかります。実際に図示してみるとこんな感じです。
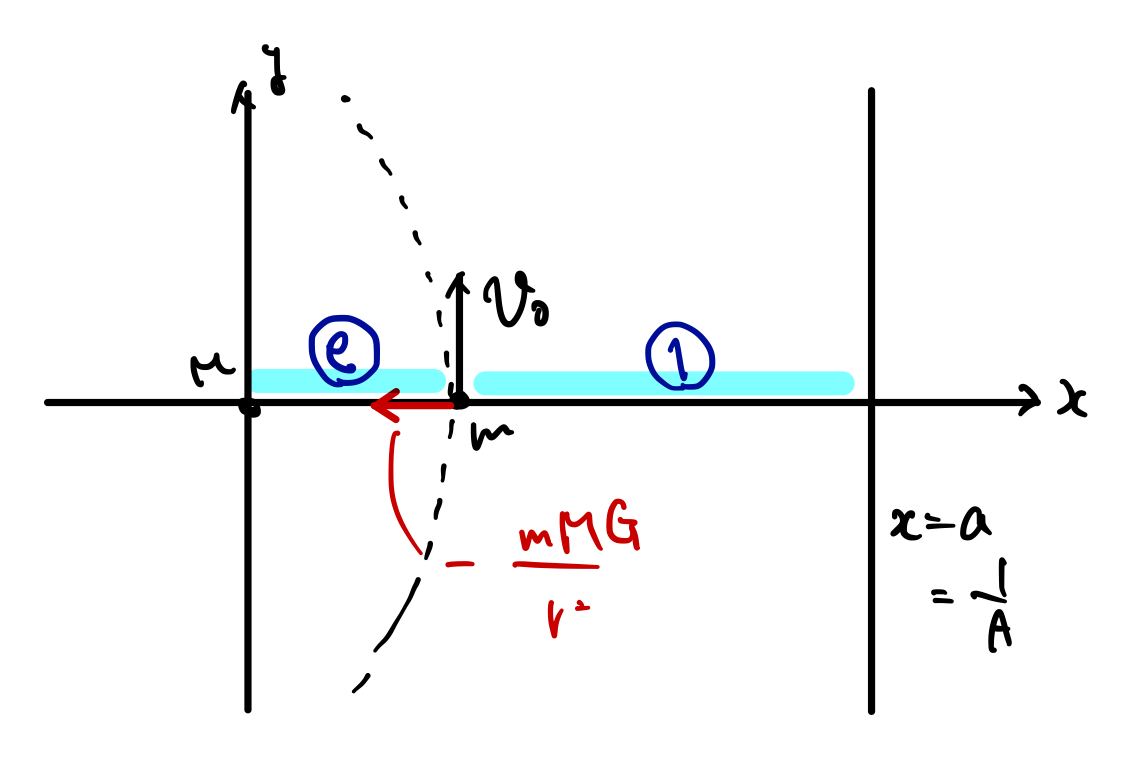
ここまでの計算で、万有引力だけの力で運動するときには2次曲線の軌道を描くことが分かります。
その軌道がだ円になるのか、放物線になるのか、双曲線になるのか、というのは\(e\)と\(1\)の大小を比較して決まります。
この\(e\)と\(1\)の大小は力学的エネルギーと関連があることを以下で見ていきます。\(L\)は定数なので、初期条件だけで求めたものがずっと続きます。
\(\theta=0\)のとき、\(r=x_0\)で始線に対して直角に\(v_0\)の初期条件とします。
4L^2=&(2L)^2\\
=&r^2\cdot (r\theta)^2\\
=&x_0^2v_0^2
\end{align}
という感じです。\(v_0^2=4L^2/x_0^2\)がわかりますので、これを使って力学的エネルギーを計算していきます。
E=&\frac{1}{2}mv_0^2-\frac{mMG}{x_0}\\
=&\frac{1}{2}m\frac{4L^2}{x_0^2}-\frac{mMG}{x_0}\\
=&\frac{m}{2x_0}\left(\frac{4L^2}{x_0}-2MG\right)\\
\end{align}
ここで、2次曲線の\(e\)と準線の関係から、\(x_0\)と\(A\)がどのような関係になっているかわかります。
x_0=\frac{e}{e+1}a=\frac{4L^2}{(e+1)MG}
\end{align}
それを力学的エネルギーに代入すると
E=&\frac{m}{2x_0}\left(4L^2\frac{(e+1)MG}{4L^2}-2MG\right)\\
=&\frac{mMG}{2x_0}(e-1)
\end{align}
ここまで進めると、\(e-1\)の正負と\(E\)の正負が一致することがわかります。
\(0<e<1\)のときに、だ円だったので、\(E\)が負ならだ円となります。
同様に\(e=1\)のとき、すなわち\(E=0\)のとき、放物線。
\(e>1\)のとき、すなわち\(E>0\)のとき、双曲線となることがわかります。
\(E<0\)というのはここまで見慣れていないと思いますが、よくある話です。後ほど少々解説することにします。
だ円上を動く形になるのはケプラーの法則の1つでしたので、ケプラーの法則で残るところは1つとなります。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」
東大理系攻略法を
解説したPDF販売中！
中高一貫校に行かなくても、塾に行かなくても、独学で受かるための勉強法を完全解説！
全科目の参考書
全参考書の使い方
受験までの勉強スケジュール
が全てわかります！
今だけ！100様限定60%OFF！
さらに24時間以内なら返金保証つき！
無料サンプル公開！
