(※数式が見切れている場合は横スクロールしてください。)
高校数学に入って早々に微分に入っていきますよ。ちょっと面倒に感じる部分はあるかもしれませんけど、ゆっくり読んで理解していってください。次のグラフに注目してください。
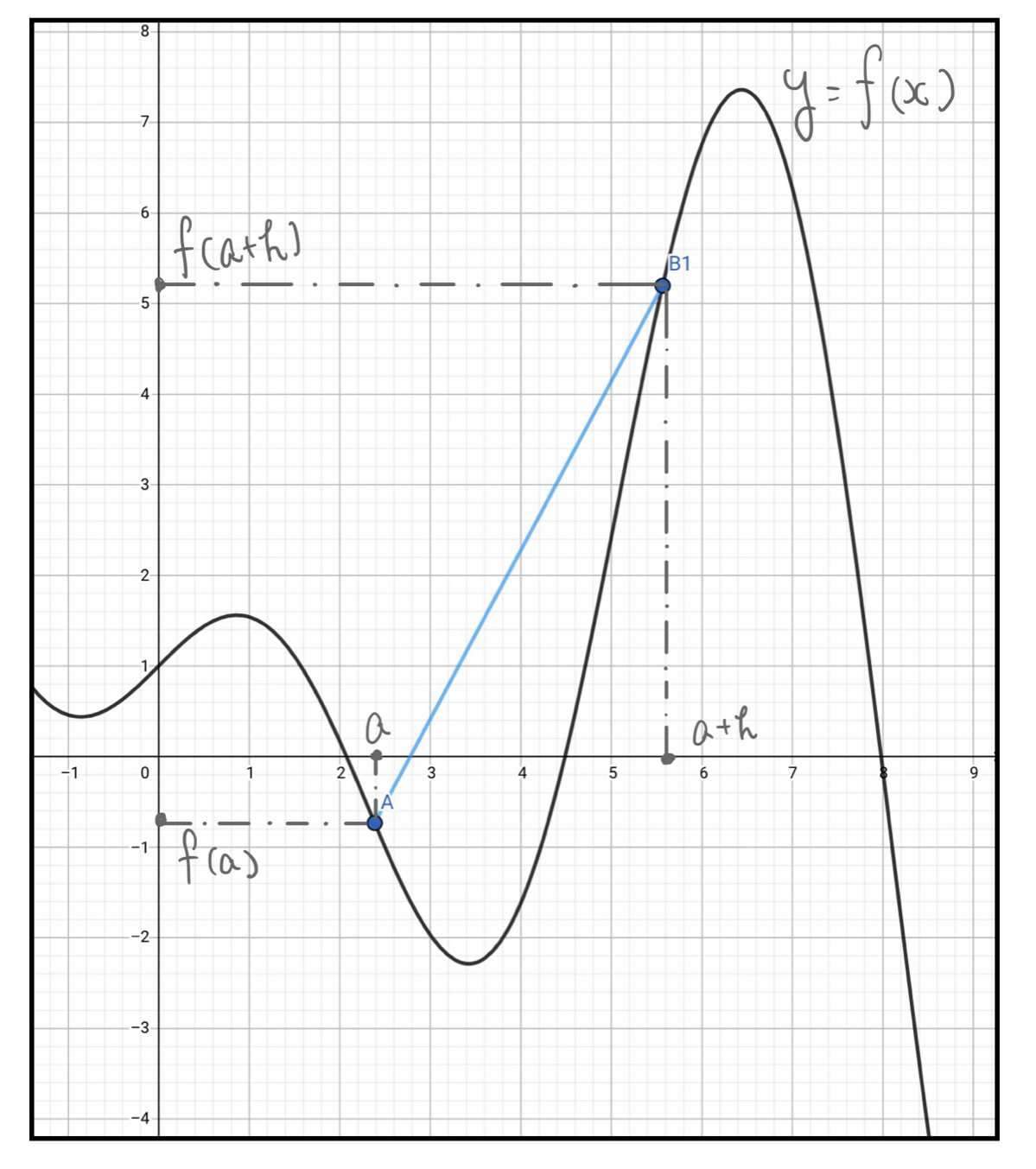
このグラフの点Aと点B1を結ぶ直線の傾きは、
\frac{f(a+h)-f(a)}{(a+h)-a}=\frac{f(a+h)-f(a)}{a}
\end{align}
となりますね。（ここまでは中学範囲ですよ！）
点B1を徐々に点Aに近づけていく（\(h\)をゼロに近づけていく）と以下の図のようになっていきます。
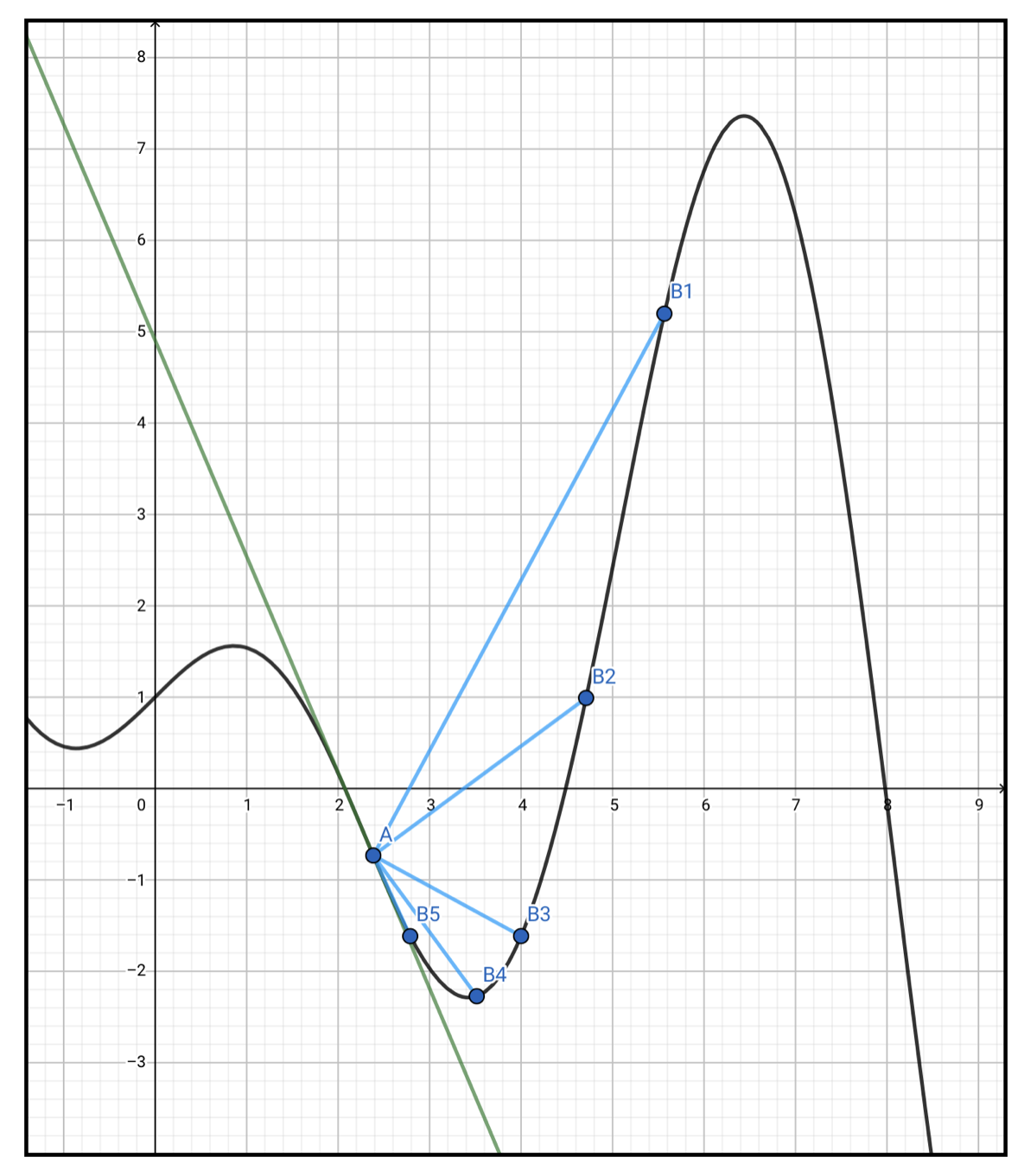
点Bが少しずつ点Aに近づくとそれを結ぶ直線は\(y=f(x)\)の接線に近づいていきます。そして完全に点Bが点Aに重なる極限では、先程の傾きは \(y=f(x)\) の点Aでの傾きとなります。これが微分の本質です。
定義
\frac{d}{dx}f(x)|_{x=a}=\lim_{h\to a}\frac{f(a+h)-f(a)}{h}
\end{align}
この左辺を \(f(x)\) の \(x=a\) での微分係数という。
この微分係数を \(f’(a)\)とプライム付きで表示することがあるのでそれも知っておいてください。（\(d/dx\)の部分が微分記号と思ってくれたらオッケーです。）
ここまでで、\(y=f(x)\)上の一つの点Aを決めたときにその接線の傾きを極限計算で求められることがわかりました。でもわざわざ点Aと決めなくても \(y=f(x)\) 上の任意の点における接線の傾きを知りたいってこともあります。
その場合には、先程の点Aを動かして、\(f’\)がどのような関数になるかを考えれば良いわけです。（ちょっと難しいかもしれないですけど、問題を解いてるうちに慣れます。）その関数のことを導関数と言います。
定義
f'(x)=\frac{d}{dx}f(x)=\lim_{h\to0}\frac{f(x+h)-f(x)}{h}
\end{align}
問題
導関数 \(f’(x)\)と微分係数 \(f’(2)\) を求めよ。
&1.\quad f(x)=3x+5\\
&2.\quad f(x)=x^3+x
\end{align}
解答
1.
f'(x)=&\lim_{h\to0}\frac{3(x+h)-5-3x+5}{h}\\
=&\lim_{h\to0}3=3\\
f'(2)=&3
\end{align}
2.
f'(x)=&\lim_{h\to0}\frac{(x+h)^3+(x+h)-x^3-x}{h}\\
=&\lim_{h\to0}(3x^2+3xh+h^2+1)\\
=&3x^2+1\\
f'(2)=&3\cdot2^2+1=13
\end{align}
これでマキノさんも微分ができるようになってしまいました。明日から自慢できますね。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」
東大理系攻略法を
解説したPDF販売中！
中高一貫校に行かなくても、塾に行かなくても、独学で受かるための勉強法を完全解説！
全科目の参考書
全参考書の使い方
受験までの勉強スケジュール
が全てわかります！
今だけ！100様限定60%OFF！
さらに24時間以内なら返金保証つき！
無料サンプル公開！
