(※数式が見切れている場合は横スクロールしてください。)
ではでは力の種類をザッと勉強していきましょう。
重力
質量のある物体に対して、地球の中心に向かうようにかかる力と覚えてください。（宇宙だとどうなんの？みたいな話は後で出てきます。）
質量mの物体には重力加速度gを質量にかけたmgの大きさの重力がかかります。
本当は地球上でも「重力は万有引力と遠心力の合力」なんですけど、それもまだまだ先の話ってことで今のところは勘弁しておいてください。
垂直抗力
物体同士が接触しているときに、接触面に対して垂直に働く力のことです。重力のように垂直抗力の大きさはこうなります！みたいなことは言えません。
ほとんどの問題では、他の情報から、垂直抗力の大きさを決める形になります。
ばねによる弾性力
ばねとつながった物体に働く力のことです。ばねが自然長（ばねのもとの長さ）から伸びたときには、ばねを縮める方向に、自然長から縮んだ場合にはばねが伸びる方向に働きます。
力がどちら向きに働くかはイメージ通りですよね？
ばねの伸びを\vec{x}で表現すると、（伸びの大きさをベクトルの大きさxで、伸びもしくは縮みをその向きで表現）、ばねによる弾性力の向きはと逆向きになります。
このばねの伸び（もしくは縮み）の大きさに対して弾性力の大きさは比例し、比例定数kをばね定数（正の定数）と呼びます。ですから、ばねによる弾性力はベクトルで表現すると、
です。（ちゃんと\vec{x}と逆向きになってますよね。）
ちなみに、ばねkという表現を使うときには、ばね定数kのばねを使っていると考えてください。一々ばね定数がkのばねって表現するよりは楽なので。
ばね定数が大きいときには、そのばねの持っている能力が高く（ばねが強い）弾性力の大きさは大きくなります。
以下の図を見てイメージを固めてください。
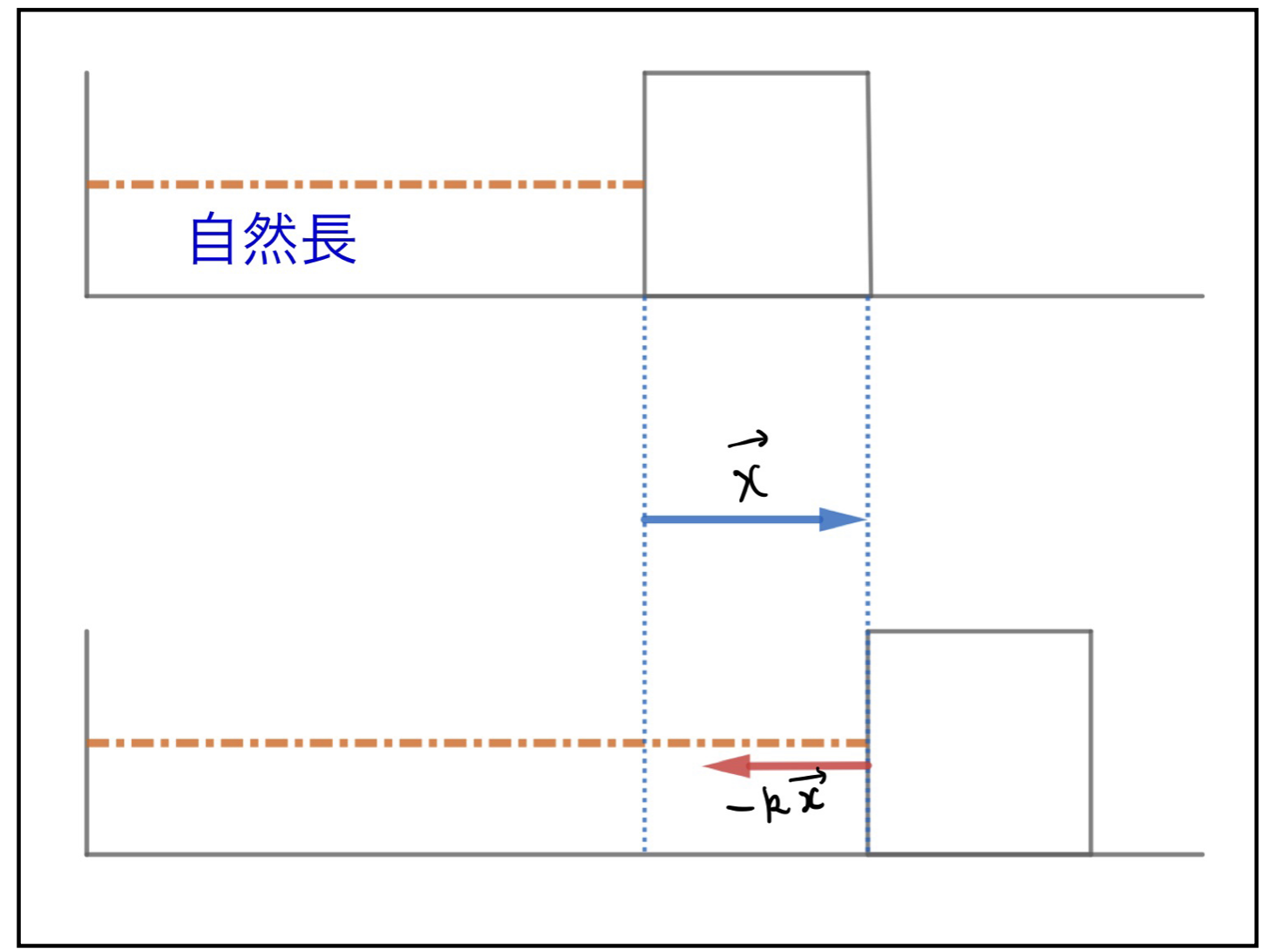
ちなみにばねをこのように表現したんですけど、今後もっとうまく描く方法が分かったら図を差し替えます。。。
張力
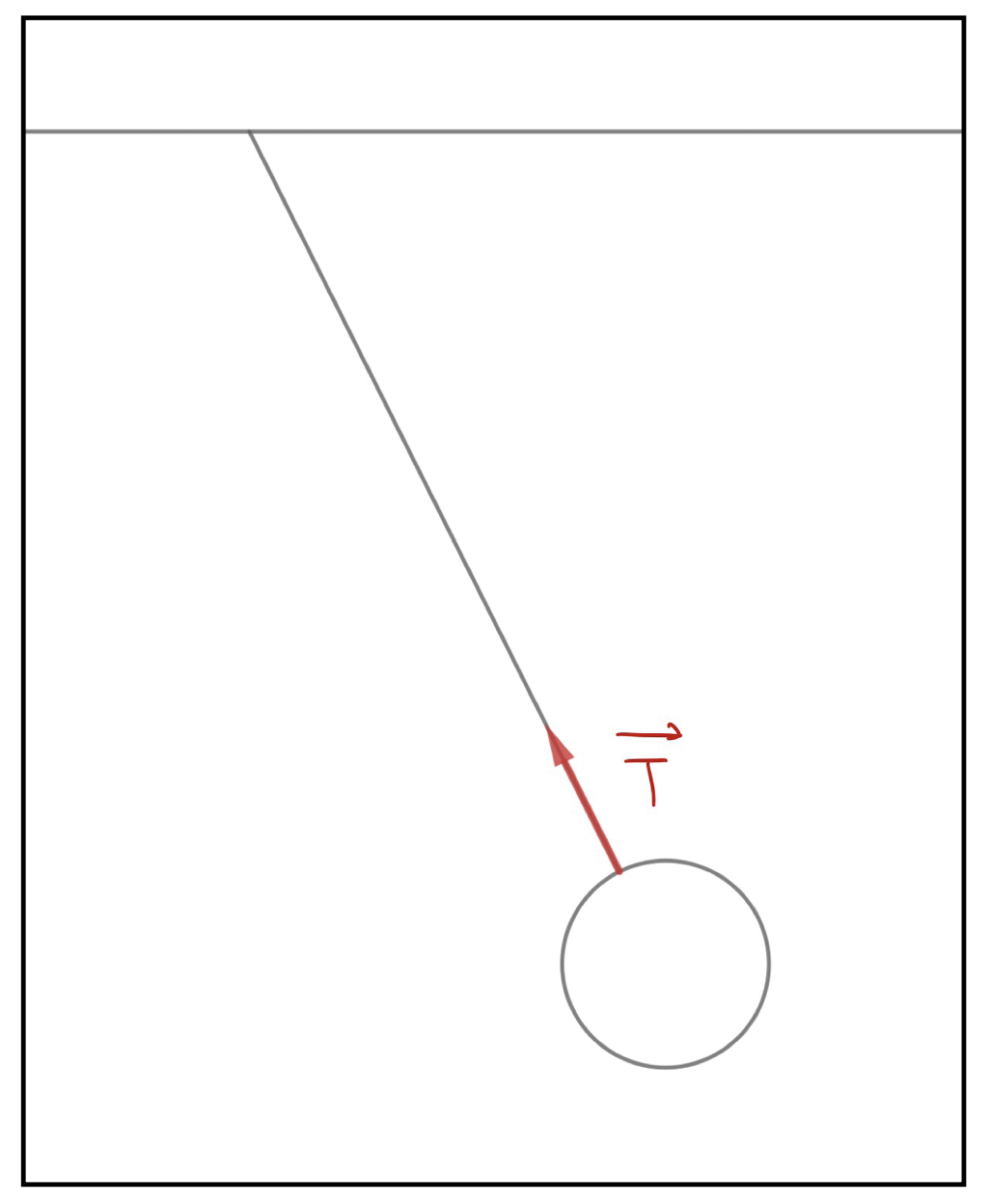
伸び縮みを考慮しない糸や棒などにつながれた物体が、そのつながれた糸や棒などに引かれる力のことを張力と言います。
糸や棒の繋がっている方向へ向かって働きます。
張力の大きさは人為的に決められている場合を除くと、垂直抗力と同様で、他の条件などから決まることがほとんどです。なので張力の大きさは考えている問題の設定によると思っておいてください。
特に大事なポイントの1つとして、質量の無視できる糸の両端からは同じ大きさで逆向きの張力が発生するということも覚えておいてください。
浮力
液体や気体などの流体中にある固体にかかる力と思っておいてください。正確には形が決まっていればそれで十分なので容器に入った流体を別の流体の中に入れると浮力は生じます。
浮力は重力とは逆向きにかかります。
浮力の大きさは外側の流体の密度の\rho（ギリシャ文字のロー）、重力加速度のg、そして固体の存在により、本来その場にあるはずだった流体の体積Vの積で与えられます。
ちょっとイメージ掴みにくいかもしれないので、図を見て納得してください。
重力とは逆向きにかかる力なので、負符号をつけて、浮力は以下のようなベクトルで表記できます。
静止摩擦力
床などに静止している物体を、動かそうとしたときに、その動かそうとする力に反するようにかかる力を静止摩擦力と言います。
ちなみに動き出した後は動摩擦力として扱う必要があるので、動き出す前まで静止摩擦力と表現することを覚えておいてください。
静止摩擦力の大きさは、加える力によって大きさが変わります。例えば、停車中のトラックを子供一人や、成人一人の力で動かすことは難しいですね。それは静止摩擦力によるものですけど、子供の力に対抗する静止摩擦力と成人の力に対抗する静止摩擦力では大きさが異なるわけです。
日本人らしくオノマトペを使って説明してみますね。
ある物体が床に静止してます。その物体は「チョンと」押しても「グッと」押しても動きませんでした。静止摩擦力は「チョンと」押された時には「チョン」に対応するだけの大きさになり、「グッと」押されたときには「グッ」に対応するだけの大きさになるということです。伝わりますかねえ？
でもでも、ですね。その押す力がめちゃめちゃ強かったときには動き出すわけですよね。要するに、いつまでも静止摩擦力が強くなるってことはないわけです。最大値というのが決まっていて、それを最大静止摩擦力と呼びます。
徐々に物を動かす力を大きくしていくと、それに対応するように徐々に静止摩擦力は大きくなるわけですけど、最大静止摩擦力を超えたその瞬間に物は動き始めるというわけです。
静止摩擦力の向きはもちろん、物体を動かす力に反する方向です。言い換えて、物体が静止するために必要な力の方向です。さらに言い換えると物体にかかる合力がゼロになるために必要な力の方向です。
最大静止摩擦力は、物体が接触している相手との相性、そしてそこから受ける垂直抗力の大きさによって決まります。
垂直抗力の大きさNと、静止摩擦係数\mu（ギリシャ文字のミュー）の積が最大静止摩擦力となるわけです。
ここまでをまとめると静止摩擦力の大きさfは以下の式を満たします。
\muは摩擦を起こす2面の性質と相性によって決まり、道路のアスファルトと、車のタイヤゴムなどは\muが大きくなるように作られていますし、逆に凍った道で車がスリップしやすいのはこのときに\muが小さくなっているからです。
動摩擦力
動摩擦力は動いている物体が、接触している面から受ける力で、動きを阻害する向きに働きます。
静止摩擦力の時とは違って、動摩擦力は基本的には一定の値を常にキープします。以下のような大きさです。
動摩擦係数\mu’と垂直抗力Nの積が動摩擦力の大きさとなっていますね。
先程と同じで、動摩擦係数は接触面同士が滑りやすいか滑りにくいかなどの相性の問題で決まります。
以下の図のような形になりますね。
それぞれの力に慣れておくために問題をいくつか解いておきましょう。
問題
質量mの箱が床に静止している。その箱に水平方向にFの力を加える。このFをだんだんと大きくしていくとあるところで、箱が横に滑り始めた。そのときのFの大きさは？
箱の回転は考えないこととする。静止摩擦係数は\muとする。
解答
滑り始めるその瞬間の摩擦は最大静止摩擦力です。以下のように図を書いて、ベクトルの大きさを比較することで、問題を解くことができます。まずは図をちゃんと描けるようになるのが一番大事です。
床面に対して垂直方向に力がつりあっているので、
また、滑り始めた瞬間まで、Fと静止摩擦力はつりあっているので、
最後の等号で、垂直抗力と重力がつりあっていることを使いました。
問題
水槽に密度\rhoの水を入れ、その水の中に体積V密度\rho’の箱を全て浸かるように入れた。水に入れた箱の底にばねkの一端を取り付け、逆の端は水槽の底に固定した。
十分な時間放置すると、ばねがx伸びたところで箱は静止をした。このときのばねの伸びxを求めよ。
解答
箱が水から受ける浮力の大きさをfとすると以下のような図が書けます。何度も言いますが、まずは図を書けるようになることが1番です。
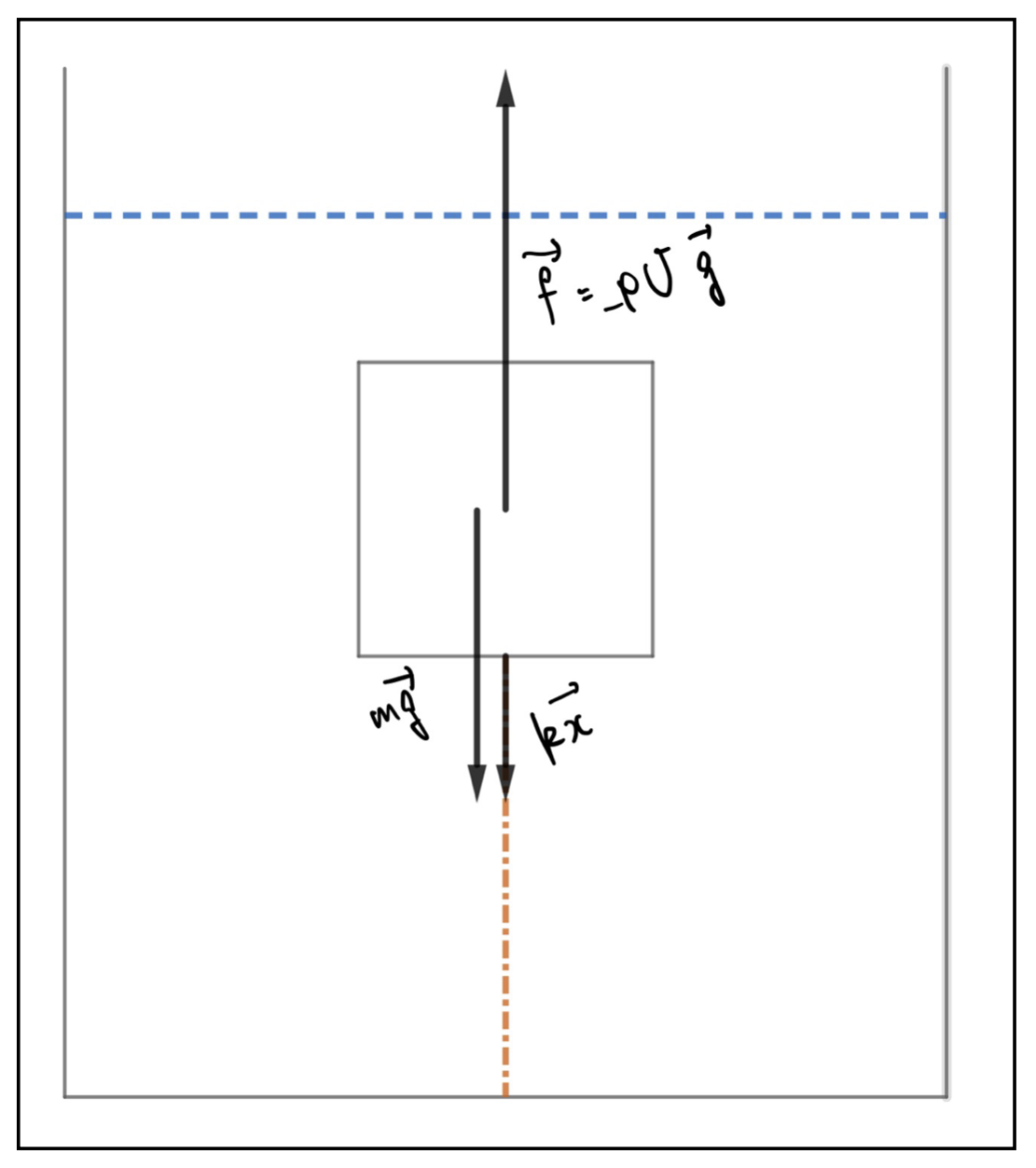
箱が静止していることから、上下方向に力がつりあっています。それぞれのベクトルの大きさを方向に注意して比べると
ここで、箱の質量は箱の密度と箱の体積の積で表されることを用いると、
となります。ばねの伸びをxとおいたので、xが正のときにはばねは伸びているし、負のときにはばねは縮んでいるということもすごく大事なポイントです。
水の密度の方が箱の密度よりも大きい場合にはばねは伸びます（＝箱は浮こうとしている）し、逆の場合にはばねは縮む（＝箱は沈もうとしている）わけですね。
氷が水に浮くのは氷の方が水よりも密度が小さいことをイメージし、この問題との対応を考えてもらうとなるほどと思う部分があるでしょうか？
問題
図のように角度\thetaの傾斜の、地面に固定された斜面の角に滑車がつけられていて、滑車を経由する伸び縮みしない糸によって質点Mと質点mが繋がれて静止している。
Mと斜面の間の静止摩擦係数は\muとするとき、mの質量によっては質点は動き出したり、静止したままの状態を保ったりする。
静止した状態を保つためにはmの質量の範囲はいくらになるか。
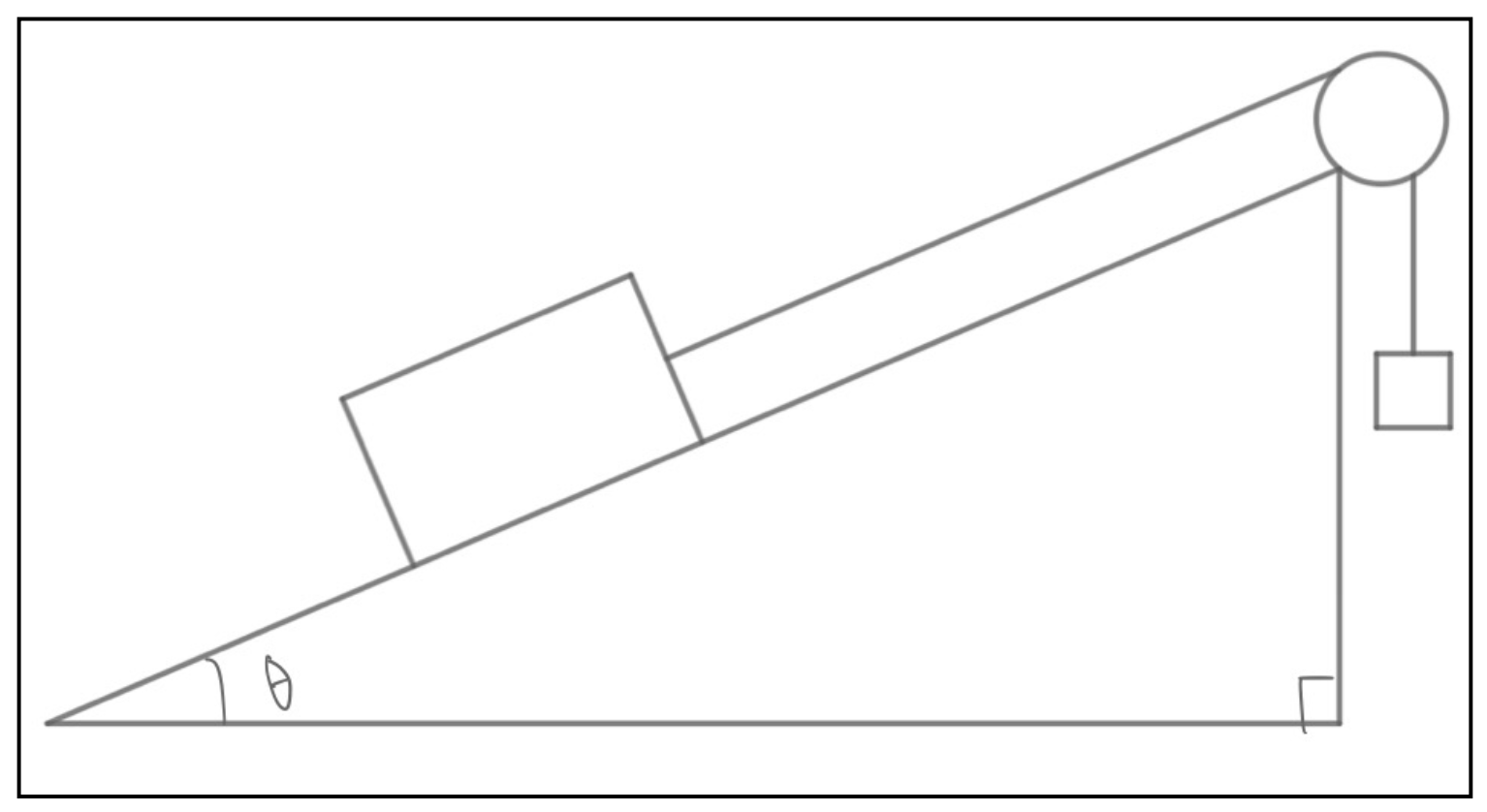
解答
張力をT、静止摩擦力をf、Mが斜面から受ける垂直抗力をNとして力を図示すると以下のような図になります。
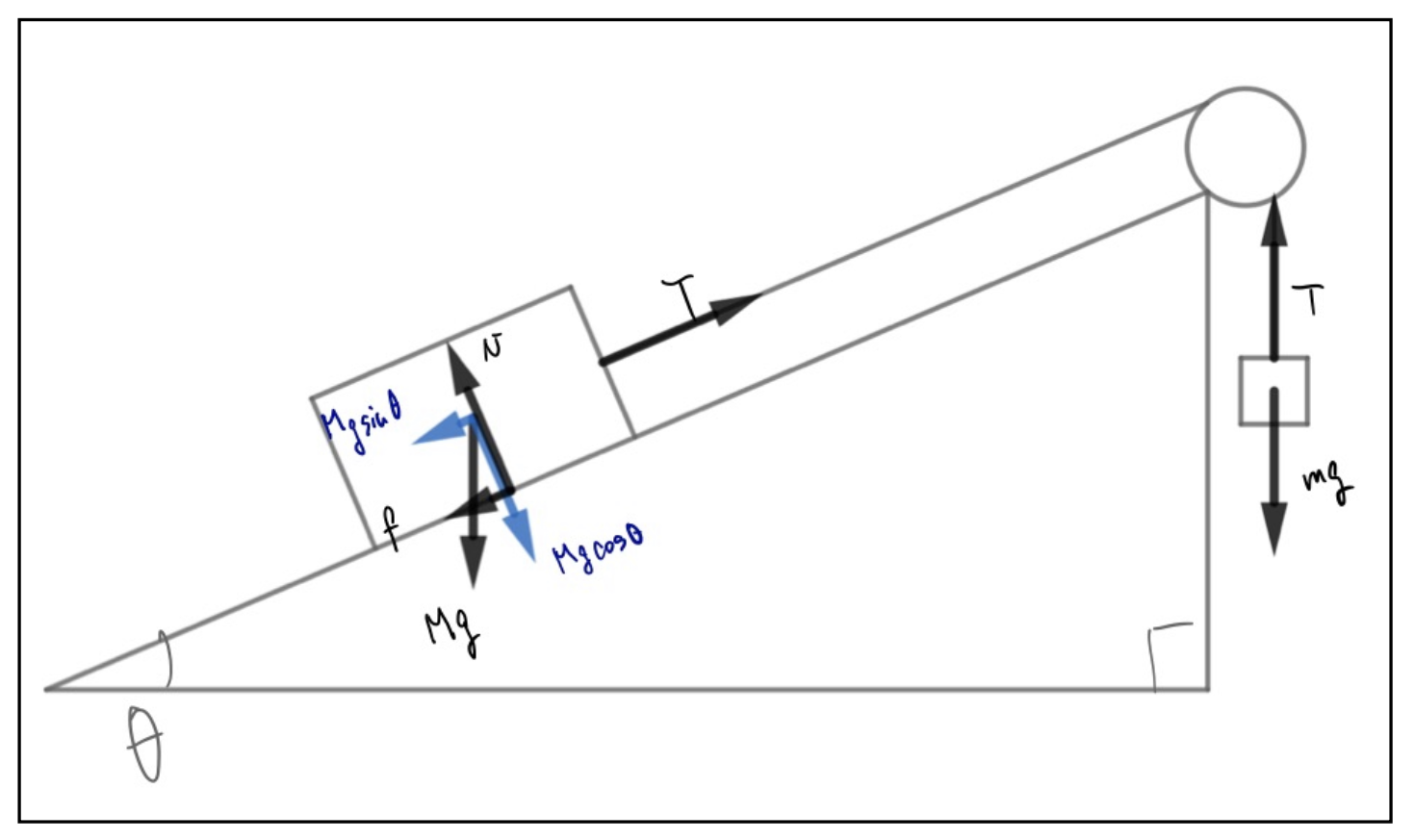
ただし、この図はmが重いためにMが上に動こうとしていて、それを妨げるように摩擦fが働いている場合です。
このとき、Mにかかる重力は斜面方向と斜面垂直方向に分解した方が計算の都合が良いので分解したものも書いておきました。細かい字になっていてすみません。
mもMも静止している場合には共に力のつりあい状態にあるのでそれを使っていくつか式を立てていきますね。まずmについては、以下のような式が得られます。
つづいて、Mの斜面に垂直な方向のつりあいは以下の式で表現されます。
さらにMの斜面に沿う方向のつりあいから、
この最後の式をfについて解くと、
ここで最初に書いた式つかってTを消去しました。この静止摩擦力の最大値がμとNの積で決まるので、
これをmについて解けばmの範囲がわかりますね。
さて、このmに対する不等式はmが重すぎると、Mが斜面の上方に滑り出してしまうことを示しています。
今度は逆にmが軽い場合を考えてみましょう。mが軽すぎるとMは斜面の下方へと滑り出してしまうのは感覚的にわかりますよね？
これを考えるためには、先ほどの図のfの向きを逆向きにすればいいだけです。式としては先ほどのfの符号を逆にすればいいだけなので、以下のようになります。
あとは全く同じように解くだけなので、最終的には以下のような不等式が導けます。
これでmの下限が決まったことになります。ここまでをまとめると以下のようになります。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」
東大理系攻略法を
解説したPDF販売中！
中高一貫校に行かなくても、塾に行かなくても、独学で受かるための勉強法を完全解説！
全科目の参考書
全参考書の使い方
受験までの勉強スケジュール
が全てわかります！
今だけ！100様限定60%OFF！
さらに24時間以内なら返金保証つき！
無料サンプル公開！
