(※数式が見切れている場合は横スクロールしてください。)
ここまでは基本的には質点の動きを見てきました。
ですが物体は質点だけではありません。というかむしろ質点の方が物理を考えるためだけの理想的なものですから、ここから考える剛体というものの方が自然なものです。
さて、剛体とはなんぞやということですが、ここでは運動の最中に形を変えないものと思っておいてください。
もちろん、運動の最中に形を変えるものの方が世の中では自然なものです。
どれだけ固いものでも、ギュッと強い力をかければ変形するのは普通ですからね。
ただ物体の変形まで取り扱うのは大変なので、ここでも変形はしないという条件を課したまま議論を進めていきます。
ちなみに、質点のときには大きさが無視できるもので回転というものをそれ自体の回転というものを考えていませんでした。
ここまで「つり合い」の状況というのは、力の合力がつり合っている状況だけを考えていました。しかし、本当に正しいものを考えようと思うと「回転しない」ことも条件として入れておかないといけないことは、すぐにわかります。
たとえば、次のような長方形に外力として\(\vec{F_1}\)と\(\vec{F_2}\)を加えたとしましょう。
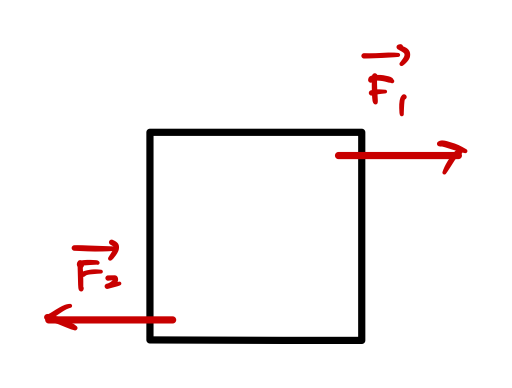
\(\vec{F_1}\)と\(\vec{F_2}\)の合力に関して言えば、\(\vec{0}\)でも回転は始めますよね。
本当に静止する状態を目指そうと思ったら、「並進しないこと=重心が動かないこと」と「回転しないこと」がポイントになります。
剛体を次のような質点同士が質量の無視できる固い棒でつながっているものとしましょう。
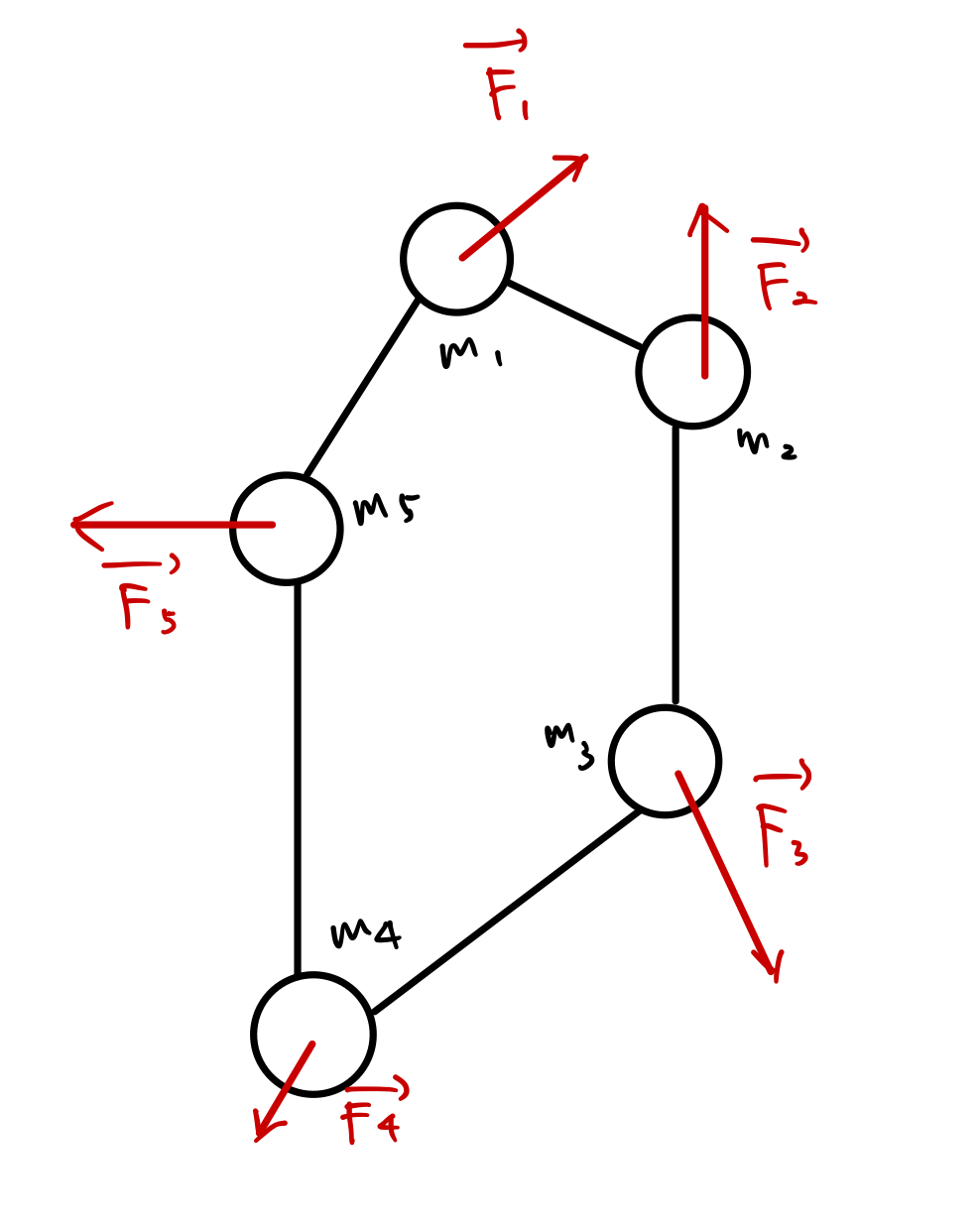
運動量の時間微分がゼロであれば、初期条件として運動量がゼロなら静止状態が続きます。
\dot{\vec{p}}=(m_1+m_2+m_3+\dots)\dot{\vec{v}}=\vec{F_1}+\vec{F_2}+\vec{F_3}+\dots
\end{align}
左辺は合計の運動量です。\(\vec{v}\)は剛体の速度です。この右辺の\(\vec{F_1},\vec{F_2},\dots\)は各質点にかかる合力を表しています。
これは結局全体にかかる力の合力がゼロというのが剛体の運動量の変化がゼロということになります。
次に回転に関して考えましょう。この剛体が回転していないとすると、どこ中心の角運動量でも、その時間微分はゼロになります。たとえば、各質点の重心から計った位置を\(\vec{x_1},\vec{x_2},\dots\)とします。
\dot{\vec{L}}=&(m_1+m_2+\dots)\vec{v}\times\vec{v}+(m_1\vec{x_1}+m_2\vec{x_2}+\dots)\times\dot{\vec{v}}\\
=&\vec{x_1}\times m_1\ddot{\vec{x_1}}+\vec{x_2}\times m_2\ddot{\vec{x_2}}+\dots\\
=&\vec{x_1}\times\vec{F_1}+\vec{x_2}\times\vec{F_2}+\dots
\end{align}
結局、各点のモーメントの和がゼロなら、回転を始めないということになりますね。
この式の計算が怪しいようなら、数学準備#9あたりを少し復習しておくといいですね。
ではここまでを踏まえて以下のような例を考えてみましょう。
例
摩擦のないなめらかな壁と、摩擦のある床とにかけて剛体の棒を立てかけたとする。棒の質量を\(M\)、棒の長さを\(l\)、床の静止摩擦係数を\(\mu\)、とする。
図のように角度\(\theta\)をとるとき、立てかけたまま静止する最大の角度\(\theta\)を求めよ。
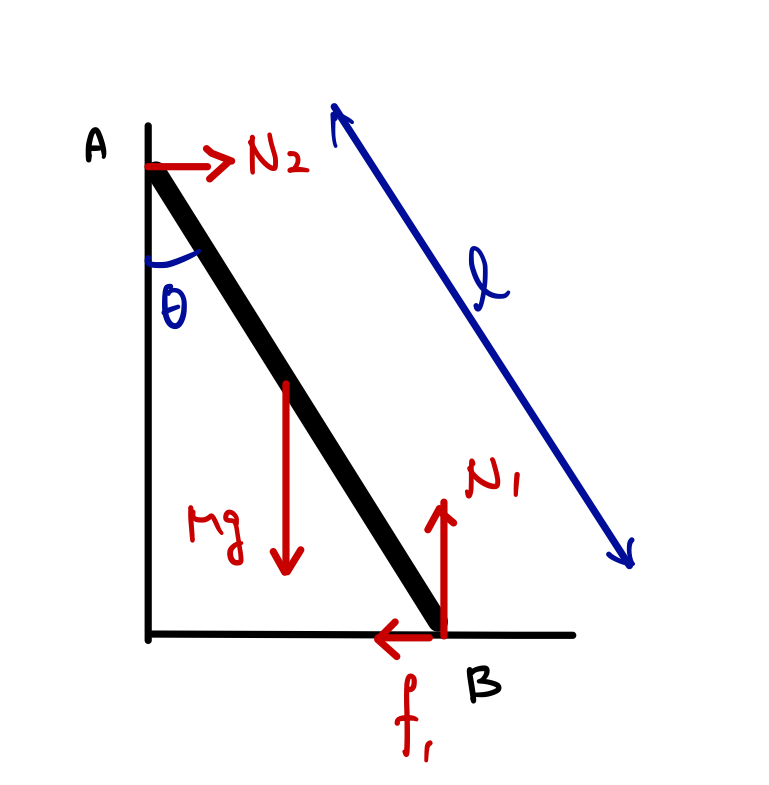
棒にかかる力を諸々、図に書いてみました。
まず並進運動しない(合力がゼロ)という条件を書き出してみると以下のようになります。
&f_1=N_2\\
&N_1=Mg
\end{align}
あとは回転しないという条件を計算しなければなりません。
回転軸の選び方は自由です。なぜなら、静止しているときにはどこを回転軸にしても、回転はしないですからね。
例えば、Aを回転軸にした場合にはモーメントの合計は以下のようになります。(右回転成分を正、左回転成分を負としました。)
\frac{l}{2}Mg\sin\theta+lf_1\cos\theta-lN_1\sin\theta=0
\end{align}
Bを回転軸にした場合にはモーメントの合計は以下のようになります。（今度は左回転の成分を正、右回転の成分を負としました。）
\frac{l}{2}Mg\sin\theta-lN_2\cos\theta=0
\end{align}
どちらを使っても同じ計算ができます。
ギリギリの角度を調べるときには、静止摩擦力の最大値と比較すればいいわけです。
簡単な計算から、
&\frac{Mg}{2}\tan\theta=f_1\leq\mu Mg\\
\Longleftrightarrow
&\tan\theta\leq 2\mu
\end{align}
この\(\theta\)が最大の角度となります。
高校物理の範囲で言えば、回転に関しては、「静止」している状態しか扱わないでいいので、ここまで理解できていれば問題ありません。
剛体が回転を伴った運動をするというのは大学の物理の範囲なので、興味がある方は先々まで進んで勉強する必要があります。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」
東大理系攻略法を
解説したPDF販売中！
中高一貫校に行かなくても、塾に行かなくても、独学で受かるための勉強法を完全解説！
全科目の参考書
全参考書の使い方
受験までの勉強スケジュール
が全てわかります！
今だけ！100様限定60%OFF！
さらに24時間以内なら返金保証つき！
無料サンプル公開！
