(※数式が見切れている場合は横スクロールしてください。)
ようやく物理っぽいことをマキノさんに教えられるところまで来ました。ここからは加速していきますよ。
ここからしばらくは1次元上（直線上）を質点が運動している場合を考えることにします。後々、3次元に拡張していきますが、最初は簡単な1次元からいきましょう。
直線上に目盛りを打って、各時刻ごとに質点の位置を記録していけば、質点の位置\(x\)を時刻の関数\(x(t)\)で表すことができますね。
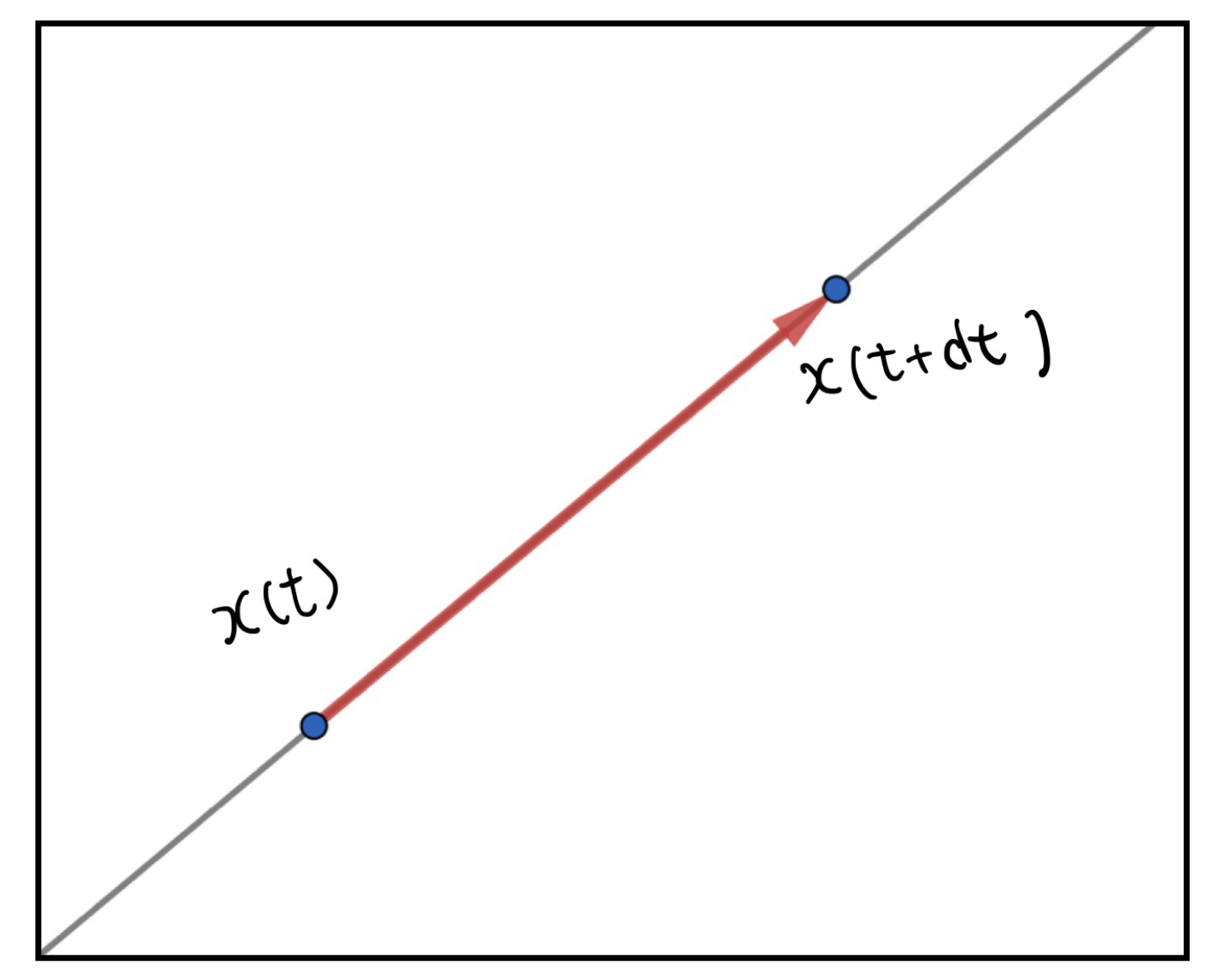
時刻が\(t\)のときの質点の位置を\(x(t)\)時刻が\((t+dt)\)の時の質点の位置を\(x(t+dt)\)とすると、このとき時間\(dt\)の間の平均の速度は、
\frac{x(t+dt)-x(t)}{dt}
\end{align}
となりますね。これは中学生でもわかる速さの求め方です。
平均の速度はあくまでも\(dt\)の間での平均であり、この値が時刻\(t\)での速度に一致する必要もないですし、時刻\((t+dt)\)での速度に一致する必要もありませんよね。
この\(dt\)の時間幅を段々と短くしていくと、時刻\(t\)での瞬間の速度\(v(t)\)に徐々に近づいていきます。\(dt\to0\)の極限では、時刻tでの瞬間の速度に完全に一致します。各時刻\(t\)での瞬間の速度\(v(t)\)は以下のように与えられます。ちなみにこれは微分の定義そのものなんです。
定義
v(t)=\lim_{dt\to0}\frac{x(t+dt)-x(t)}{dt}=\frac{d}{dt}x(t)
\end{align}
早速、前の章で習った微分のテクニックが出てきました。
位置が時刻の関数で与えられているときには、時間微分することによって、速度の関数を得ることができるんです。
さてさて、今度は速度の変化に目を向けてみましょう。
質点が車のようなものだと思うと、アクセルを踏めば速度は大きくなりますし、ブレーキを踏めば速度は小さくなります。
時刻\(t\)から時刻\((t+dt)\)の間に速度はどれくらい変わったかは以下の式で計算できます。
\frac{v(t+dt)-v(t)}{dt}
\end{align}
これも平均の加速度と言います。やはりこの変化も平均の加速度の極限\((dt\to0)\)によって瞬間瞬間の速度の変化を記述することができて、その瞬間瞬間の速度の変化のことを加速度といいます。
定義
a(t)=\lim_{dt\to0}\frac{v(t+dt)-v(t)}{dt}=\frac{d}{dt}v(t)
\end{align}
物理においては時間微分を上付きのドットで表現することも多いです。以下の表現の仕方も覚えておいてください。
定義
\begin{cases}
v(t)=\frac{d}{dt}x(t)=\dot{x}(t)\\
a(t)=\frac{d}{dt}v(t)=\dot{v}(t)=\frac{d^2}{dt^2}x(t)=\ddot{x}(t)
\end{cases}
\end{align}
ここまでの流れをまとめると、
- 各時刻ごとに位置\(x\)を測定し、位置を時刻\(t\)の関数\(x(t)\)として表す。
- \(x(t)\)を微分することで、速度の関数\(v(t)\)を得る。
- 速度の関数\(v(t)\)を微分することで加速度の関数\(a(t)\)を得る。
このようにひとたび、位置の関数\(x(t)\)を得れば、微分操作をすることによって速度と加速度の関数を得ることができることがわかります。
問題
位置の関数が以下のように与えられたときの、速度と加速度の関数を求めよ。
x(t)=At^2+Bt+C
\end{align}
解答
&v(t)=\dot{x}(t)=2At+B\\
&a(t)=\dot{v}(t)=2A
\end{align}
ちなみにここで扱った位置、速度、加速度、そして時刻は基本的には、メートルと秒を使っていると思ってください。物理でよく使われるのはメートルと秒です。
ここまで来ると今度は次のようなことを考えたくなります。
- 加速度や、速度の関数が与えられたときに、位置の関数を得ることは可能なのか？
- 加速度の源は何か？
これらを考えるために、まずは数学の準備をすることにしましょう。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」
東大理系攻略法を
解説したPDF販売中！
中高一貫校に行かなくても、塾に行かなくても、独学で受かるための勉強法を完全解説！
全科目の参考書
全参考書の使い方
受験までの勉強スケジュール
が全てわかります！
今だけ！100様限定60%OFF！
さらに24時間以内なら返金保証つき！
無料サンプル公開！
