(※数式が見切れている場合は横スクロールしてください。)
運動量の保存則を以前扱いましたので、角運動量の保存則も使っておきましょう。
質点の原点周りの角運動量の時間微分は以下のようになることを見ました。
\frac{d}{dt}\vec{L}(t)=\vec{x}(t)\times\vec{F}(t)
\end{align}
これをある時刻\(t_1\)から\(t_2\)まで積分すれば、その時刻間の角運動量の変化を計算することができます。今の段階では、右辺の\(\vec{x}\times\vec{F}\)が時間によらず\(\vec{0}\)になっている状況だけ扱えるとそれで十分です。
外積の定義から\(\vec{x}\times\vec{x}=\vec{0}\)ですから、\(\vec{F}=k\vec{x}\)の関係が時間によらず成り立っていれば、角運動量は保存することがわかります。
\(\vec{F}=k\vec{x}\)となるような力を中心力と言います。中心力によって円運動している質点の問題を1つ見ておきましょう。
問題
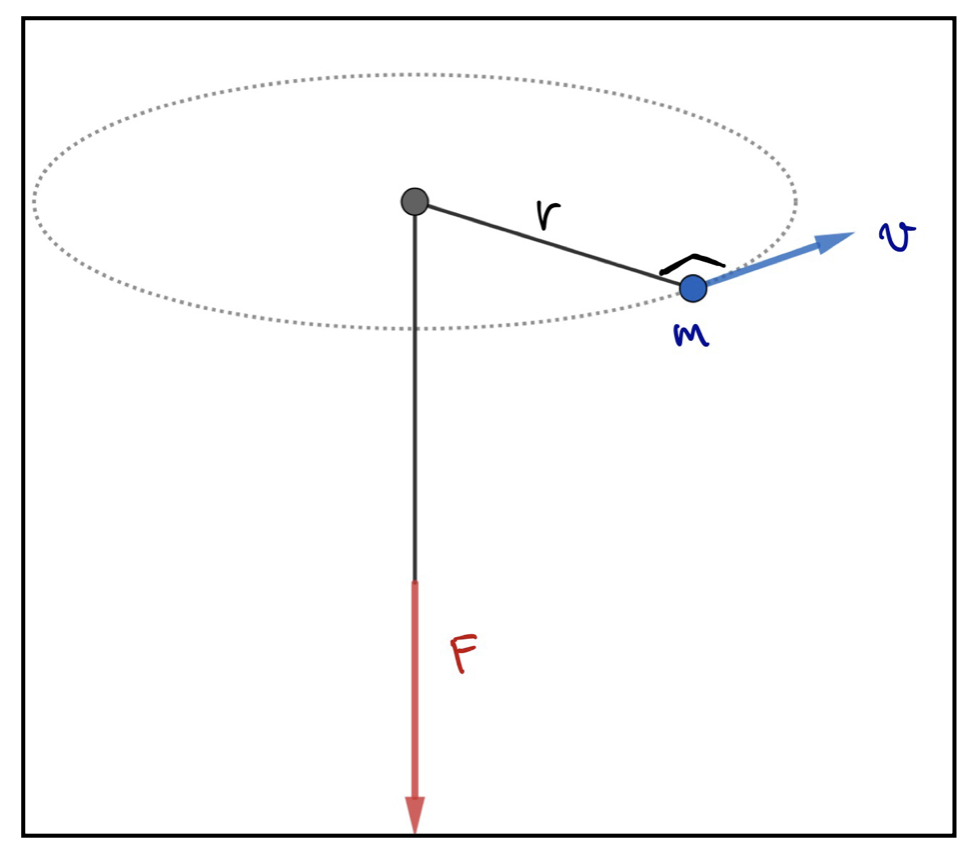
以下の図のように摩擦のない板に穴を開け、そこに糸を通して、板を水平に固定する。板の上面にある方の糸の端に質点mをくっつけて、逆の端に、一定の外力\(F\)を板に対して垂直に下向きに加える。この間、質点は図のように半径\(r\)、速さ\(v\)で等速円運動をしていた。
1.
このとき質点の中心の穴周りの角運動量の大きさを求めよ。
2.
糸をゆっくり引いて円運動の半径を\(r’\)にしたとき、質点の速さはいくらになるか求めよ。
3.
半径を\(r\)から\(r’\)にしたときに外力がした仕事を求めよ。
解答
1.
等速円運動のときには、\(\vec{x}\)と\(\vec{v}\)が垂直になるのでした。よって角運動量の大きさはすぐに求められます。
\left|\vec{L}\right|=\left|\vec{x}\right|\cdot m\left|\vec{v}\right|=mrv
\end{align}
2.
質点が受けているのは中心力ですから、角運動量は保存します。すなわち求めたい速さを\(v’\)とすると以下の式が成り立ちます。
&mrv=mr’v’\\
\Longleftrightarrow
&v’=\frac{rv}{r’}
\end{align}
3.
ゆっくり糸を引いているので、各瞬間ごとに円運動の状態は保っていると考えます。
半径\(r’\)速さ\(v’\)の円運動の向心力が外力の大きさになるはすですね。
F=m\frac{v’^2}{r’}=m\frac{r^2v^2}{r’^3}
\end{align}
この\(v’\)は全問の結果から、円運動の半径\(r’\)の関数ですので、外力\(F\)も\(r’\)の関数として書けます。
この大きさで力の方向に沿って引くので、外力のした仕事は以下のように計算できます。原点から離れる向きを正としたので、力は負で計算します。
-\int^{r’}_{r}m\frac{r^2v^2}{r’^3}dr’=&mr^2v^2\left[\frac{1}{2}r’^{-2}\right]^{r’}_{r}\\
=&\frac{m}{2}\cdot\frac{r^2v^2}{r’^2}-\frac{m}{2}v^2\\
=&\frac{m}{2}v’^2-\frac{m}{2}v^2
\end{align}
結局、運動エネルギーの変化ぶんだけ外力は仕事すればいいわけですね。これはイメージ通りだなと思える状態だと嬉しいですね。
自信がなければエネルギー保存則のところを復習しておいてくださいね。
この問題だと、質点にかかるのは中心力だけなので、角運動量が保存します。角運動量が保存するために、半径と速さの積が一定になります。
ゆっくり糸を引いて、質点に仕事を与えてやると、その分が運動エネルギーの変化になって速さが大きくなります。
速さが大きくなるということは半径は小さくなるということですね。速さと半径の関係が反比例の関係になっているのは面白い例ですね。
実はフィギュアスケートのスピンとの対応をこの問題から考察できるのですが、どうでしょうか？少し考えてみてください。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」
東大理系攻略法を
解説したPDF販売中！
中高一貫校に行かなくても、塾に行かなくても、独学で受かるための勉強法を完全解説！
全科目の参考書
全参考書の使い方
受験までの勉強スケジュール
が全てわかります！
今だけ！100様限定60%OFF！
さらに24時間以内なら返金保証つき！
無料サンプル公開！
