三角関数｜ぽこラボ勉強ブログ

(※数式が見切れている場合は横スクロールしてください。)

三角関数はある角度を入力するとそれに応じた値を返してくれる関数です。初等的な物理で使う頻度が一番高いのは\(0\)［rad.］から\(\pi/2\)［rad.］の間に収まる角度を入力した三角関数です。まずはそこから解説していくことにしますね。

あ、ちなみに最初だけrad.をわざわざ表記しましたけど、ここからは書きませんからね。置いていかれないようにrad.を意識しておいてくださいよ、マキノさん。

以下のような直角三角形ABCを考えます。それぞれの辺の長さを図のように\(a,b,c\)とし、角Bの大きさを\(\theta\)（シータもしくはテータと読む）としましょう。

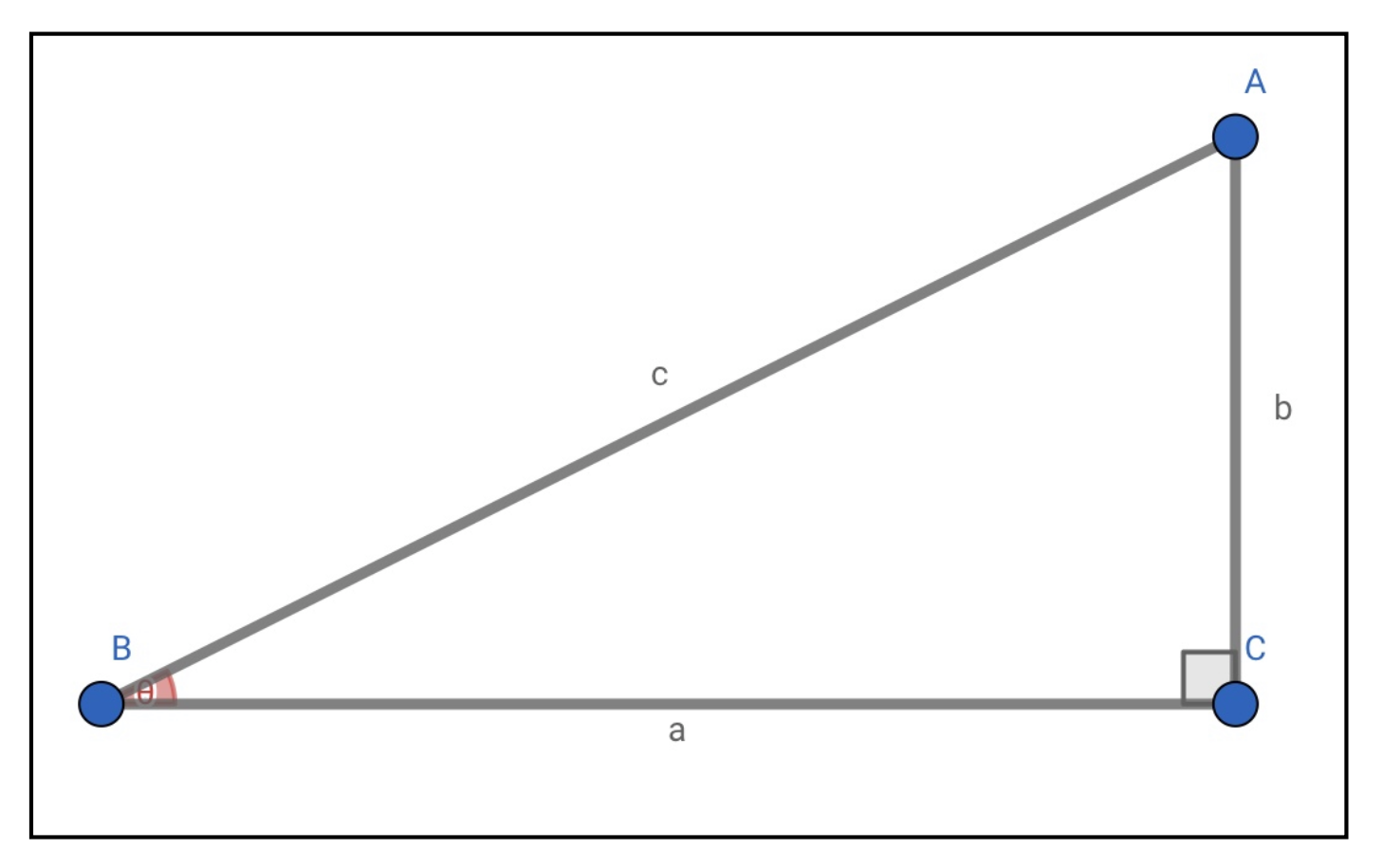
このときに三角関数を次のように定義します。（この段階では三角比と表現した方が適切かもしれません。）

定義

各三角関数の名前を\(\sin,\cos,\tan\)とし、その後ろに来る角度をその関数の引き数として、以下のように定義する。

\begin{align}
&\cos\theta=\frac{a}{c}\\
&\sin\theta=\frac{b}{c}\\
&\tan\theta=\frac{b}{a}
\end{align}

大事なことは、直角三角形の直角の位置と\(\theta\)の位置関係、それに対応する辺の位置と長さなんかもろもろ合わせて、三角関数は定義されるということです。

ですから、この直角三角形が回転していても同じように三角関数が使えるようになっておくのが大事です。

ここで、物理で使う形に慣れておくために問題をいくつか解いてもらうことにしましょう。

問題

以下の図の\(X\)、\(Y\)を\(Z\)と\(\theta\)を用いて表現せよ。
1.

解答

1.
三角関数の定義より、

\begin{align}
\sin\theta=\frac{X}{Z}
\end{align}

なので、これを変形して

\begin{align}
X=Z\sin\theta
\end{align}

同様に考えると

\begin{align}
Y=Z\cos\theta
\end{align}

2.
上の問題と同様に考えるとすぐにわかります。

\begin{align}
&X=\frac{Z}{\cos\theta}\\
&Y=Z\tan\theta
\end{align}

ここまでは直角三角形を用いた定義でした。この段階では三角関数と呼ぶよりは三角比と呼ぶことも多いですね。

直角三角形を用いて、直角とは違う\(\theta\)という角度を三角関数に代入して、値を得るという方法でした。この方法だと、\(\theta\)の範囲は\(0\)から\(\pi/2\)までしか適応できないです。

より一般の角度について定義できるように三角関数の定義を拡張することにしましょう。

拡張のためには半径\(1\)の円の方程式を利用します。半径\(1\)の円を単位円と言います。（ちなみに単位「」という単語が出てきたら、特徴的な長さが\(1\)の図形だと思うと大抵正しい定義になっています。）

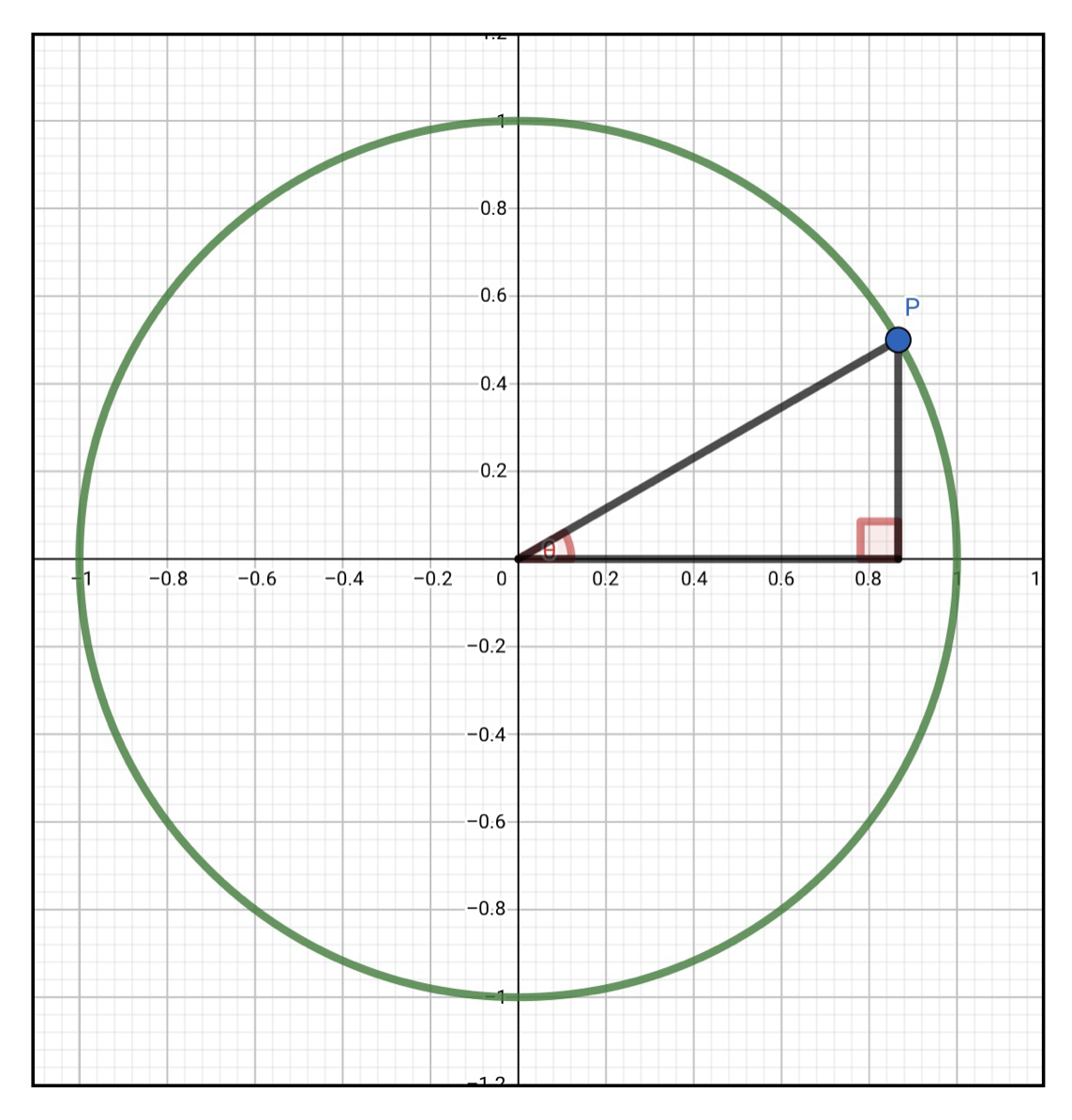
以下の図のように単位円上に点P\((x,y)\)を取って、直角三角形を作ってみます。

単位円の性質上、OPの長さは\(1\)なので、図の\(\theta\)を三角関数の引数に入れると以下のことがわかりますね。

\begin{align}
&\cos\theta=x/1=x\\
&\sin\theta=y/1=y\\
&\tan\theta=y/x
\end{align}

これを言葉で表すと、\(\cos\)はPのx座標、\(\sin\)はPのy座標、\(\tan\)は直線OPの傾きということになります。\(\theta\)が\(\pi/2\)よりも大きいときにもこの言葉通りの意味を使って三角関数を定義します。

定義

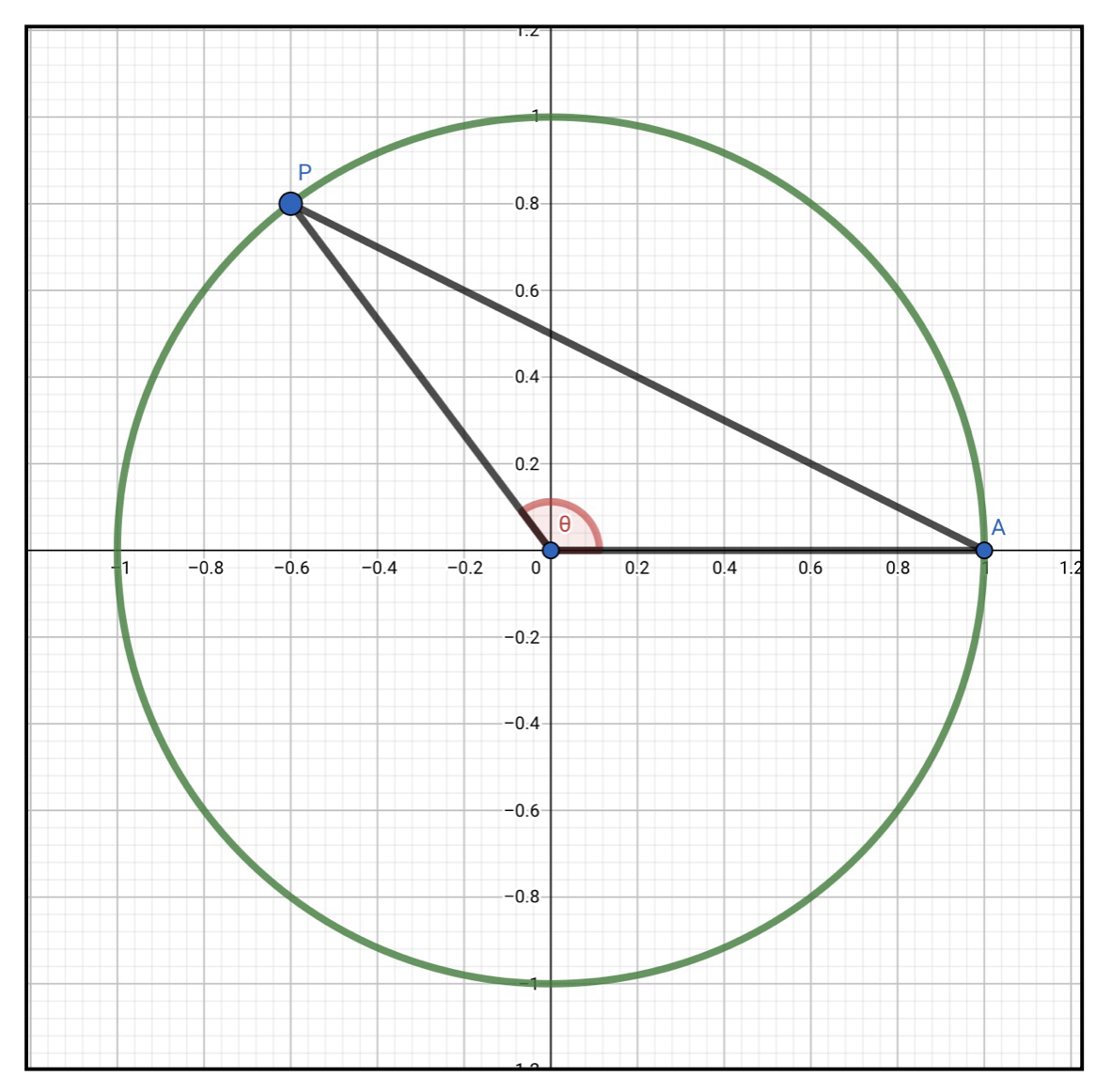
図のように点Pを単位円上におき、∠AOPを\(\theta\)とし、\(\theta\)は必ずOA側から反時計回りに測る時、

\(\cos\theta\)をPのx座標、\(\sin\theta\)をPのy座標、\(\tan\theta\)を直線OPの傾きで定義する。

このように定義すると\(\theta\)を\(\pi/2\)以上になったときも三角関数を定義できますね。いくつかよく使う公式を導いておくことにします。

点Pは単位円上にあるので、Pの座標\((x,y)\)は円の方程式を満たすので、以下の公式を導けますね。

\begin{align}
&x^2+y^2=1\\
\Longleftrightarrow&(\sin\theta)^2+(\cos\theta)^2=1
\end{align}

また、\(\tan\theta\)に関してはその定義から、

\begin{align}
\tan\theta=\frac{y}{x}=\frac{\sin\theta}{\cos\theta}
\end{align}

がわかります。最後に、公式の最初のものを\(\cos\)の2乗で割り算してまとめると、

\begin{align}
&\left(\frac{\sin\theta}{\cos\theta}\right)^2+1=\frac{1}{(\cos\theta)^2}\\
\Longleftrightarrow&(\tan\theta)^2+1=\frac{1}{(\cos\theta)^2}
\end{align}

公式

\begin{align}
&1.\quad(\sin\theta)^2+(\cos\theta)^2=1\\
&2.\quad\tan\theta=\frac{\sin\theta}{\cos\theta}\\
&3.\quad(\tan\theta)^2+1=\frac{1}{(\cos\theta)^2}\\
\end{align}

注意

三角関数は指数の付く位置によって意味が変わるので注意が必要なんです。

\begin{align}
&\sin^2\theta=(\sin\theta)^2\\
&\sin\theta^2=\sin(\theta^2)
\end{align}

前者は\(\sin\)に\(\theta\)を代入してから、返ってきた値を2乗、後者は\(\theta\)を2乗してから、\(\sin\)という関数に代入したものです。2乗に限らず一般のn乗について、同様の書き方を普通は用いるので覚えておいてください。

公式に慣れるために一つ問題を解いてみましょう。

問題

\(\cos\theta\)が\(1/2\)と与えられている時、\(\sin\theta\)と\(\tan\theta\)の値を求めよ。

解答

公式から、

\begin{align}
\sin^2\theta=&1-\cos^2\theta\\
=&1-\frac{1}{4}=\frac{3}{4}\\
\Longleftrightarrow\sin\theta=&\pm\frac{\sqrt{3}}{2}
\end{align}

このとき、\(\tan\theta\)は、

\begin{align}
\tan\theta=\frac{\cos\theta}{\sin\theta}=\frac{1/2}{\pm\sqrt{3}/2}=\pm\frac{1}{\sqrt{3}}
\end{align}

典型的な角度（弧度法の章で問題に出したような角度）に関しては有名な直角三角形の性質を使えば計算できます。

そしてそれらはパッと答えられるようになっておくことが好ましいです。暗記するくらいのつもりでちょうどいいと思ってください。

では図を見ながら一応確認しておきますね。

まず一つ目は\(30^{\circ}\)、すなわち\(\pi/6\)の系統ですね。

これらは、中学校で習う三平方の定理を使うとすぐ以下のような値が計算できます。（有名な\(1:2:\sqrt{3}\)の三角形です。）

\begin{align}
&\cos\frac{\pi}{6}=-\cos\frac{5\pi}{6}=-\cos\frac{7\pi}{6}=\cos\frac{11\pi}{6}=\frac{\sqrt{3}}{2}\\
&\sin\frac{\pi}{6}=\sin\frac{5\pi}{6}=-\sin\frac{7\pi}{6}=-\sin\frac{11\pi}{6}=\frac{1}{2}\\
&\tan\frac{\pi}{6}=-\tan\frac{5\pi}{6}=\tan\frac{7\pi}{6}=-\tan\frac{11\pi}{6}=\frac{1}{\sqrt{3}}
\end{align}

これらはいつでも使えるようにしておくといいですね。

次は\(45^{\circ}\)、すなわち\(\pi/4\)の系統です。

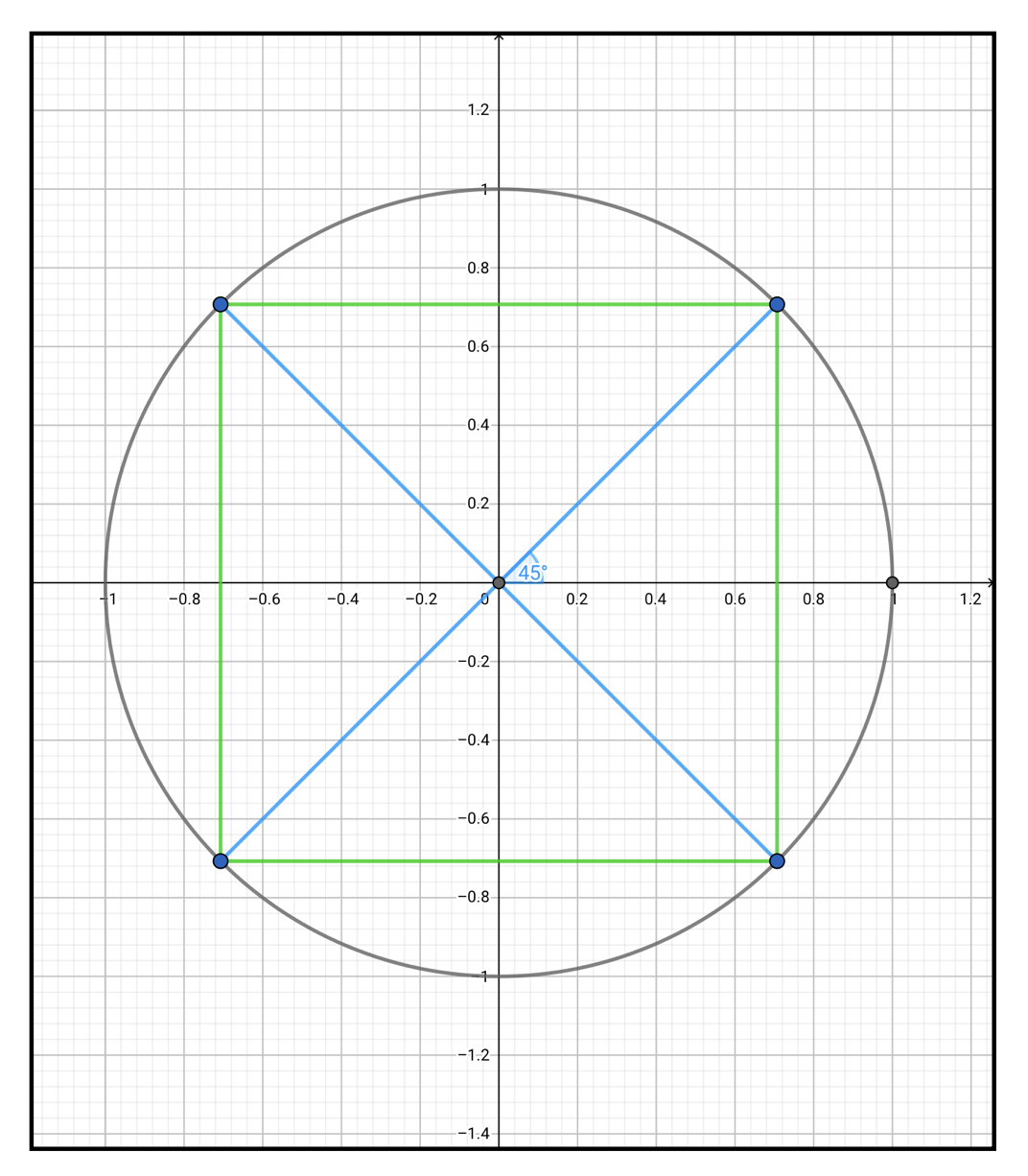
今度は\(1:1:\sqrt{2}\)の三角形を意識すると次のような値になることがわかります。

\begin{align}
&\cos\frac{\pi}{4}=-\cos\frac{3\pi}{4}=-\cos\frac{5\pi}{4}=\cos\frac{7\pi}{4}=\frac{1}{\sqrt{2}}\\
&\sin\frac{\pi}{4}=\sin\frac{3\pi}{4}=-\sin\frac{5\pi}{4}=-\sin\frac{7\pi}{4}=\frac{1}{\sqrt{2}}\\
&\tan\frac{\pi}{4}=-\tan\frac{3\pi}{4}=\tan\frac{5\pi}{4}=-\tan\frac{7\pi}{4}=1
\end{align}

次に\(60^{\circ}\)、すなわち\(\pi/3\)の系統です。

\begin{align}
&\cos\frac{\pi}{3}=-\cos\frac{2\pi}{3}=-\cos\frac{4\pi}{3}=\cos\frac{5\pi}{3}=\frac{1}{2}\\
&\sin\frac{\pi}{3}=\sin\frac{2\pi}{3}=-\sin\frac{4\pi}{3}=-\sin\frac{5\pi}{3}=\frac{\sqrt{3}}{2}\\
&\tan\frac{\pi}{3}=-\tan\frac{2\pi}{3}=\tan\frac{4\pi}{3}=-\tan\frac{5\pi}{3}=\sqrt{3}
\end{align}

最後に\(90^{\circ}\)、すなわち\(\pi/2\)の系統ですが、これらの角度は\(\tan\)の値に注意が必要です。\(tan\)の値が単位円周上の点と、原点を結ぶ直線の傾きなので、傾きを定義出来ないときには\(tan\)の値も定義できません。

\begin{align}
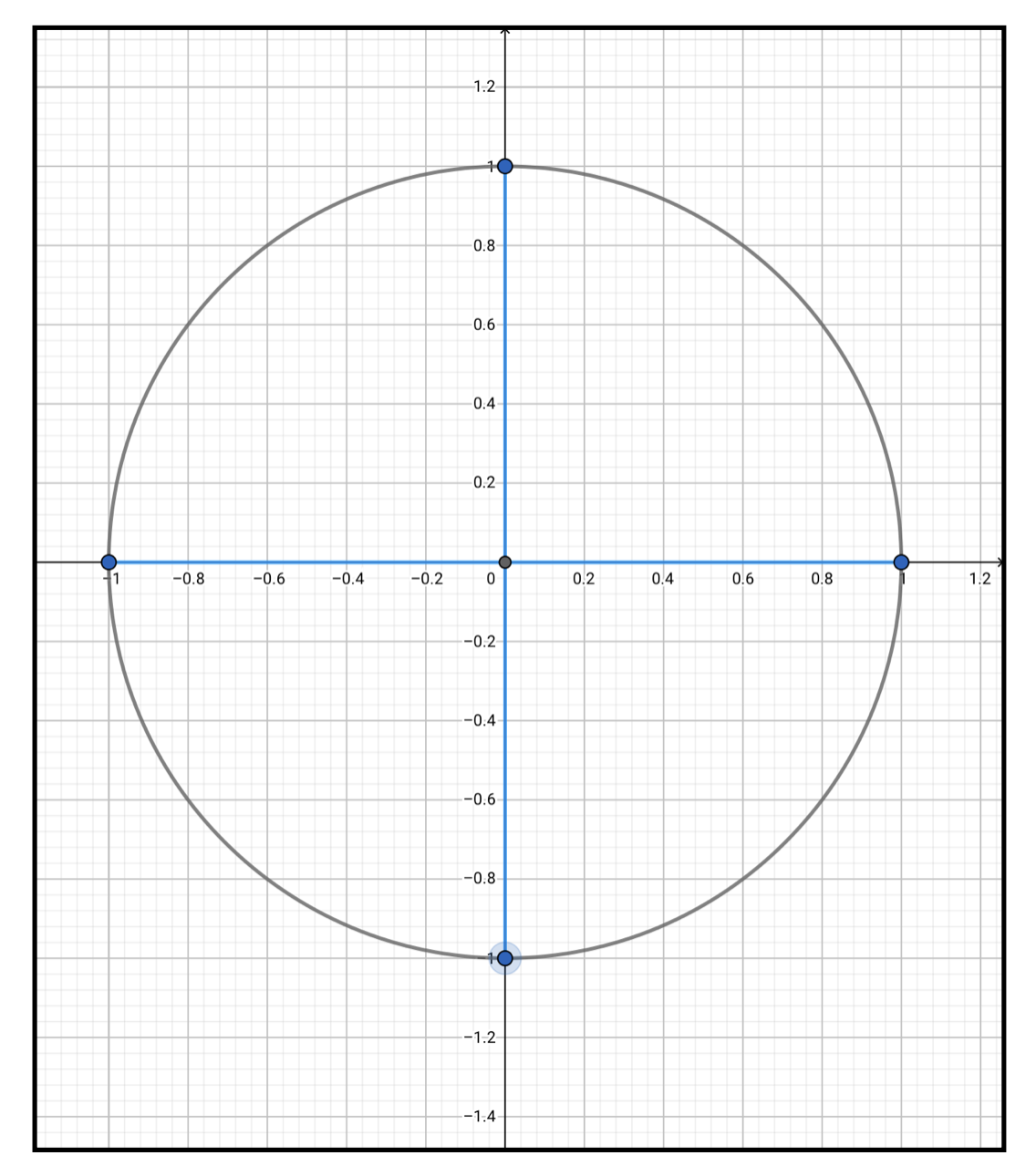
&\cos\frac{\pi}{2}=\cos\frac{3\pi}{2}=\sin0=\sin\pi=0\\
&\sin\frac{\pi}{2}=-\sin\frac{3\pi}{2}=\cos0=-\cos\pi=1\\
&\tan0=\tan\pi=0\\
&\tan\frac{\pi}{2}=\tan\frac{3\pi}{2}=\times
\end{align}

関連リンク

>>ブログ版アラサー高校物理の記事一覧

>>物理の勉強ロードマップ【2019年版】

>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」