ベクトルの分解｜ぽこラボ勉強ブログ

(※数式が見切れている場合は横スクロールしてください。)

先ほどの節では、2つのベクトルに対して図形的処理を施して、1つのベクトルに合成することを学びましたね。

今度は逆向きの処理を学びます。つまり、1つのベクトルに平行四辺形（ほとんどの場合は長方形）を用いた図形的処理を施して、2つのベクトルに分解するという作業をできるようになってもらいましょうってことです。

物理の勉強は特に、このベクトルの分解の作業ができるようになっておくことが重要ですよ。この節が終わればまた力学の説に戻れますからね。もうひと頑張りです。

例として斜面上の物体に、ベクトルで表される力がかかっている場合を考えましょう。（力はベクトルで表現できるという話をしましたね。）

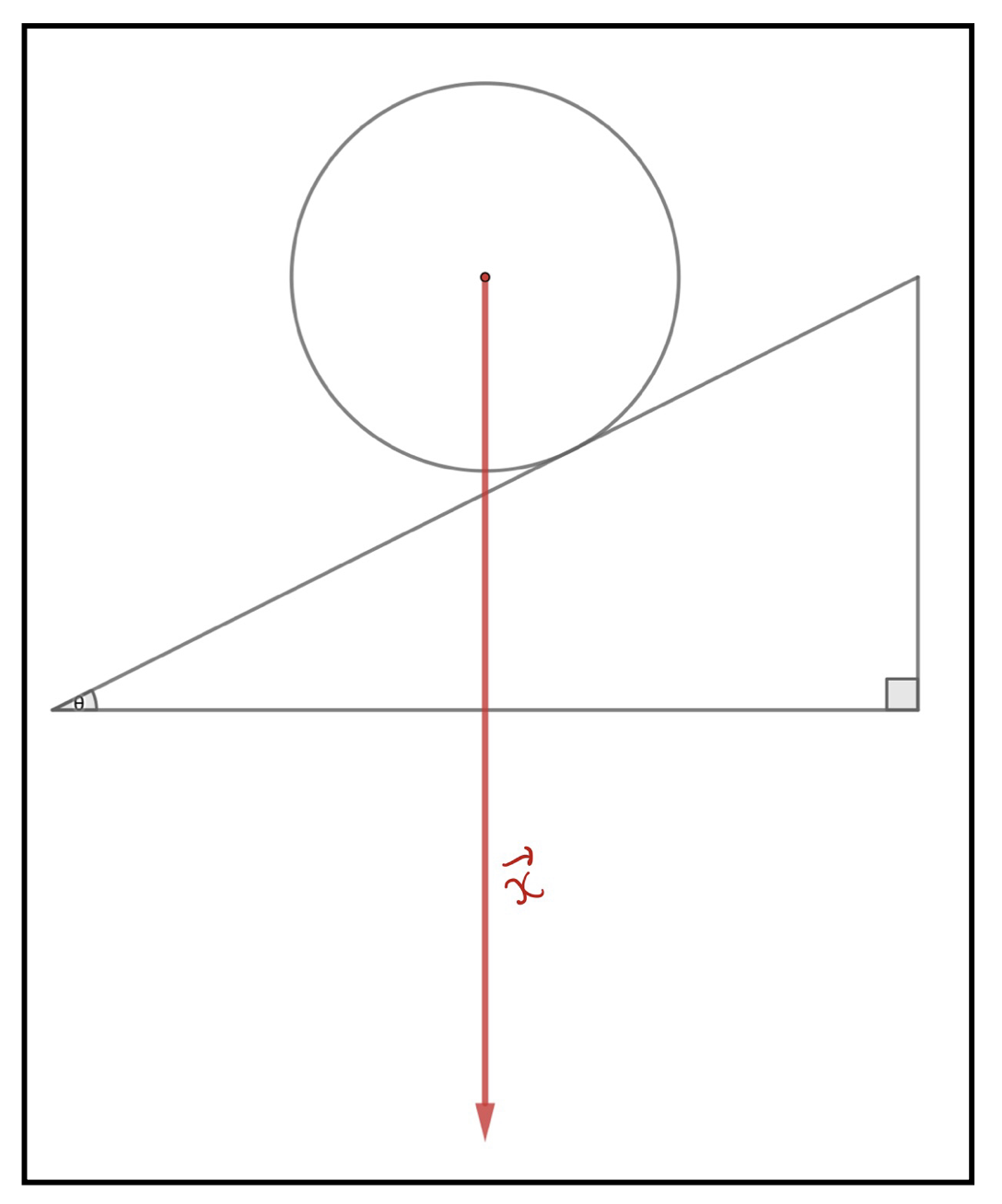
この\(\vec{x}\)を斜面と平行な方向と斜面に垂直な方向の2つのベクトルに分解することを考えるのが今回の課題です。

下の図のように\(\vec{x}\)を対角線に持ち、各辺が斜面に平行な方向と垂直な方向になるような長方形を作ります。

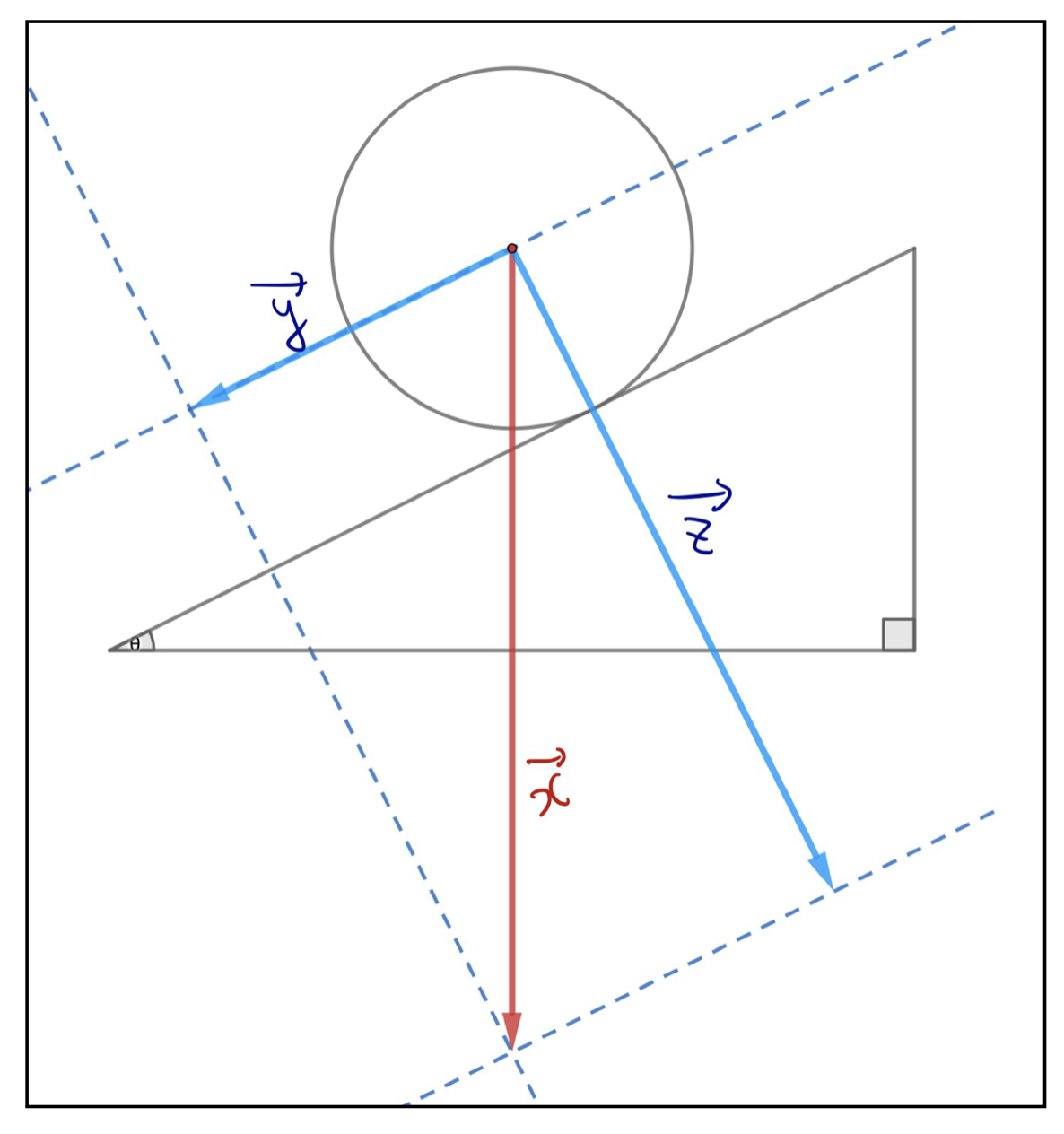
その辺に沿ってベクトルを分解すると上図のように2つのベクトルを使って以下のように書くことができます。

\begin{align}
\vec{x}=\vec{y}+\vec{z}
\end{align}

このように分解した、ふたつのそれぞれのベクトルの大きさはいくらになるか、というのも計算することができます。

というか、それを計算できるようになるために三角関数の準備をしていたんですけどね。。。

それぞれのベクトルの大きさは、以下のように斜面の傾きを司るパラメータ\(\theta\)を用いて表現できることがわかります。

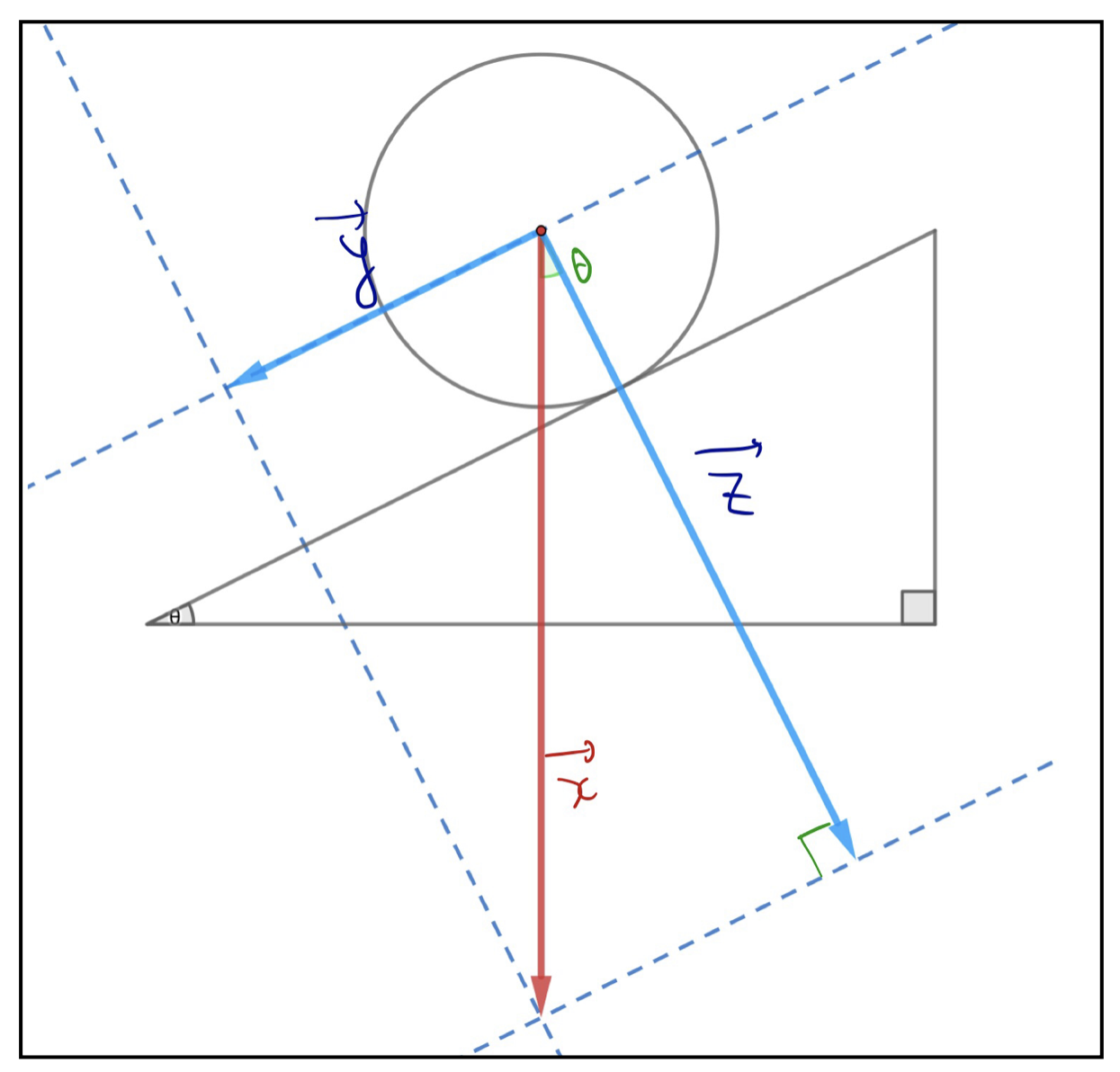
ベクトルの大きさをふたつの縦棒||でベクトルを挟む表現を使うと（一般的な表記の方法です）、

\begin{align}
&\left|\vec{y}\right|=\left|\vec{x}\right|\sin\theta\\
&\left|\vec{z}\right|=\left|\vec{x}\right|\cos\theta\\
\end{align}

と、いう風に表現することができます。

あとは問題で少しベクトルの分解に慣れておいてもらいましょう。

問題

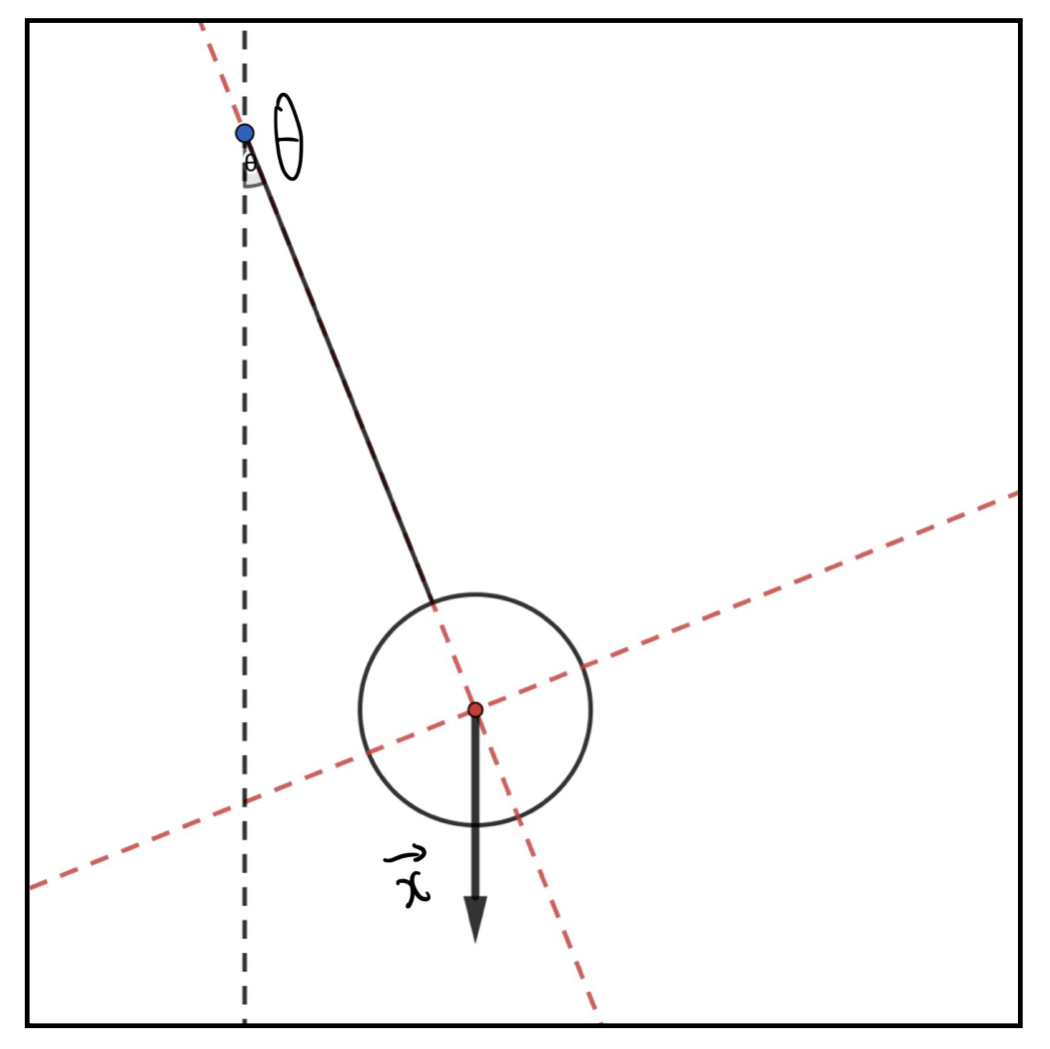
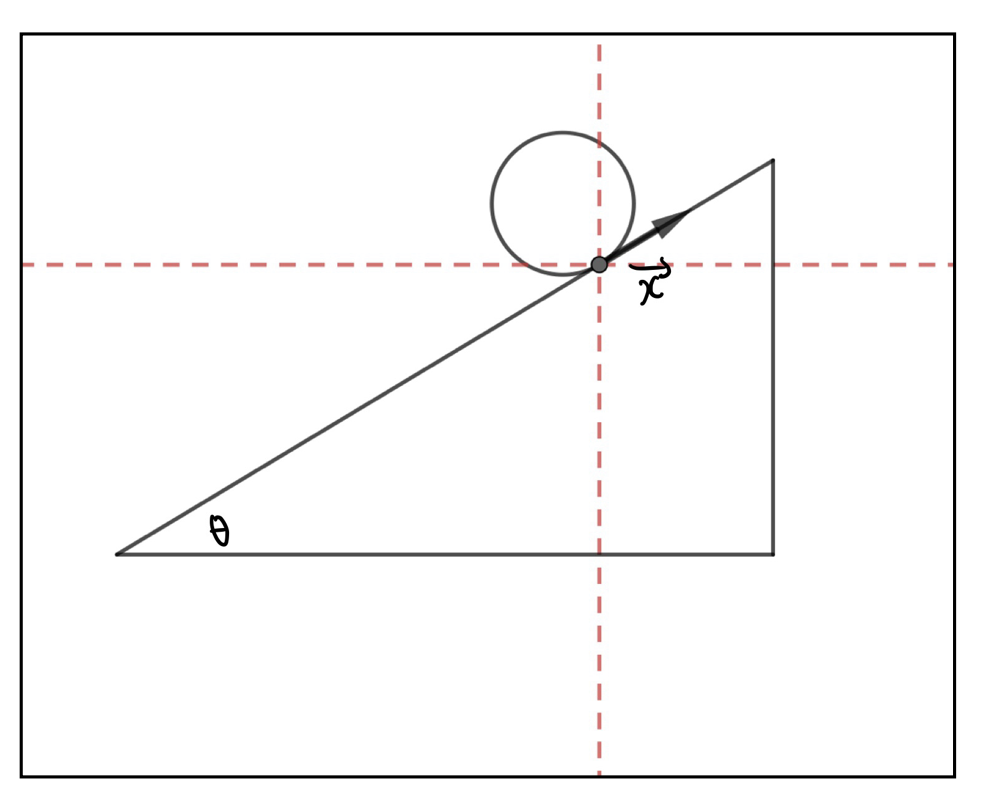
指定された方向（赤点線の方向）へ\(\vec{x}\)を分解せよ。

解答

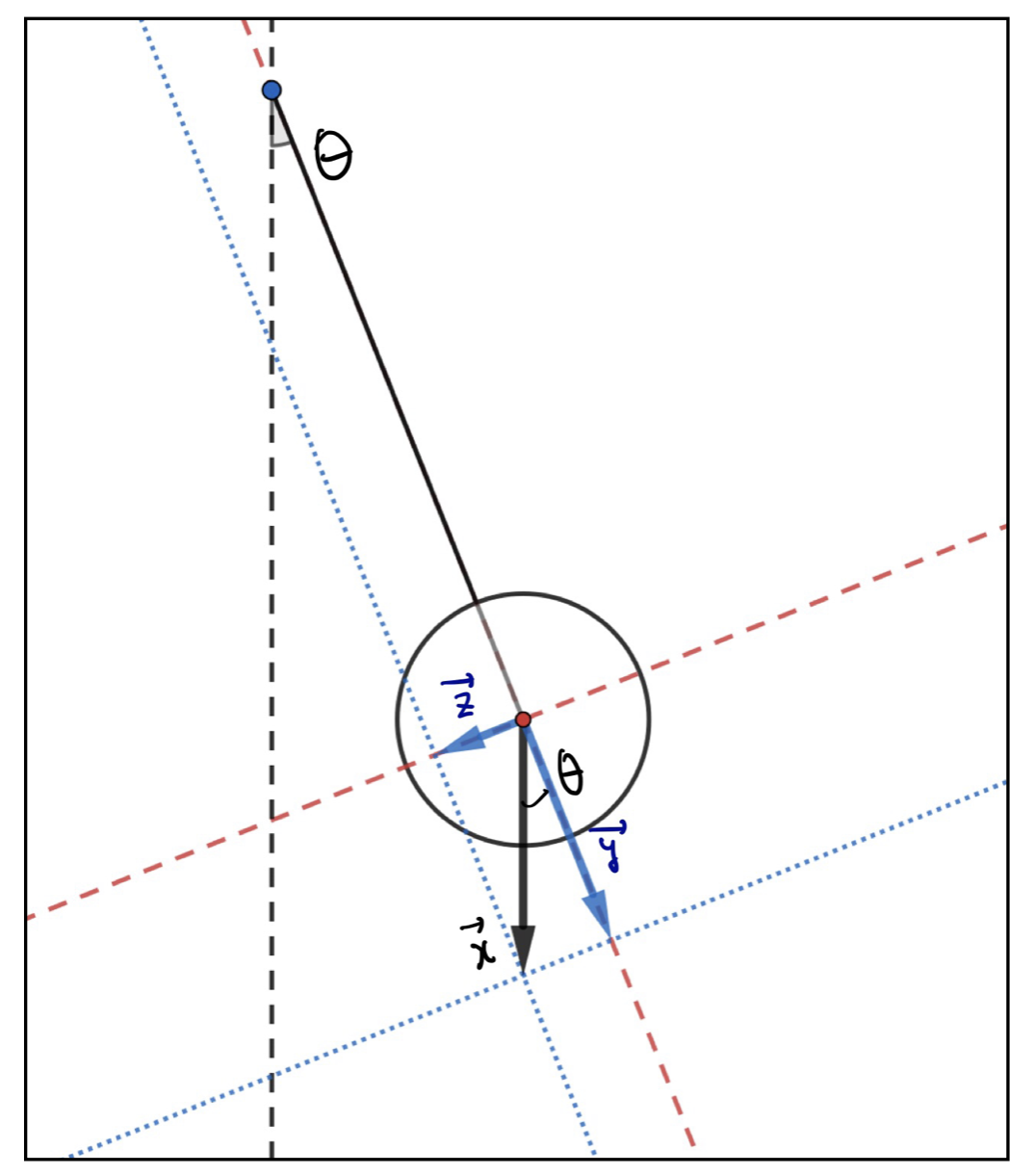
1.
実はこの問題は振り子にかかる重力をイメージした問題です。ここまでの解説通りに考えると以下のように分解できます。

\begin{align}
&\vec{x}=\vec{y}+\vec{z}\\
&\left|\vec{y}\right|=\left|\vec{x}\right|\cos\theta\\
&\left|\vec{z}\right|=\left|\vec{x}\right|\sin\theta\\
\end{align}

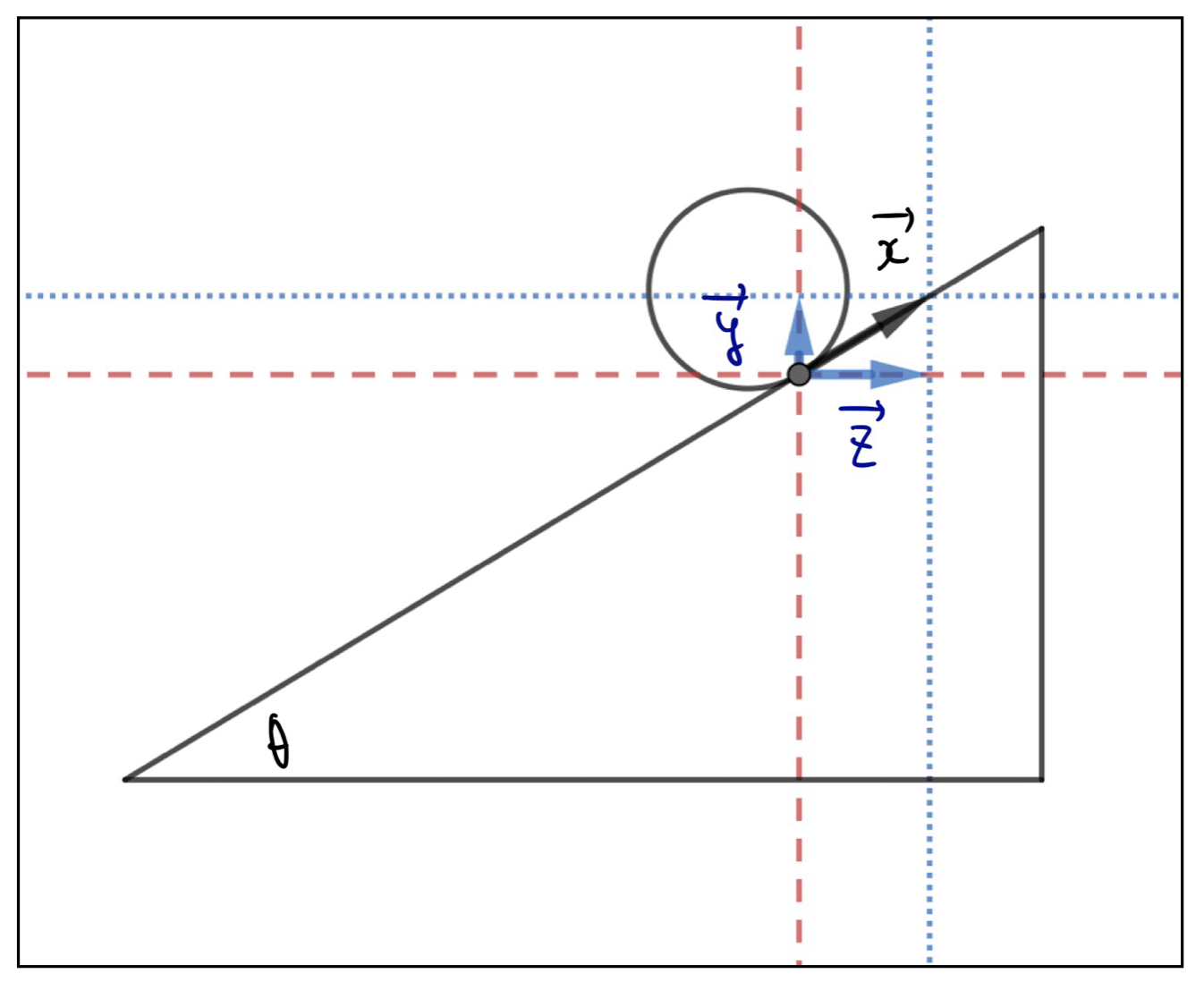
2.
この問題は斜面上の物体にかかる摩擦の分解をイメージした問題です。以下のように分解できます。

\begin{align}
&\vec{x}=\vec{y}+\vec{z}\\
&\left|\vec{y}\right|=\left|\vec{x}\right|\sin\theta\\
&\left|\vec{z}\right|=\left|\vec{x}\right|\cos\theta\\
\end{align}