(※数式が見切れている場合は横スクロールしてください。)
ど頭に一番重要なことを言っておきます。定積分は微小変化、微小面積（もしくは微小体積）を寄せ集めたものというイメージを頭に植え付けてください。
このイメージが物理の勉強において、一番重要な考え方の１つです。
では早速、例として以下のようなものを考えてみよう。
例
次の定積分を計算せよ。
\int^2_1(2x+3)dx
\end{align}
この計算自体は前の節で扱ったものと同じレベルですから、すぐに計算できますよね。以下のようになります。
&\int^2_1(2x+3)dx=\left[x^2+3x\right]^2_1\\
=&(2^2+3\cdot2)-(1^2+3\cdot1)=6
\end{align}
ここに図形的なイメージを合わせていくのが、今回の節のメイントピックです。以下の図をご覧ください。
この図の中にある台形は、\(y=2x+3\)、\(x\)軸、\(x=1\)、\(x=2\)で囲まれた部分です。この面積はすぐに計算できて\(6\)となります。
先程の積分の計算の結果と、この台形の面積の計算の結果が一致するのはもちろん偶然なんかではありません。
台形の中に以下のような長方形を取って来てみよう。
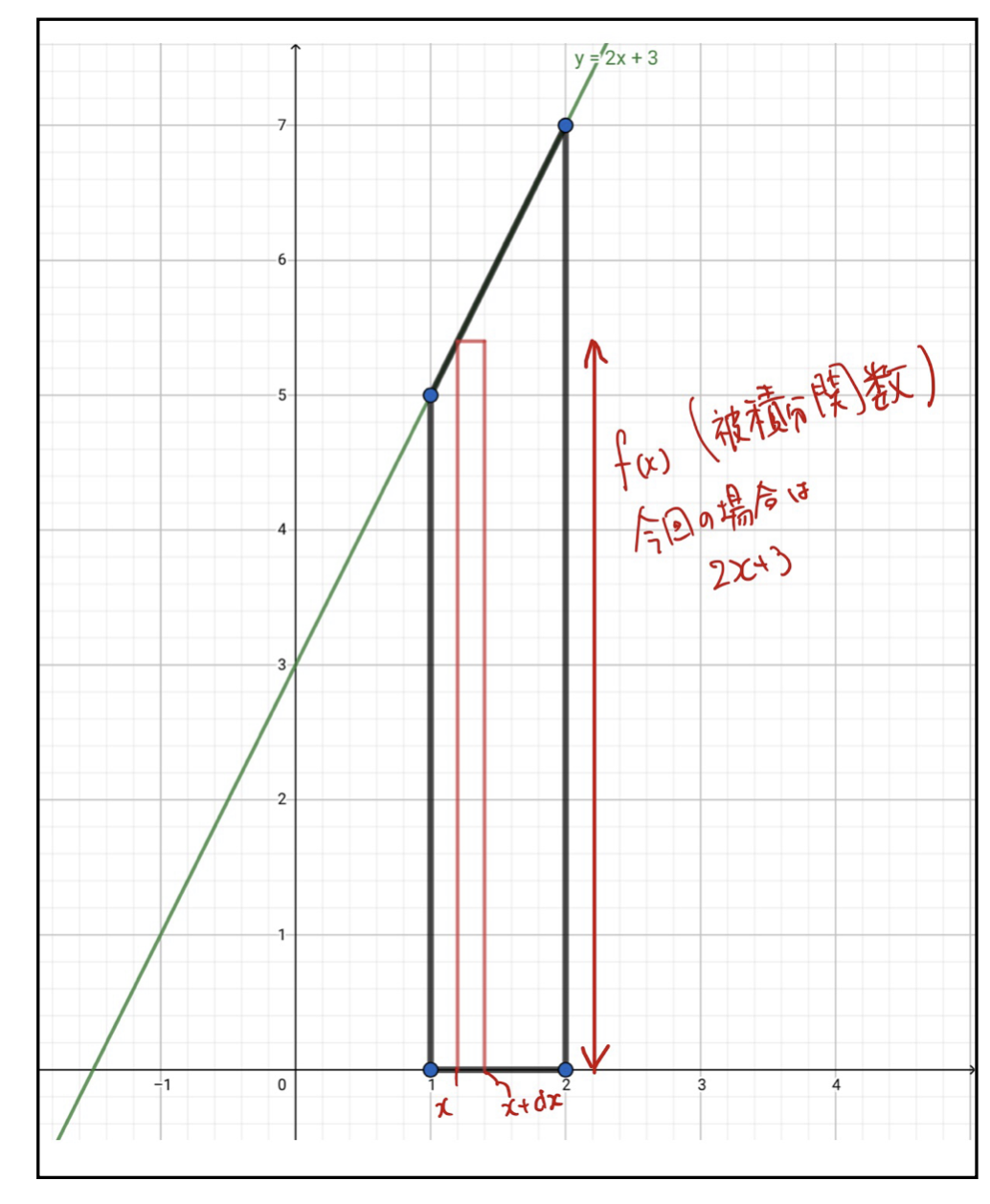
この長方形の横幅は\(dx\)、縦の長さは\(f(x)\)、今回の場合は\((2x+3)\)です。この\(dx\)をものすごーーく小さくして、長方形を並べまくると、ほとんど台形と同じ形が再現できます。
以下の図のように左端から長方形を並べていくイメージですね。（見えます？）
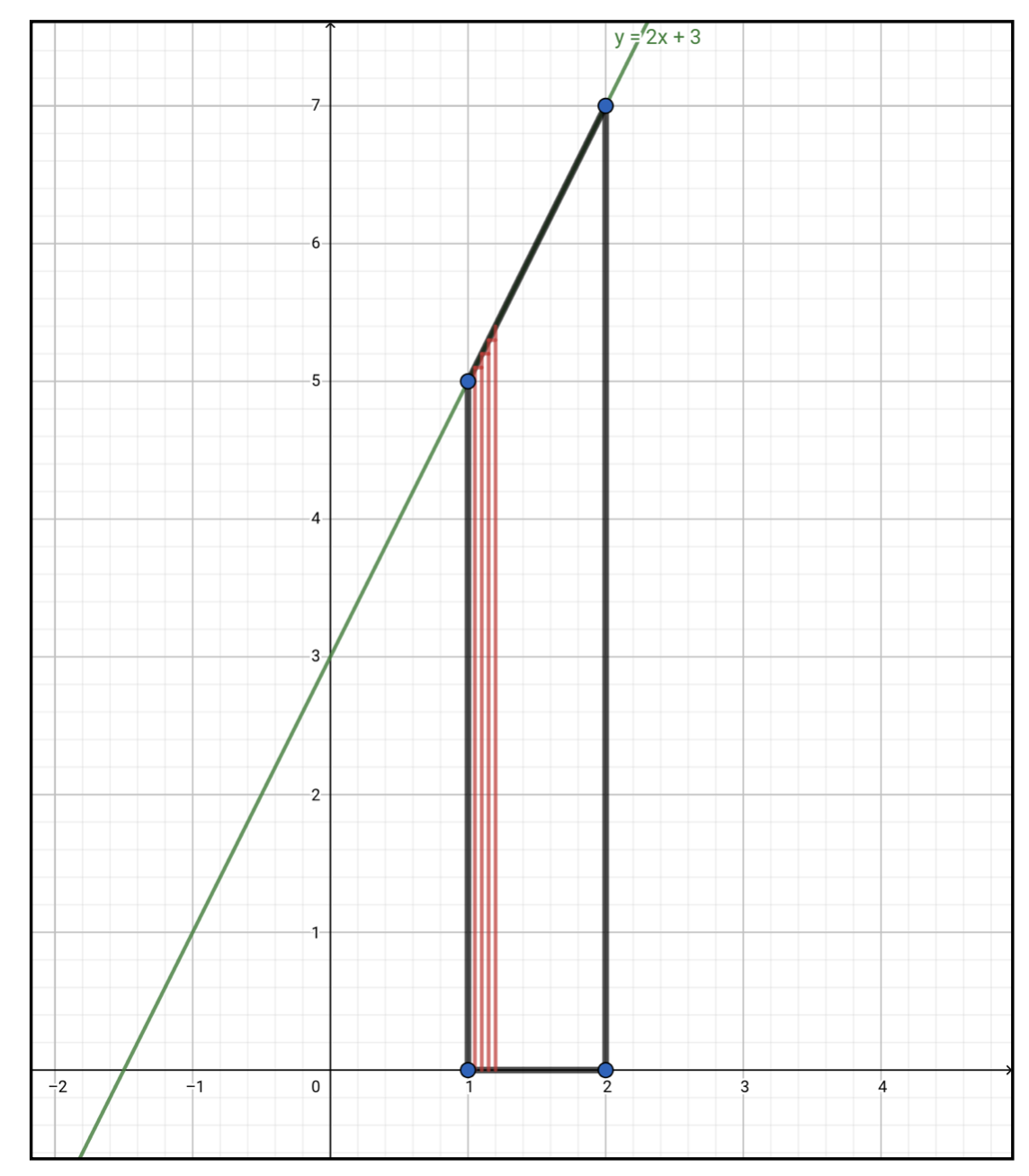
実は定積分のやっていることは、\(dx\)をゼロにする極限での、この長方形（微小面積）を全部足し合わせる和の計算です。
もう一度、定積分の記号を眺めてみましょう。
先程計算した定積分はこんな形をしていました。
\int^2_1(2x+3)dx
\end{align}
まずインテグラルは「足し合わせ」を意味しています。微小長方形を足し合わせるという話を先程しました。その足し合わせ記号だと思ってください。
続いて、積分区間はどこからどこまで足し合わせますか？というものを定義するものです。
被積分関数は微小面積の縦幅を表していて、\(dx\)は微小面積の横幅を表しています。
ここまで解説すると何となく定積分のイメージが湧きましたか？この節の冒頭で言ったように定積分は微小面積の寄せ集めです。
もう少しだけ細かいところまで見ていくことにしましょう。そこで今度は次の定積分を例にとって考えていきます。
例
以下の定積分を計算せよ。
\int^1_{-3}xdx
\end{align}
これも計算自体はものすごく簡単です。
&\int^1_{-3}xdx=\left[\frac{1}{2}x^2\right]^1_{-3}\\
=&\frac{1}{2}\cdot1^2-\frac{1}{2}(-3)^2=-4
\end{align}
微小面積の寄せ集めなのに、なんで結果としてマイナスの値が出るのだろうと不思議に思うかもしれませんね。先程と同様に図形で意味を考えることにします。
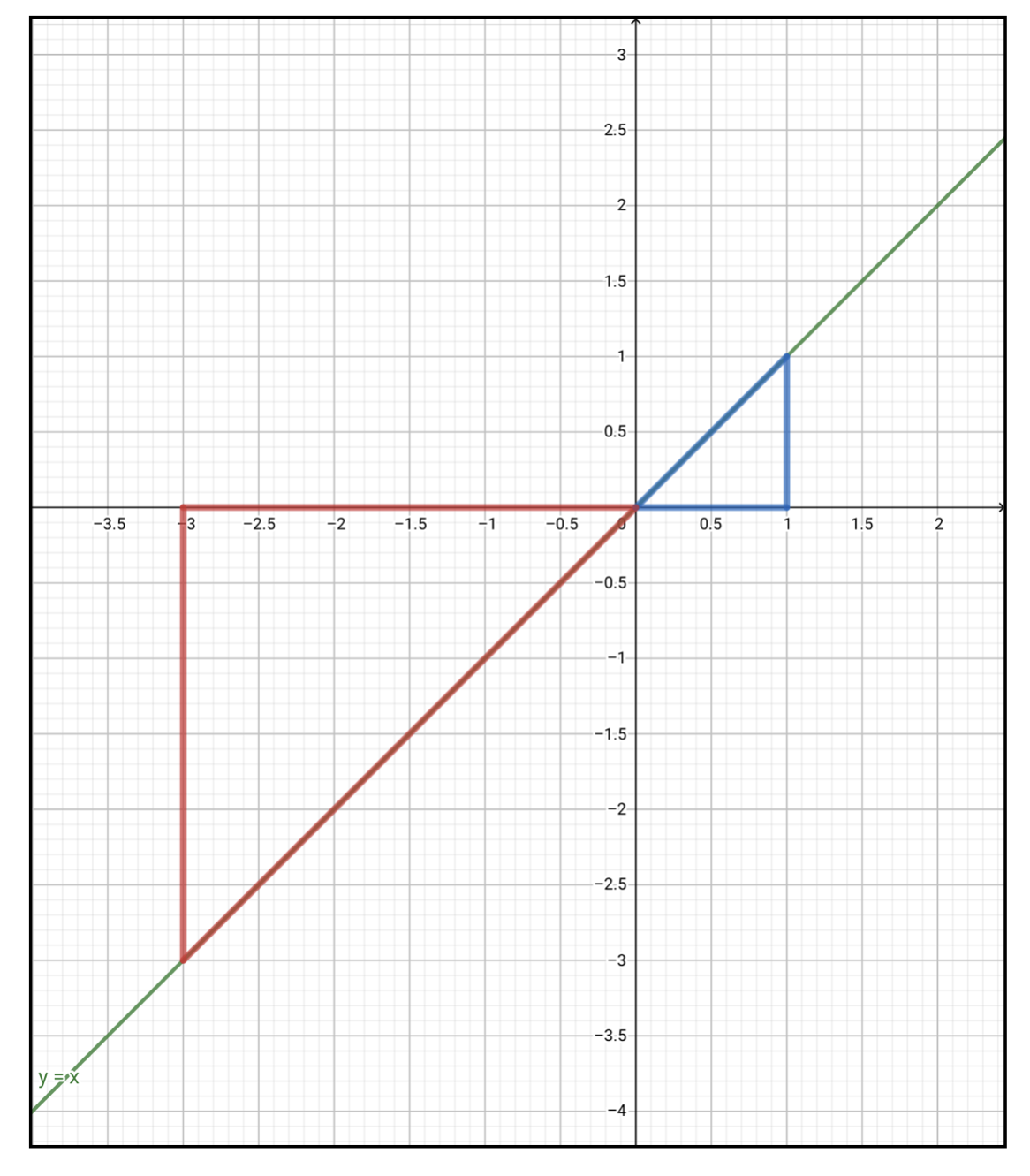
先程、被積分関数は微小面積の高さを表すと書きました。
それに従うと、\(x\)が\(-3\)から\(0\)の間では被積分関数はマイナスの値を返すので、これはすなわち高さとしてマイナスの値を採用していることになりますよね。図の左側（赤い三角形）は高さをマイナスで計算していることになるので、面積としてもマイナスの値が出てきてしまいます。
被積分関数が、正負で別れる部分で場合分けして以下のようにかくとわかりやすいかもしれませんね。
&\int^1_{-3}xdx=\int^0_{-3}xdx+\int^1_0xdx\\
=&\left[\frac{1}{2}\right]^0_{-3}+\left[\frac{1}{2}x^2\right]^1_0=-\frac{9}{2}+\frac{1}{2}
\end{align}
１つ目の等号のところで、左側の赤い三角形に対応する部分の積分と、右側の青い三角形に対応する部分の積分に分けました。
ちなみに分けるときに自然に以下の公式を使いました。後出し的に書いておきます。
公式
\int^{\beta}_{\alpha}f(x)dx=\int^{\beta}_{\gamma}f(x)dx+\int^{\gamma}_{\alpha}f(x)dx
\end{align}
定積分の記号の意味と図形の意味の対応が理解できていたら当たり前の公式ですよね。
この公式は定積分の積分区間を2つに分割しただけのことだですから。もちろん、3つに分解することも4つに分解することも可能で、積分区間の上添字と下添字を合わせるように分割していけばいいだけです。
より一般的にグラフ中のとある部分に着目してその面積を正確に出したい場合にはどうすればよいでしょうか。
先ほどの例で言うと、赤三角と青三角を両方とも正の値で計算し、合計の面積を出したいときにはどうしたらいいか、ということです。
マイナスの高さが出てくる場合は、それを避けない限りは真の意味で面積を計算することはできません。が、逆に考えると高さがマイナスになるのが、問題であったわけなので、それを避ければいいだけです。
先程の例は、\(y=x\)と\(y=0\)のどちらがグラフの上側に来るかという観点で場合わけしました。より一般には面積を求めたい場合には、
（大きいもの）ー（小さいもの）
\end{align}
を被積分関数として採用すれば、面積の計算は間違えないわけですね。
先の例で、「赤三角と青三角の面積の合計を計算せよ」と言われたら、以下のように考えろということです。
&\int^0_{-3}(0-x)dx+\int^1_0(x-0)dx\\
=&-\left[\frac{1}{2}x^2\right]^0_{-3}+\left[\frac{1}{2}x^2\right]^1_0=\frac{9}{2}+\frac{1}{2}
\end{align}
初項の被積分関数の部分で\(x\)と\(0\)の大小を考え、大きいものマイナス小さいものを被積分関数として採用しています。
ここまで行けば、マキノさんは微分積分も簡単なことなら分かりますと言い張っていただいて構いません。微分と積分だけを学ぼうと思うと意外とこれくらいのページ数でも勉強できてしまうものなんです。
最後に以下の問題を解いて、面積の出し方を覚えてもらいましょう。
問題
以下の赤線で囲まれた部分の面積を計算せよ。
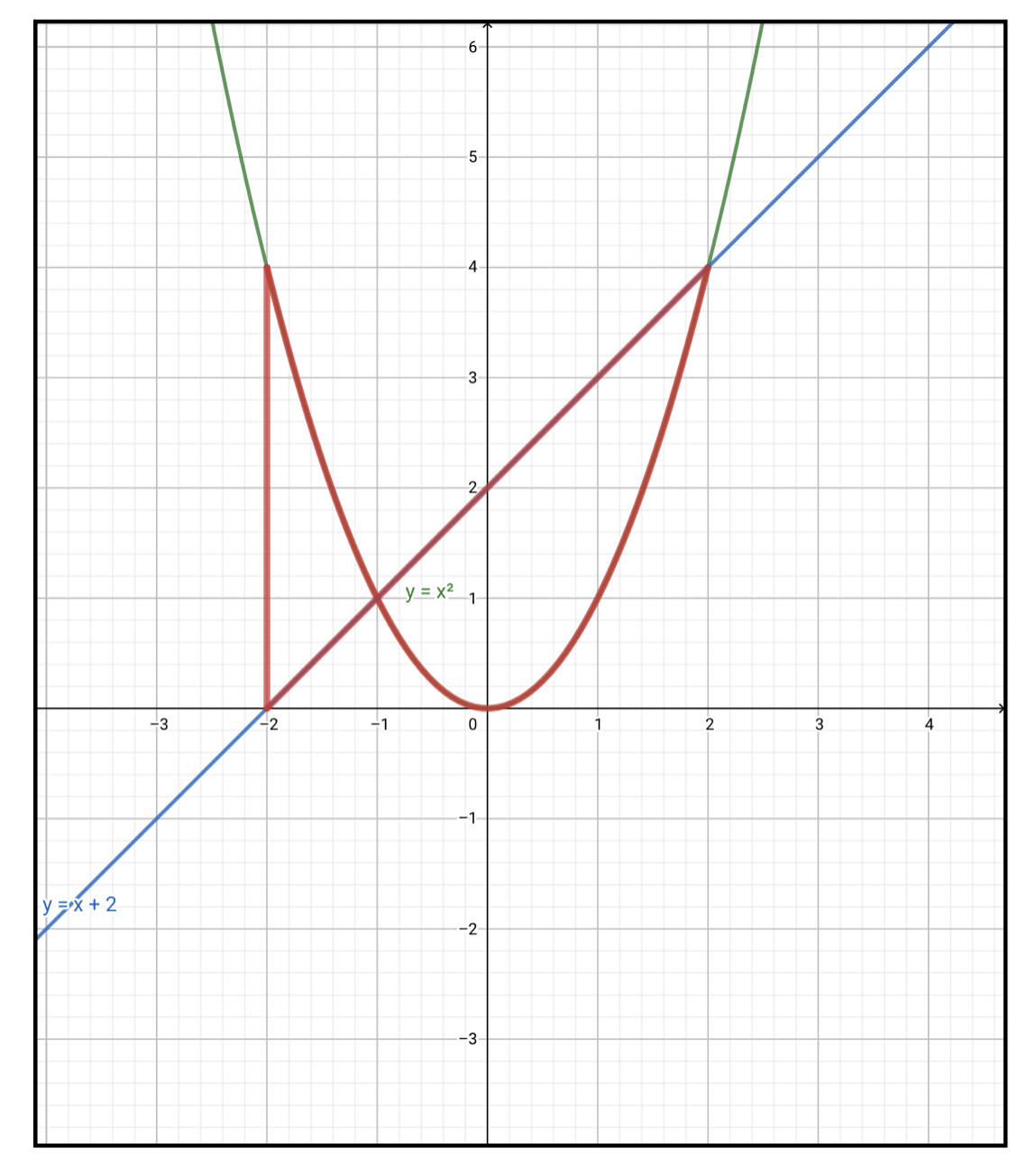
解答
まず積分をする前に、2つのグラフの交点のx座標を求めなければならないですがそれは中学生レベルの数学なので省略しますね。
図にも小さく書いたのですが、与えられた放物線と直線の式は以下のとおりです。
\begin{cases}
y=x^2\\
y=x+2
\end{cases}
\end{align}
交点を求めるには両グラフの式を連立させれば良いです。交点のx座標は
x=2,\quad-1
\end{align}
ということがわかります。図から各積分範囲でグラフの大小は明らかなので、求める面積は以下の積分となりますね。
\int^{-1}_{-2}(x^2-x-2)dx+\int^2_{-1}(-x^2+x+2)dx=\frac{19}{3}
\end{align}
計算部分は省略しましたが、計算できましたか？出来なければ、前の章に戻るか、問題集の方で少し問題に慣れてからもう一度挑戦してみてください。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」
東大理系攻略法を
解説したPDF販売中！
中高一貫校に行かなくても、塾に行かなくても、独学で受かるための勉強法を完全解説！
全科目の参考書
全参考書の使い方
受験までの勉強スケジュール
が全てわかります！
今だけ！100様限定60%OFF！
さらに24時間以内なら返金保証つき！
無料サンプル公開！
