(※数式が見切れている場合は横スクロールしてください。)
前の節までで、力積と運動量という概念に少しは慣れていただけましたかね。先程の節では、注目するのは1つの物体で、衝突のお相手は床、物理では環境とかいう言い方をするものでした。今度は2物体に着目して、その衝突などなどについて議論していきましょう。
まずは以下の設定で2物体間の運動量の変化を見ていくことにします。
例
質点Mと質点mの運動を考える。
質点Mは時刻\(t_1\)に速度\(\vec{V}(t_1)\)を、質点mは同じ時刻に速度\(\vec{v}(t_1)\)であるとする。
次に観測を行った時刻\(t_2\)において、Mの速度は\(\vec{V}(t_2)\)に、mの速度は\(\vec{v}(t_2)\)に変化していた。
この２つの時刻の間に働く力は2物体間の相互作用だけだとする。
この相互作用というのはどんなものでも構いません。例えば、Mとmは接触をしてその間に力を及ぼしていたかもしれないですし、Mとmが磁気を帯びていて、引っ張りあったり反発しあったりしていたかもしれません。
ここで重要なのは、2物体の間だけの相互作用以外に力が働いていなかったということです。重力とかも含めて今の状況では他の力は考えません。
では具体的に話を進めていきます。
この2つの時刻の間の任意の時刻においてMはmへ力\(\vec{F}(t)\)を与えていたとすると、作用反作用の法則から、mはMへ対して力\(-\vec{F}(t)\)を与えていたことになります。
運動量の変化によって力積が与えられるので、以下のような式が立てられますね。
&M\vec{V}(t_2)-M\vec{V}(t_1)=\int^{t_2}_{t_1}\vec{F}(t)dt\\
&m\vec{v}(t_2)-m\vec{v}(t_1)=-\int^{t_2}_{t_1}\vec{F}(t)dt
\end{align}
上の式がMに対する運動量の変化を記述した式で、下の式がmに対する運動量の変化を記述した式です。
右辺は作用反作用の法則から、符号が違うものが並んでいますね。そこで、両者の左辺同士、右辺同士を足し合わせると（辺々足すという表現を使うことがあります。）、
&M\vec{V}(t_2)-M\vec{V}(t_1)+m\vec{v}(t_2)-m\vec{v}(t_1)=\vec{0}\\
\Longleftrightarrow
&M\vec{V}(t_1)+m\vec{v}(t_1)=M\vec{V}(t_2)+m\vec{v}(t_2)
\end{align}
となります。この２つ目の式をよく見ると、時刻\(t_1\)のときの2つの質点の運動量の和と、時刻\(t_2\)のときの運動量の和が等しいことが分かりますね。
この事実を公式としてまとめておきます。
公式
2つの物体の間に相互作用が働いていて、それ以外の外部からの力(外力)が働いていないときには、任意の時刻間で２つの運動量の総和は保存する。
&M\vec{V}(t_1)+m\vec{v}(t_1)=M\vec{V}(t_2)+m\vec{v}(t_2)\\
\Longleftrightarrow
&M\vec{V}(t)+m\vec{v}(t)=const.
\end{align}
この公式のことを運動量保存則という。
さて、この公式を導く上で大事だったことをおさらいしておきますね。
まず前提条件として、相互作用以外に外部から力が働いていないことが重要でした。例えば、2つの時刻の間に指で質点を弾き飛ばすというような余計な力積を与えてしまうともちろんダメなわけです。それは外力ですからね。
相互作用は作用反作用の法則から反対向きのベクトルになるので（そしてそれ以外の力がないので）、運動量の変化を記述した式を足し合わせると、保存則が導けるわけです。
さて、この運動量保存の法則はベクトルによって表現された方程式ですが少しだけ注意すべきことがあります。
運動方程式を解くときに、成分ごとに計算をすることがありましたよね。この運動量保存則もある一方向では保存則が成立しているけど、違う方向では成立していないというようなことがあります。もちろん各方向全てで成立しているようなこともあります。
重要なのは、相互作用以外の力が働いていない方向では、その成分に着目すると運動量の保存則が成立しているという点です。外力が働いている方向には保存してなくても、働いていない方向には保存していたりするというわけですね。
慣れるためにまずは衝突の問題を解いてもらうことにしますね。
問題
以下の図のように質点Mと質点mが直角に交わる方向から、それぞれ速さ\(V\)と速さ\(v\)で近づいてきているとする。
そして、衝突後、質点Mは角度\(\theta\)で表される方向に速さ\(V’\)で進んでいることを観測した。図参照。
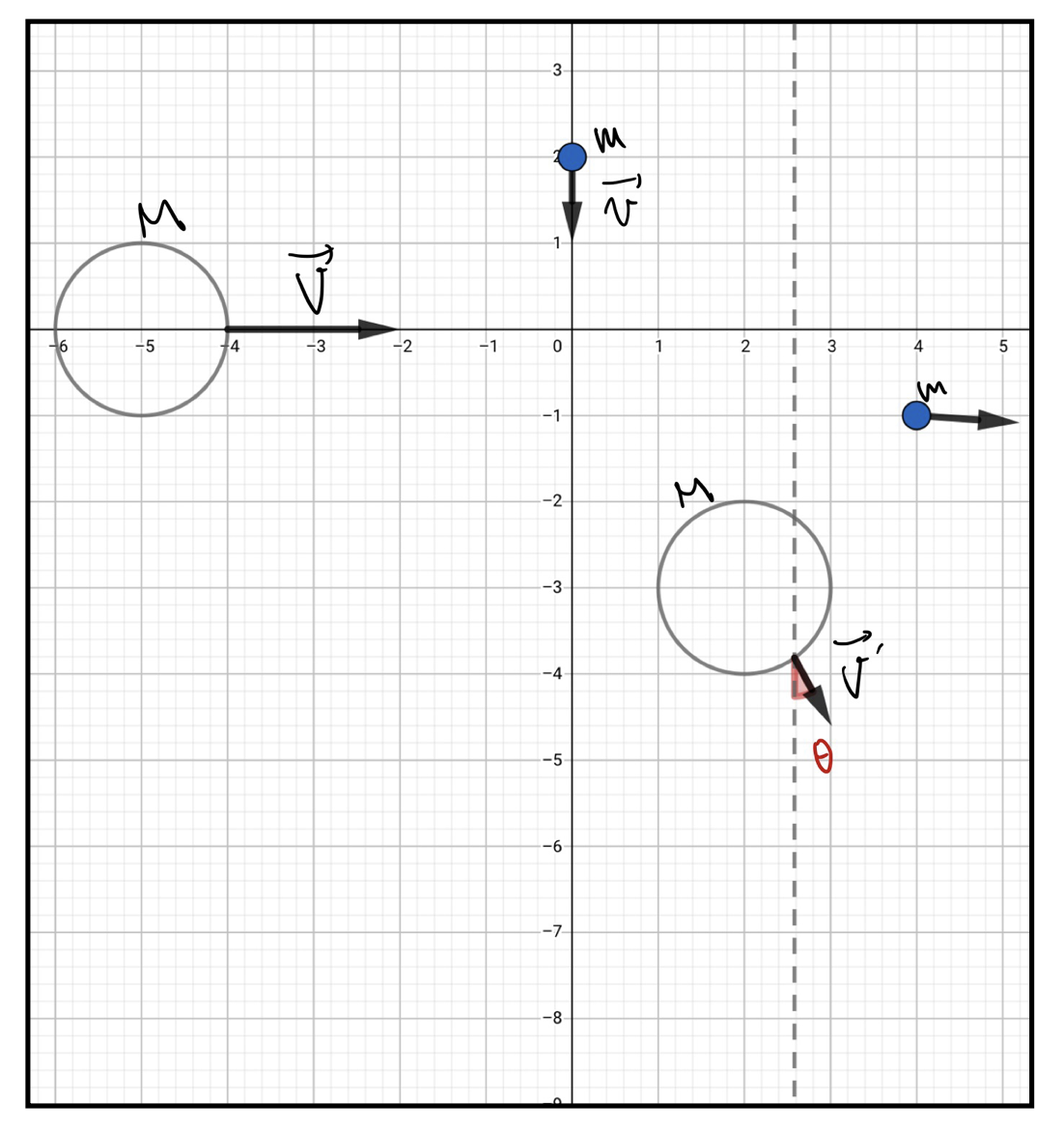
このとき質点mの衝突後の速度を求めよ。
ただし、衝突の短い時間だけ両者に相互作用が働いており、それ以外の力は衝突前後も含めてかかっていないとする。
解答
衝突前にMが進んでいる方向をx成分で、mの進んでいる方向を\(y\)成分で表現することにしましょう。
そのとき、衝突後のMの速度は以下のベクトルで表現できます。
\vec{V’}=\begin{pmatrix}V’\sin\theta\\V’\cos\theta\end{pmatrix}
\end{align}
外力が働いていないので、運動量保存の公式が使えます。
&M\vec{V}+m\vec{v}=M\vec{V’}+m\vec{v’}\\
\Longleftrightarrow
&M\begin{pmatrix}V\\0\end{pmatrix}+m\begin{pmatrix}0\\v\end{pmatrix}=M\begin{pmatrix}V’\sin\theta\\V’\cos\theta\end{pmatrix}+m\vec{v’}\\
\Longleftrightarrow
&\vec{v’}=\begin{pmatrix}\frac{M}{m}(V-V’\sin\theta)\\v-\frac{M}{m}V’\cos\theta\end{pmatrix}
\end{align}
問題として、衝突を手始めに取り扱いましたが、合体や分裂についても同じように議論ができます。以下の問題で見ていただきましょう。
問題
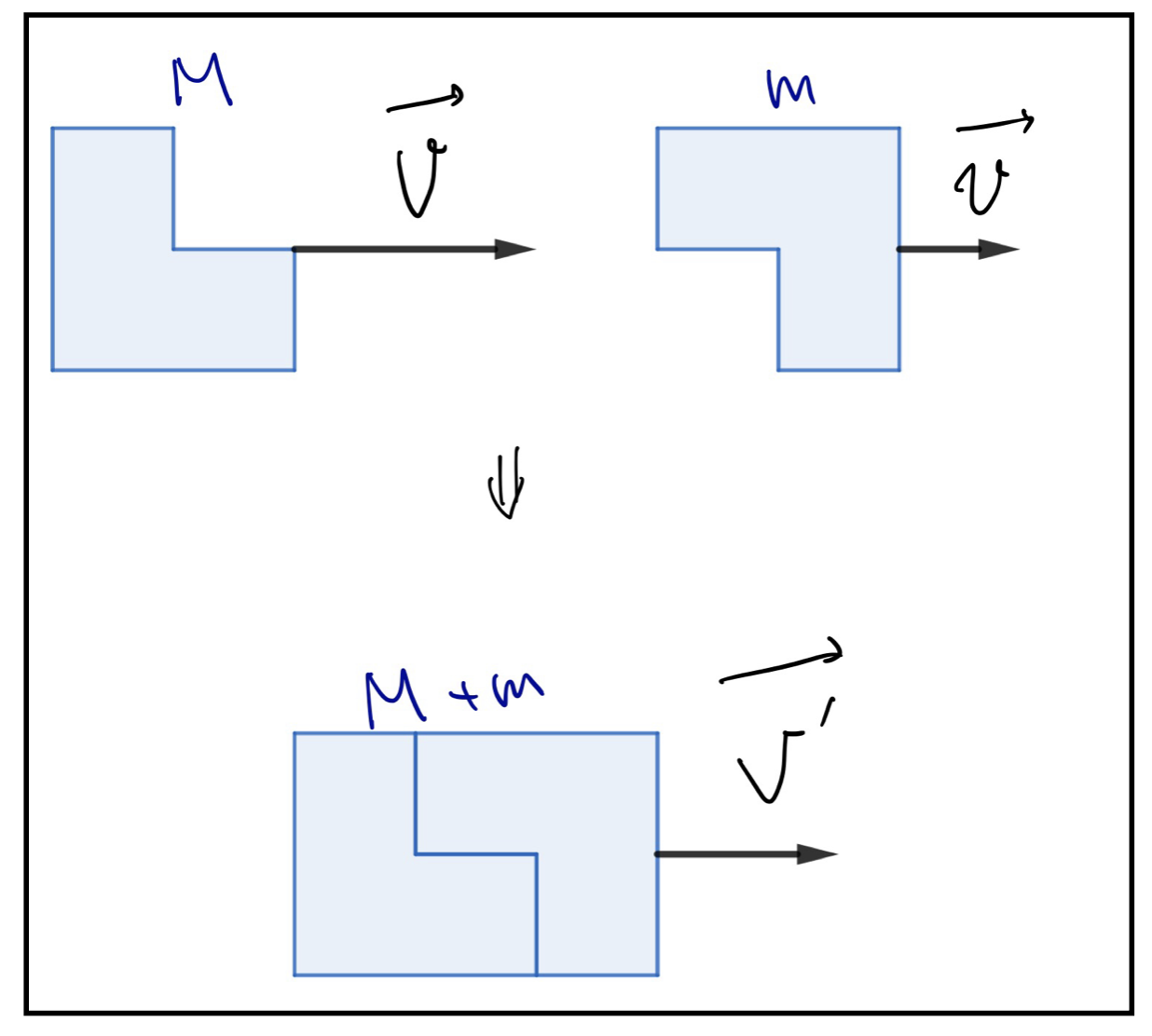
以下の図のように衝突前に質量\(M\)だったものと、質量\(m\)だったものが一直線上に並んで、同じ向きに速さ\(V\)と\(v\)で進んでいるとする。
ある時刻で物体Mとmは合体し、その後１つの物体として、運動を始めた。
合体後の物体の速さを求めよ。ただし、合体に必要な2物体の間の相互作用以外には力は働いていないものとする。
解答
やはりここでも外力は働いていないので運動量が合体前後で保存します。今回は一直線上の運動を考えるので、文字の正負さえ意識すれば、ベクトルで考えずとも大丈夫です。
MV+mv=(M+m)V’\quad\Longleftrightarrow\quad V’=\frac{MV+mv}{M+m}
\end{align}
分裂に関しては先ほどの合体の問題の順序が逆になったものと考えればよいです。つまり運動量保存の式において、左辺が合体前、右辺が合体後、と考えていたものを右辺が分裂前、左辺が分裂後と考えれば、同様の議論ができることがわかります。
最後にこれまでに習った内容をここで習った運動量の概念と合わせて総合的な例に挑戦して、さらにここで習った概念に慣れておきましょう。
例
図のように質点mと質点Mが初速度\(\vec{v_0}\)と\(\vec{V_0}\)を持っているとする。それらの向きは互いに真逆を向いているので、あるタイミングで正面から衝突し、その後、mとMはそれぞれ逆向きに運動しだした。その速度は\(\vec{v_1}\)と\(\vec{V_1}\)であった。
この衝突のはね返り係数を求めよ。（ただし外力は一切かかっていないとする。）
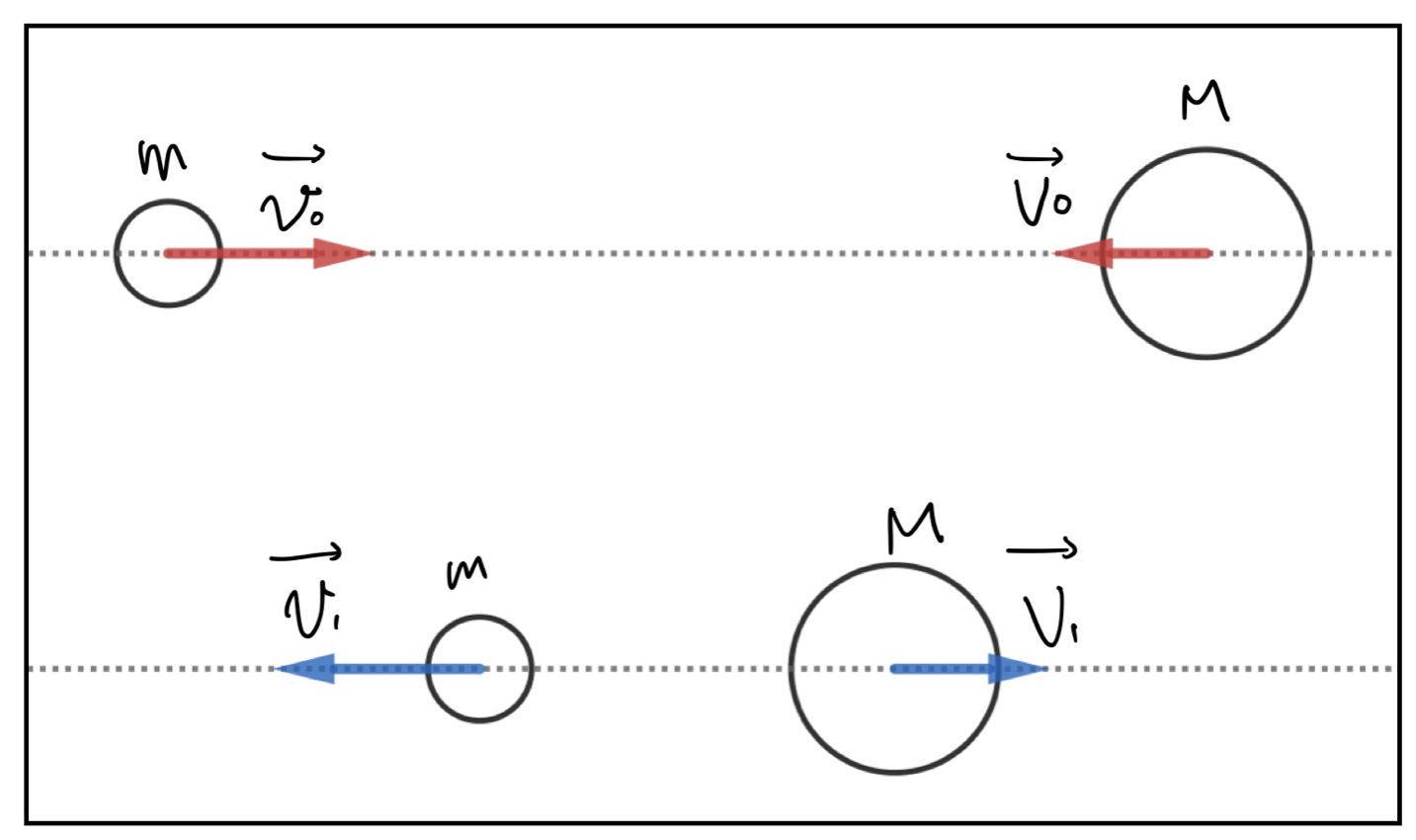
今回の例に関しては「相対速度」「運動量」「はね返り係数」の考え方が理解できていれば理解できるはずです。今回の例が難しく感じられるようなら、このキーワードに該当する部分をもう一度読み直してみてくださいね。
はね返り係数は床に何かが衝突する現象をもとにこのテキストでは解説しましたから、今回与えられた例をその設定に持ち込めるように読み替える必要があります。
まず、この例の設定として与えられているのは、質点を外から眺めた人から見た速度ベクトルです。これをMが静止しているように見える人からの目線に変えてやります。
要するに、Mの上に乗っている人からこの現象をみるとどのように見えるか考えればいいわけです。
その視点からこの現象を見ると、Mは静止しているわけですから、壁に向かって質点mが衝突してきてはね返るのと全く同じ状況になりますね。
ただし、この時に重要なのは、質点Mの静止系から見るときに質点mの運動はどのように見えているのかということです。もっと単純に言うと、議論を進めるために相対速度を使えということですね。
さて、相対速度の復習ですよ。質点Mから見たときに、質点mはどういう速度で見えているでしょうか。
衝突前は\(\vec{v_0}-\vec{V_0}\)と見えていて、衝突後には\(\vec{v_1}-\vec{V_1}\)と見えているはずですね。「相手マイナス自分」としたものが、相対速度になるのでした。思い出してください。
はね返り定数は、「元の速さ」×「はね返り定数」＝「後の速さ」という風にしていたので、ベクトルではなくて、ベクトルの大きさを使って考えた方がいいですね。
今回求めたいはね返り定数を\(e\)とすると、
\left|\vec{v_0}-\vec{V_0}\right|\times e =\left|\vec{v_1}-\vec{V_1}\right|
\end{align}
から、
e=\frac{\left|\vec{v_1}-\vec{V_1}\right|}{\left|\vec{v_0}-\vec{V_0}\right|}
\end{align}
と求められます。
この章では、運動方程式を出発点として、全体を時間積分することによって運動量の変化を議論しました。そして、その例として、1つの物体と環境（床）との衝突を見てみたり、2物体の衝突や合体の運動量の保存則を作用反作用の法則を使うことで導きました。次の内容としては、運動方程式を時間ではなく、空間の成分で積分するとどうなるのかというあたりを議論することになります。エネルギーという概念を新たに導入し、議論を進める様子をご覧いただきたいのですが、
その前に一度、数学の準備を挟むことにしますね。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」
東大理系攻略法を
解説したPDF販売中！
中高一貫校に行かなくても、塾に行かなくても、独学で受かるための勉強法を完全解説！
全科目の参考書
全参考書の使い方
受験までの勉強スケジュール
が全てわかります！
今だけ！100様限定60%OFF！
さらに24時間以内なら返金保証つき！
無料サンプル公開！
