(※数式が見切れている場合は横スクロールしてください。)
図形の方程式に少し操作を加える話です。
ここまでに中学数学を含めて図形の方程式は以下のようなものを習っています。
直線、放物線、円、だ円、双曲線
それぞれ式の形を書くことができますかね。
怪しいなら復習してから、この節の続きを進めてください。
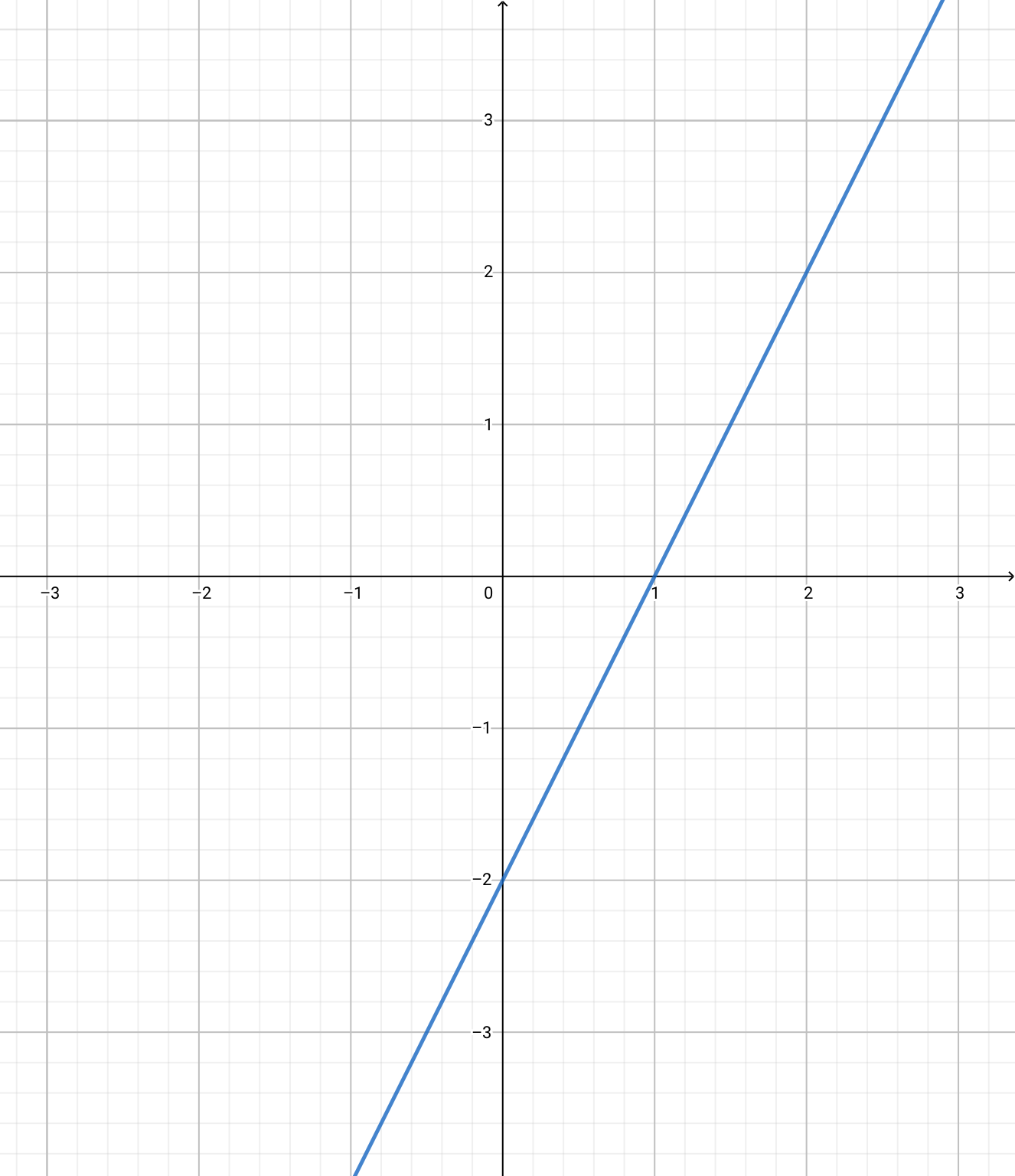
まず例として\(y=2x\)という直線の平行移動を扱ってみましょう。
全く同じ意味を表しますが、少し移項をして以下の形を標準的なものとして扱います。
2x-y=0
\end{align}
特にここでは、この左辺を\(f(x,y)\)という2変数関数としたうえで扱います。
2変数関数はこれまでにほとんど見たことがないかもしれませんが、それほど難しいものではありません。
先ほど挙げた図形の方程式は全て
f(x,y)=0
\end{align}
という形にできますから、この形で扱う方がより一般的に議論できるというわけです。
まず、
f(x-1,y)=0
\end{align}
という方程式がどのような図形を表すか考えてみます。
\(f\)という関数の定義を思い出せば中学生でも以下のように計算を進めることは簡単なはずです。
&f(x-1,y)=0\\
\Longleftrightarrow
&2(x-1)-y=0\\
\Longleftrightarrow
&y=2x-2
\end{align}
最終結果は中学生レベルの数学で習っているはずですから、すぐにグラフを書くことが出来ますね。
以下の図のような直線を表します。
これはもともとのグラフと一緒に表示してみると平行移動の関係にあることがわかります。
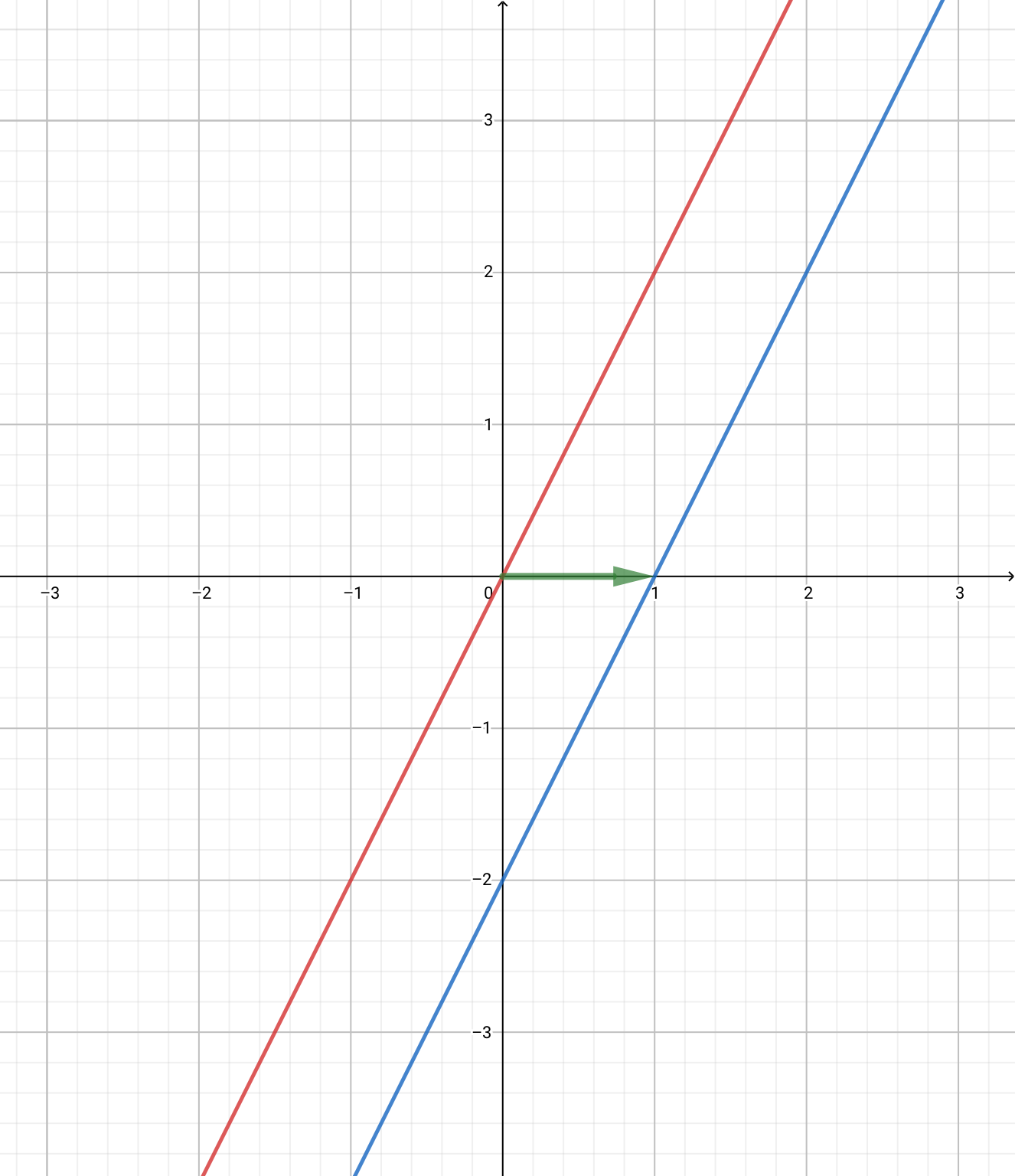
矢印が示しているのは\(f(x,y)=0\)のグラフを\(x\)軸方向に\(+1\)だけ平行移動させたものが\(f(x-1,y)=0\)のグラフであるということです。
より一般に\(f(x,y)=0\)を\(x\)軸方向に\(+a\)だけ平行移動させたものは\(f(x-a,y)=0\)となります。
もちろん\(y\)軸の方向に平行移動させるときも同じように考えればいいので、それらをまとめると以下の公式となります。
公式
f(x,y)=0
\end{align}
のグラフを\(x\)軸方向に\(+a\)、\(y\)軸方向に\(+b\)だけ平行移動させたものは
f(x-a,y-b)=0
\end{align}
となる。
非常に簡単ですよね。あとは慣れの問題ですから、問題を解いてみましょう。
問題
以下のグラフをかけ。
1.
y=2(x+3)^2-2
\end{align}
2.
(x-3)^2+(y+1)^2=1
\end{align}
3.
\frac{(x+1)^2}{16}+\frac{(y-2)^2}{9}=1
\end{align}
4.
-\frac{(x+1)^2}{16}+\frac{(y-2)^2}{9}=1
\end{align}
5.
y=\frac{6}{x-2}+1
\end{align}
問題
1.
この問題は\(y=2x^2\)を\((-3,-2)\)だけ平行移動させればいいです。
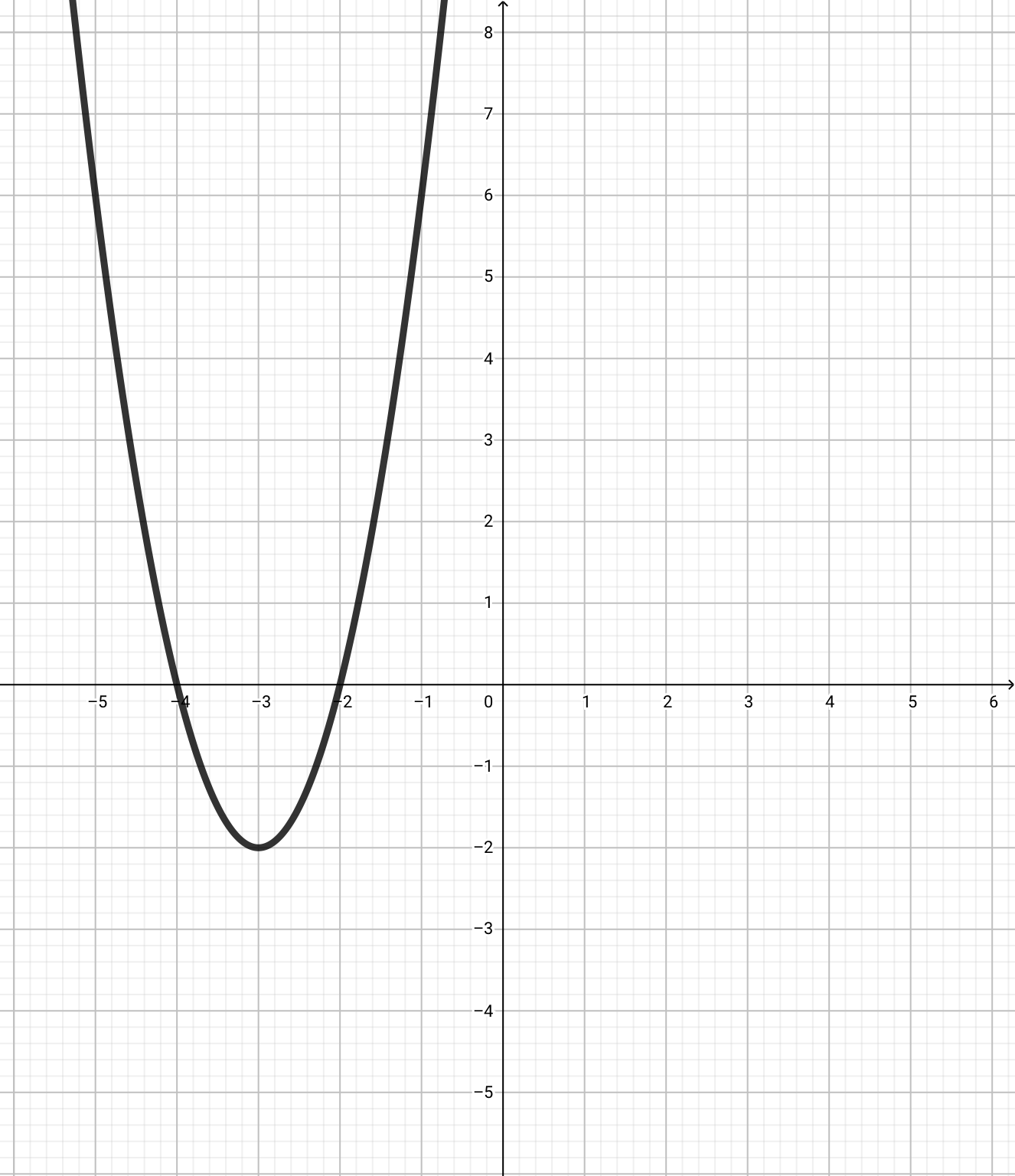
もちろん頂点はずれますけど、放物線の傾き自体は平行移動する前のものと変わりません。
2.
次は\(x^2+y^2=1\)を\((+3,-1)\)だけ平行移動させればいいです。
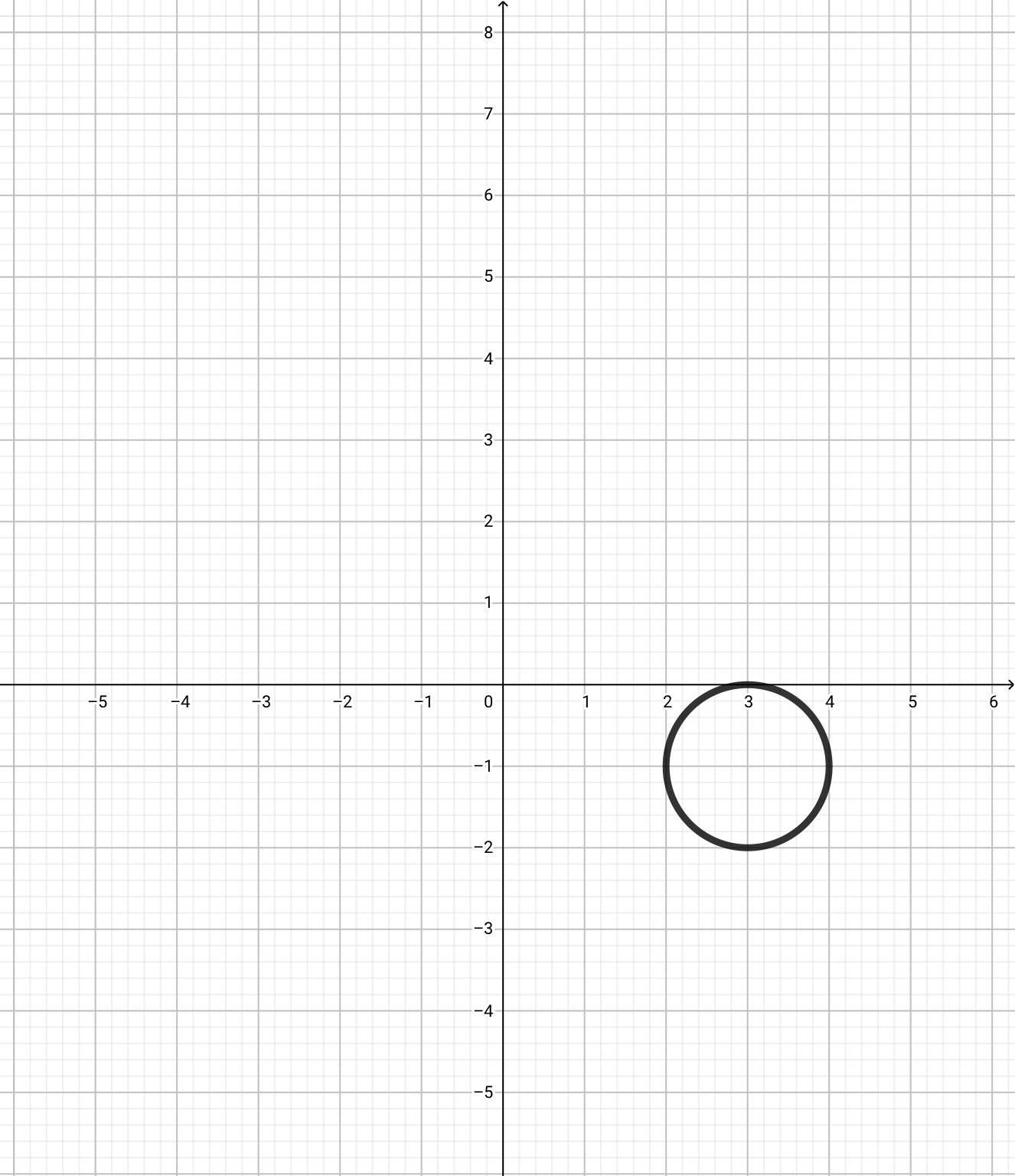
中心の位置は変わりますが、半径は変わりません。
3.
次は\(\frac{x^2}{16}+\frac{y^2}{9}=1\)を\((-1,+2)\)だけ平行移動させればいいです。
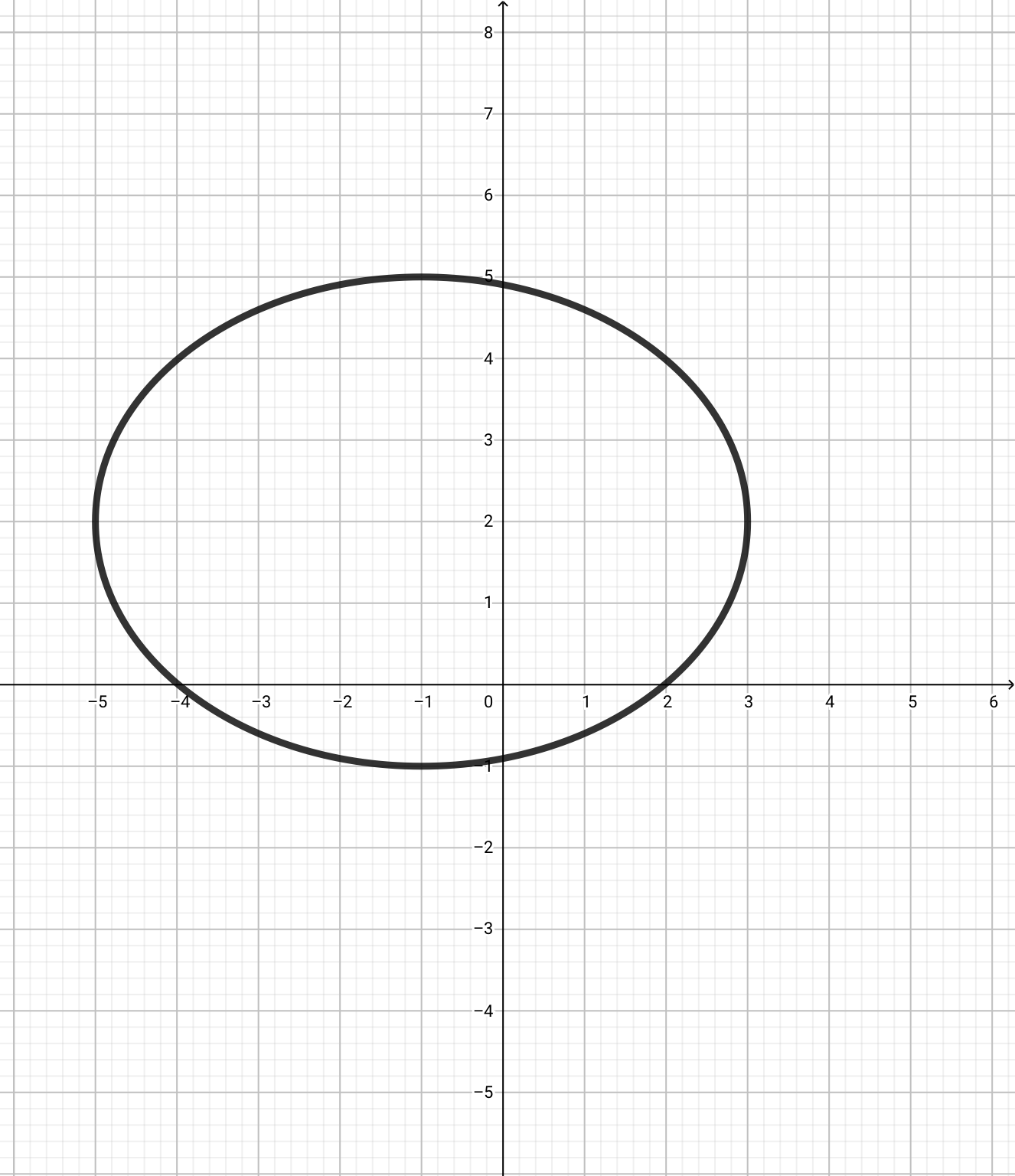
焦点の位置は変わりますが、短半径、長半径といった形を表すものは変わりません。
4.
次は\(-\frac{x^2}{16}+\frac{y^2}{9}=1\)を\((-1,+2)\)だけ平行移動させればいいです。
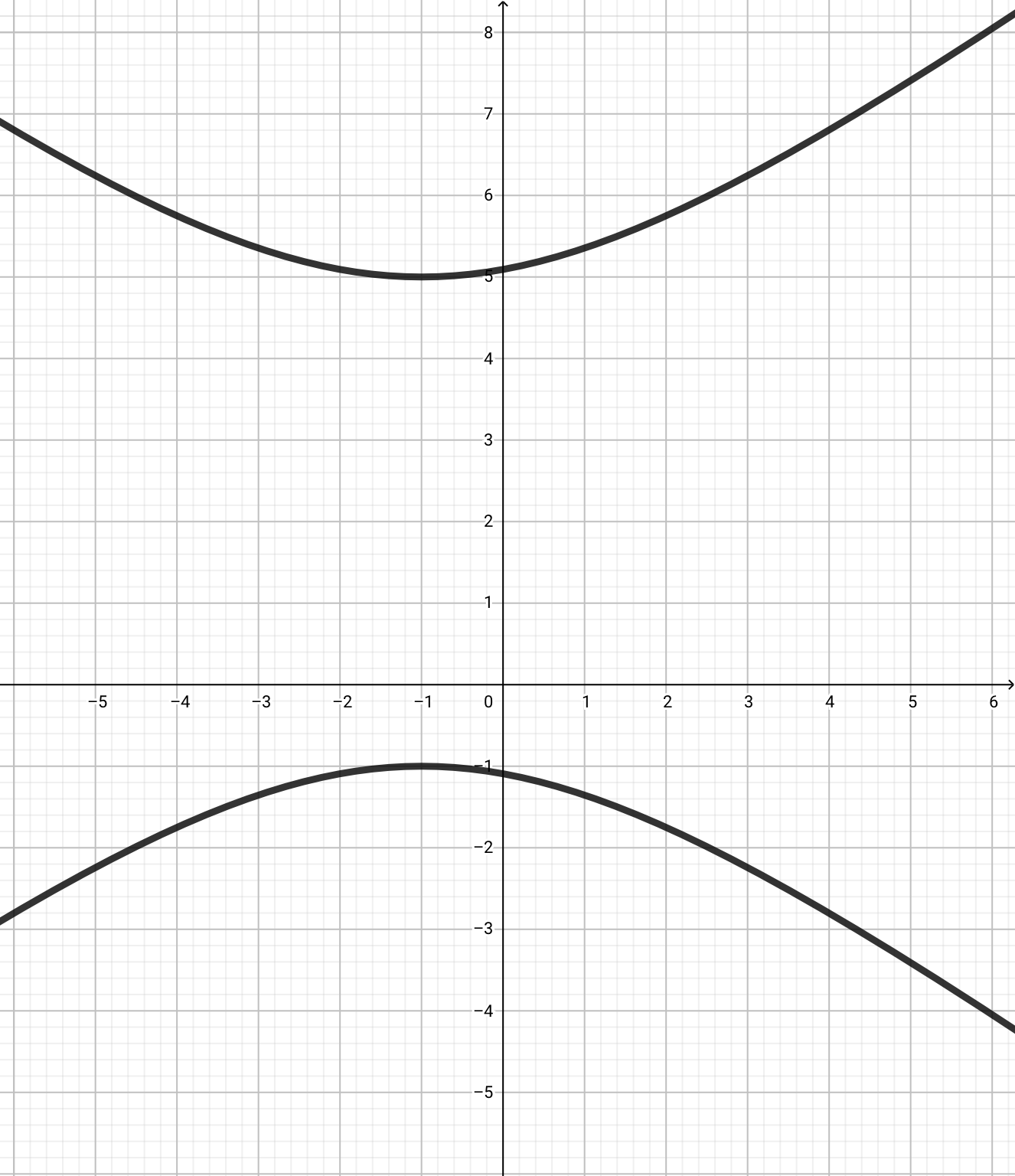
焦点は動きますが、開き具合は変わりません。
5.
次は\(y=\frac{6}{x}\)を\((+2,+1)\)だけ平行移動させればいいです。
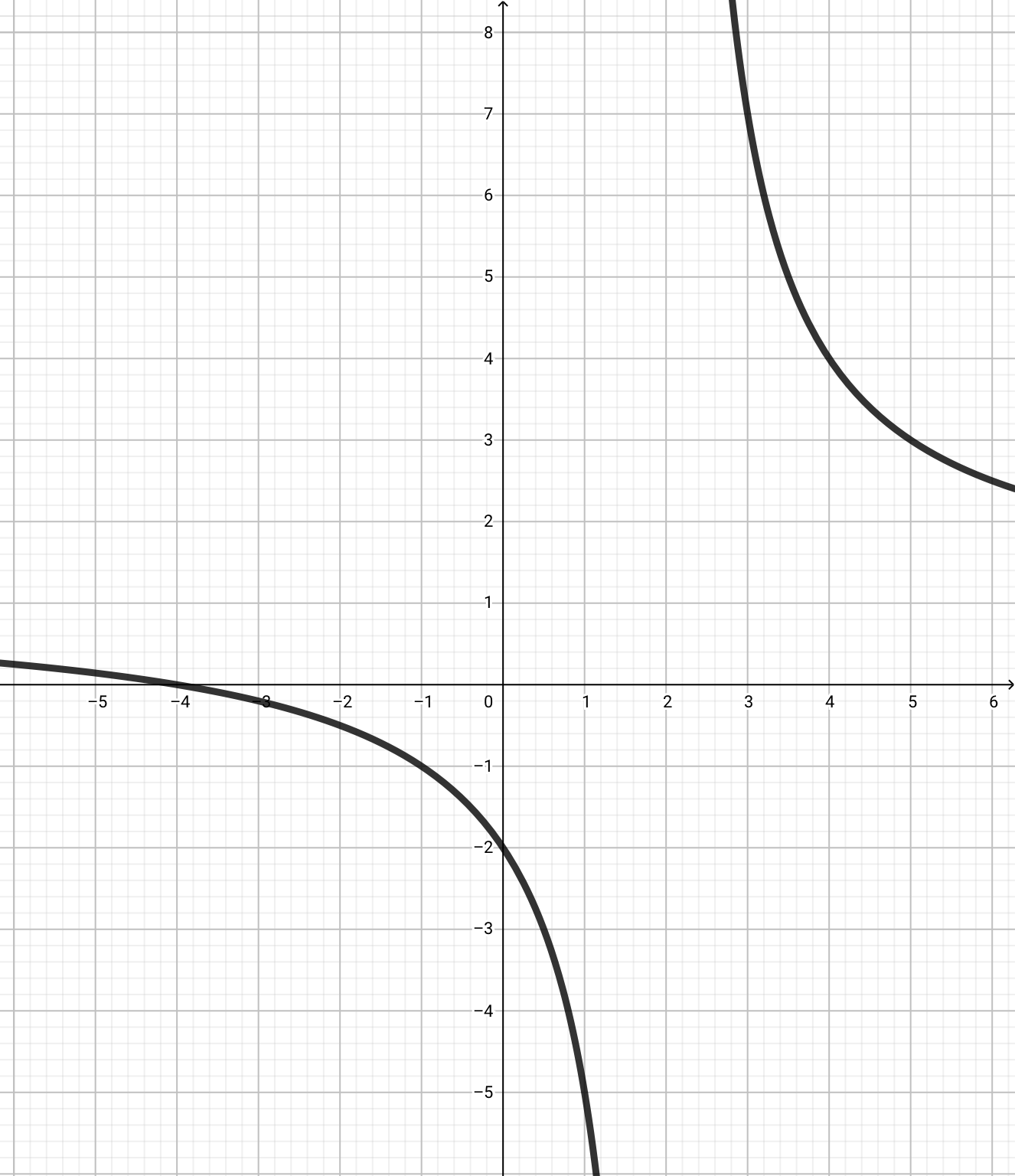
反比例のグラフも中学範囲ですけど、忘れていたら、復習しておいてください。
最後に拡大と縮小を扱います。
今の段階では基本的に円とだ円の関係が分かっていれば大丈夫なので、それだけ扱うことにします。
例として\(x^2+y^2=9\)という円と、\(x^2+y^2/9=1\)というだ円を比べることとしましょう。
グラフを描くと以下のような形になります。
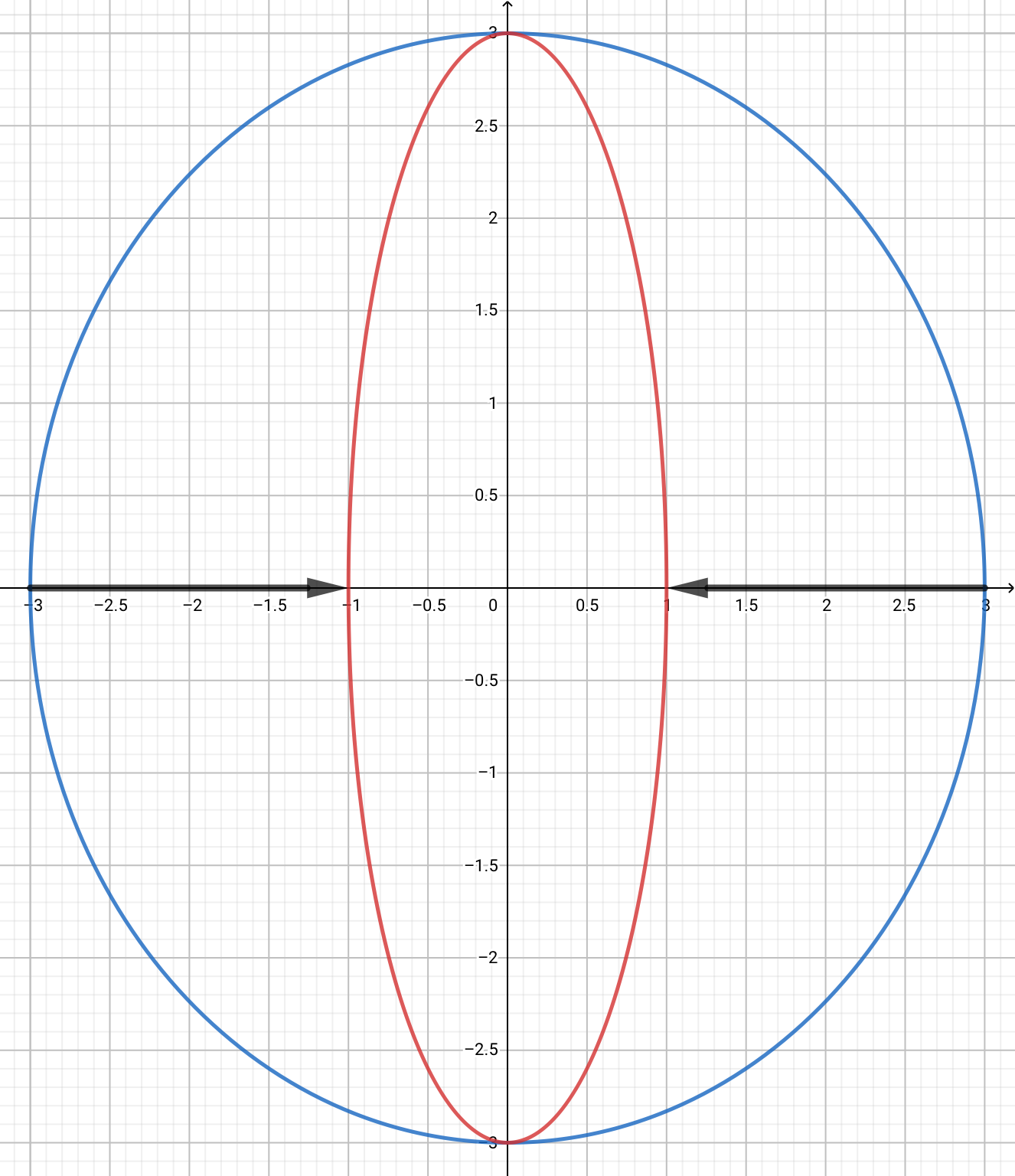
円を基準に考えるとだ円の方は\(x\)軸方向に\(1/3\)倍されたような形になっています。
これを式で表現してみましょう。
まず円の方程式は
x^2+y^2-9=0
\end{align}
とできるので、
f(x,y)=x^2+y^2-9
\end{align}
とおくと
f(x,y)=0
\end{align}
と表現することができますね。
ではだ円の方はどうでしょうか。ここで定義した関数\(f\)を使うとだ円の方程式を以下のように書き表すことができます。
f(3x,y)=0
\end{align}
マキノさんがパッと見で分からないのであれば、以下のように式変形をたどってみると実際にこれがだ円の方程式を表していることがわかります。
&f(3x,y)=0\\
\Longleftrightarrow
&9x^2+y^2-9=0\\
\Longleftrightarrow
&x^2+\frac{y^2}{9}-1=0\\
\Longleftrightarrow
&x^2+\frac{y^2}{9}=1
\end{align}
一般的には次のように言えます。
公式
f(x,y)=0
\end{align}
というグラフを\(x\)軸方向に\(a\)倍に拡大、\(y\)軸方向に\(b\)倍に拡大したものは
f(\frac{x}{a},\frac{y}{b})=0
\end{align}
である。ただし\(a>0, b>0\)とする。
例として見たものは縮小の例になっていましたが、縮小は分数倍の拡大と見てもいいので、一般的には拡大だけ理解しておけば問題ありません。
実際に\(x^2/a^2+y^2/b^2=1\)と\(x^2+y^2=r^2\)の面積を図で比較してみましょう。
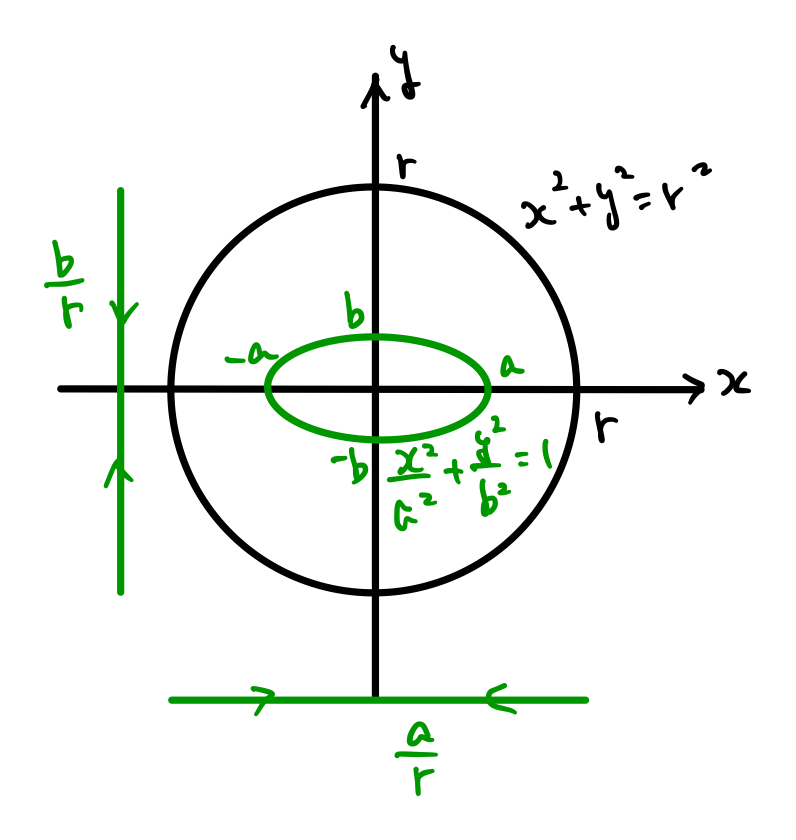
この図を見ると全て理解できるかなという感じだと思います。\(x^2+y^2=r^2\)の面積は\(\pi r^2\)です。
そこから、\(x\)軸方向には\(a/r\)倍、\(y\)軸方向には\(b/r\)倍したものが\(x^2/a^2+y^2/b^2=1\)ですから、面積は
\pi r^2\times \frac{a}{r}\times\frac{b}{r}=\pi a b
\end{align}
となります。
最後に1つだけ拡大と平行移動を合わせた問題を解いてこの節を終わります。
問題
y=2(x-1)^2+3
\end{align}
は\(y=x^2\)のグラフをどの方向にどれだけ拡大して、その後、いくら平行移動したものか答えよ。
解答
以下のように関数\(f\)を決めます。
f(x,y)=x^2-y
\end{align}
この\(f\)をどうにか拡大と並行移動をすることによって
2(x-1)^2-(y-3)=0
\end{align}
までもっていくのが問題の趣旨です。
まず、\(x^2\)の係数を2倍するには\(x\to\sqrt{2}x\)としなければなりませんね。そうすると
&f(\sqrt{2}x,y)=0\\
\Longleftrightarrow
&2x^2-y=0
\end{align}
までいきますね。あとは平行移動です。
目標の形と見比べると\((+1,+3)\)だけ平行移動すればいいことがわかります。
よって、最終的な答えは\(y=2(x-1)^2+3\)のグラフは\(y=x^2\)のグラフを\(x\)軸方向に\(1/\sqrt{2}\)倍して、\((+1,+3)\)だけ平行移動したものとなります。
ちょっと長くなっているのですが、最後に平方完成という技術だけ問題として扱っておきましょう。
解の公式を導くときに中学生でも習っているはずなので、それを思い出すだけです。
問題
以下の方程式を変形して、円を平行移動したものに見えるようにせよ。
x^2+6x+y^2+4x=0
\end{align}
解答
平方完成という技術自体はそれほど難しいものではありません。
まず前半の\(x^2+6x\)という部分に着目しましょう。
以下のように変形することができますね。
x^2+6x=(x+3)^2-9
\end{align}
左から右への変形が分からない場合は右から左へ変形すれば納得できると思います。
同様に
y^2+4x=(y+2)^2-4
\end{align}
とすることができます。
この変形を平方完成と言います。平方は2乗を意味しますから、無理やり2乗を作りにいく作業だと思っていただければそれで充分です。
さて、これらを用いると問題で与えられた方程式は以下のように変形できますね。
&x^2+6x+y^2+4x=0\\
\Longleftrightarrow
&(x+6)^2-9+(y+2)^2-4=0\\
\Longleftrightarrow
&(x+6)^2+(y+2)^2=13
\end{align}
これは半径\(\sqrt{13}\)で中心の座標が\((-6,-2)\)の円ということが分かります。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」








