(※数式が見切れている場合は横スクロールしてください。)
この節では具体例を考えるところから考えていきましょう。
それでは早速マキノさん、ボールを床に自由落下させると、ボールが跳ね返ってきて、ある程度まではもとの高さまで戻ってくるようなことを見たことはありますよね。
今回重要なのは「ある程度まで」という部分でして、自由落下させたボールが床で跳ね返ったとしても、基本的には完全にもとの高さまで戻ることはありません。
それはボールが床ではね返った直後には、はね返る直前よりもボールの速さが落ちているからです。
まず仮に、同じ速さではね返ったとすると本当に同じ高さに戻るのかを考えてみることにしましょう。
例
質点を水平面から高さ\(h\)の位置から自由落下させた。
はね返る直前と直後の質点の速さは同じで向きが逆向きになっていた場合、質点がもとの高さまで帰ってくることを確認せよ。
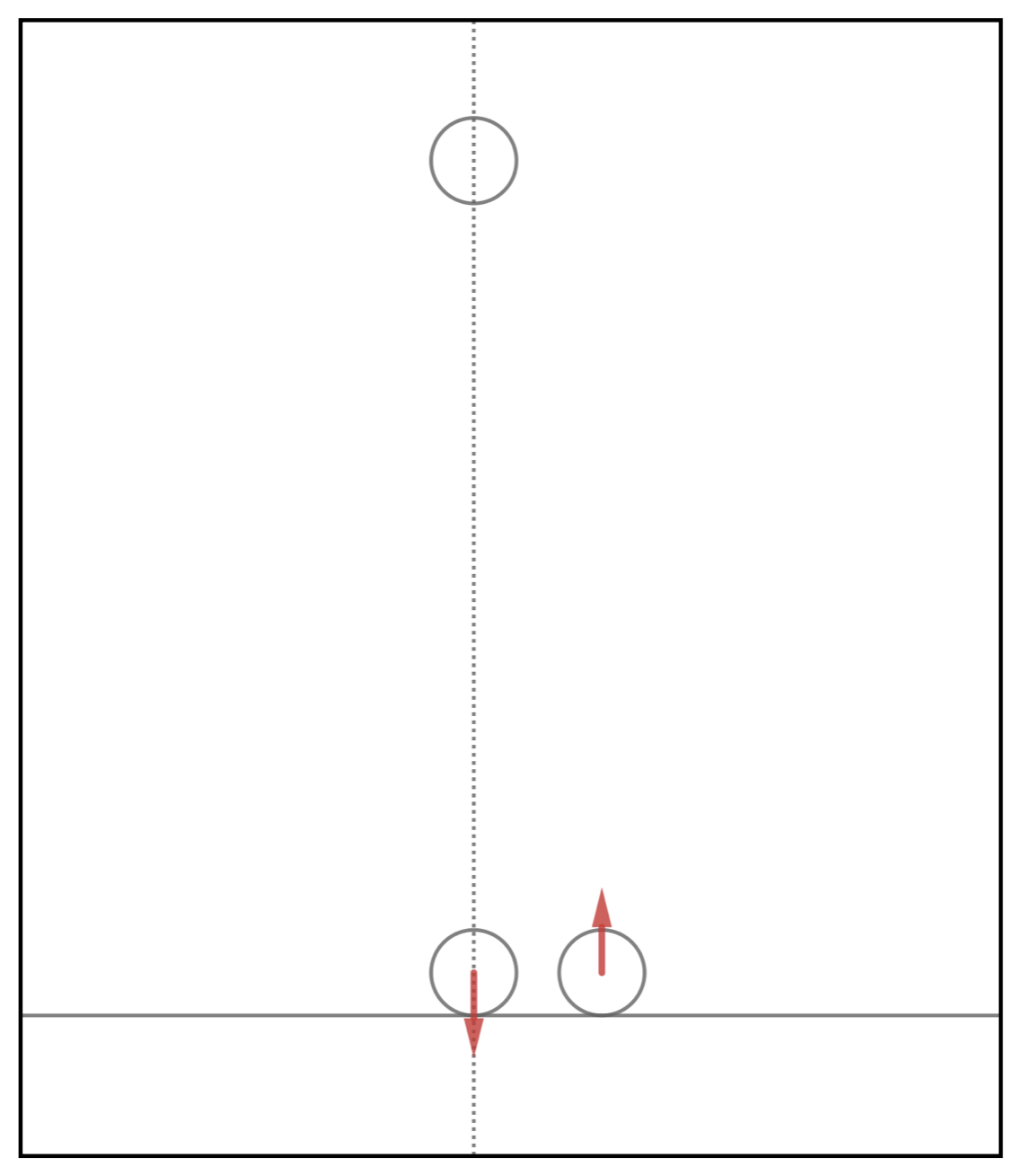
まずは高さ\(h\)から質点を落とすと床との衝突直前でどれだけの速さになるのかを計算します。
質点の質量を\(m\)とすると、運動方程式は
ma=-mg\quad\Longleftrightarrow\quad a=-g
\end{align}
ここでは、床面から上に向かって正の方向と考えることとしました。
床面を位置\(x=0\)とすると、加速度の時間積分と初期条件により、質点の位置と速度を以下のように時刻の関数で表すことができます。
&x(t)=h-\frac{1}{2}gt^2\\
&v(t)=-gt
\end{align}
質点が着地する時刻\(t_1\)をとすると、
x(t_1)=h-\frac{1}{2}gt^2=0\quad\Longleftrightarrow\quad t_1=\sqrt{\frac{2h}{g}}
\end{align}
となり、これを速度に代入すると、
v(t_1)=-\sqrt{2gh}
\end{align}
となります。
今度は、新たに時刻の軸を取り替えて、跳ね返った直後の時刻\(t’=0\)をとする時計を使いましょう。
そのときには質点の運動の初速度として
v(t’=0)=\sqrt{2gh}
\end{align}
が与えられています。そして、投げ上げたとしても、運動方程式の形が変わらないことから、この時計を使った時の質点の位置と速度の関数を以下のように書くことができます。
&x(t’)=\sqrt{2gh}t’-\frac{1}{2}gt’^2\\
&v(t’)=\sqrt{2gh}-gt’
\end{align}
質点が一番高い位置に来るときには速度がゼロになるはずですので、その時刻\(t_1’\)をとすると、
v(t’_1)=\sqrt{2gh}-gt_1’=0\quad\Longleftrightarrow\quad t’_1=\sqrt{\frac{2h}{g}}
\end{align}
これを先程の位置の関数に代入すると、
x(t’_1)=h
\end{align}
ともとの高さまで戻ることがわかります。
長々と計算を進めましたが、結局、はね返りの直前と直後で向きは逆になるけれども、速さの変わらない反射はもとの高さまで戻るということですね。
この節の最初に話しましたが、普通、自由落下した物体が床ではね返ってもとの高さまで戻ることはありえませんよね。ですので、今回のような「特殊な」衝突のことを弾性衝突という名前で呼びます。そうでない普通の衝突を非弾性衝突と言います。
では次に、同じシチュエーションで非弾性衝突だった場合について考えてみましょう。
非弾性衝突の場合には、衝突の前後で、どれだけ速さが変わったのかというのをはね返り定数という値を使って表現します。
例えば、はね返り定数を\(e\)とするとき\((0<e<1)\)、質点の床への衝突によって、その前後で質点の速さが\(e\)倍されるとしましょう。
このときに、どの高さまで元に戻るか計算してみましょう。
衝突する瞬間までは先ほどの例と同じですね。はね返り定数を入れると、衝突後の関数は形が変わってきます。
&x(t’)=e\sqrt{2gh}t’-\frac{1}{2}gt’^2\\
&v(t’)=e\sqrt{2gh}-gt’
\end{align}
さて、後の流れは先程と同様です。1番高いところに来た時には速さはゼロになります。そのときの時刻\(t’_2\)をとすると、
&v(t’_2)=e\sqrt{2gh}-gt’_2=0\\
\Longleftrightarrow &t’_2=e\sqrt{\frac{2h}{g}}
\end{align}
これをやはり位置の関数に代入すればいいわけですね。代入すると、
x(t’_2)=e^2h
\end{align}
という値が得られます。一回バウンドすると\(e^2\)で戻ってくる高さに効いてくるんですね。「〜で効く」という言い方もよく使う表現なので、覚えておくといいですね。
もう1度バウンドすると、次は1番最初のスタート位置、すなわち\(h\)に\(h\to e^2h\)という変換を行えば同じ議論が成り立ちますので、2回バウンドした後は\(e^4h\)の高さまでくるというわけですね。
はね返り係数は\(1\)よりも小さい正の数なので、はね返る度に最高到達点が下がっていき、最終的にははねなくなります。
ただし、この辺りは数列の極限の勉強をしてからまた改めて触れることにしますね。
では最後に1つ前の章の力積との関係を問題で扱ってこの節は終わりにしておきます。
問題
先程と同じ設定を採用する。すなわち高さ\(h\)の位置から床へ質点mを自由落下させる。床と質点のはね返り係数\(e\)をとしたとき、はね返り直前と、直後の質点の運動量を求め、それをヒントに床が質点に与えた力積を求めよ。
解答
先ほどまでの議論から、衝突直前と直後の質点の速さは分かっています。衝突直前の速度\(\vec{v_1}\)を、直後の速度を\(\vec{v_2}\)としてベクトル表記しておくと、
\vec{v_1}=\begin{pmatrix}0\\-\sqrt{2gh}\end{pmatrix},\quad\vec{v_2}=\begin{pmatrix}0\\e\sqrt{2gh}\end{pmatrix}
\end{align}
ここで、正負に注意が必要ですね。衝突の前後で運動の向きが変わっているので、\(y\)成分（床に対して垂直な方向）の正負は変わります。
速度ベクトルが分かっていれば、それに質量をかけたものが運動量なので、衝突直前の運動量を\(\vec{p_1}\)とし、衝突直後の運動量を\(\vec{p_2}\)とすると、
\vec{p_1}=\begin{pmatrix}0\\-m\sqrt{2gh}\end{pmatrix},\quad\vec{p_2}=\begin{pmatrix}0\\me\sqrt{2gh}\end{pmatrix}
\end{align}
となります。運動量の変化が力積なので、床が質点に与えた力積は
\vec{p_2}-\vec{p_1}=\begin{pmatrix}0\\me\sqrt{2gh}\end{pmatrix}-\begin{pmatrix}0\\-m\sqrt{2gh}\end{pmatrix}=\begin{pmatrix}0\\m(e+1)\sqrt{2gh}\end{pmatrix}
\end{align}
と求められます。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」
東大理系攻略法を
解説したPDF販売中！
中高一貫校に行かなくても、塾に行かなくても、独学で受かるための勉強法を完全解説！
全科目の参考書
全参考書の使い方
受験までの勉強スケジュール
が全てわかります！
今だけ！100様限定60%OFF！
さらに24時間以内なら返金保証つき！
無料サンプル公開！
