(※数式が見切れている場合は横スクロールしてください。)
だ円の次は双曲線です。惑星がだ円軌道を描くことだけを勉強したかったら、関係ないのですが、この機会に学んでおくといい内容なので、しっかり理解していきましょう。
だ円軌道上の点Pと焦点FとF’の関係は以下のようなものでした。
PF+PF’=const.
\end{align}
右辺は定数を表しています。焦点からの距離の和が定数の点を集めるとだ円になるということですね。
双曲線に関してはこの関係を少し変形して
\left|PF-PF’\right|=const.
\end{align}
とします。
左辺の\(|\quad|\)は絶対値記号です。絶対値に関しては簡単なことは中学数学でも習う内容ですが、一応説明しておきます。
絶対値記号の中身が正ならそのまま中身を返し、
中身が負なら符号を変えて中身を返してきます。例えば、以下のような感じです。
&\left|-2\right|=2\\
&\left|a\right|=\begin{cases}a\quad (a\geq 0)\\
-a\quad(a\leq 0)\end{cases}
\end{align}
焦点FとF’からの距離の差が定数となる点Pを集めてくると双曲線が描かれるということです。
もとの双曲線の条件に戻って、\(\left|PF-PF’\right|\)はPFとPF’の差を表すんです。
PFの方が大きかったら、そのまま絶対値を外しますし、
PF’の方が大きかったら、絶対値の中身にマイナスをつけてPF’からPFを引く形になりますね。
というわけで具体的に双曲線の方程式を考えていきましょう。
例
点F\((c,0)\)、点F’\((-c,0)\)のとき、点P\((x,y)\)が以下の式を満たすとする。
\left|PF-PF’\right|=2a
\end{align}
\(a\)は正の定数で\(c>a\)とする。
このときの\((x,y)\)の関係を示せ。
だ円のときと同様に2乗してルートを消していく方針で計算をしていけばいいだけです。
絶対値を外すときに以下のように書けば、中身の正負による場合分けを同時に考慮することができます。
PF-PF’=\pm2a
\end{align}
これを使って計算を進めていくことにしましょう。
まずは図でイメージをつかんでください。
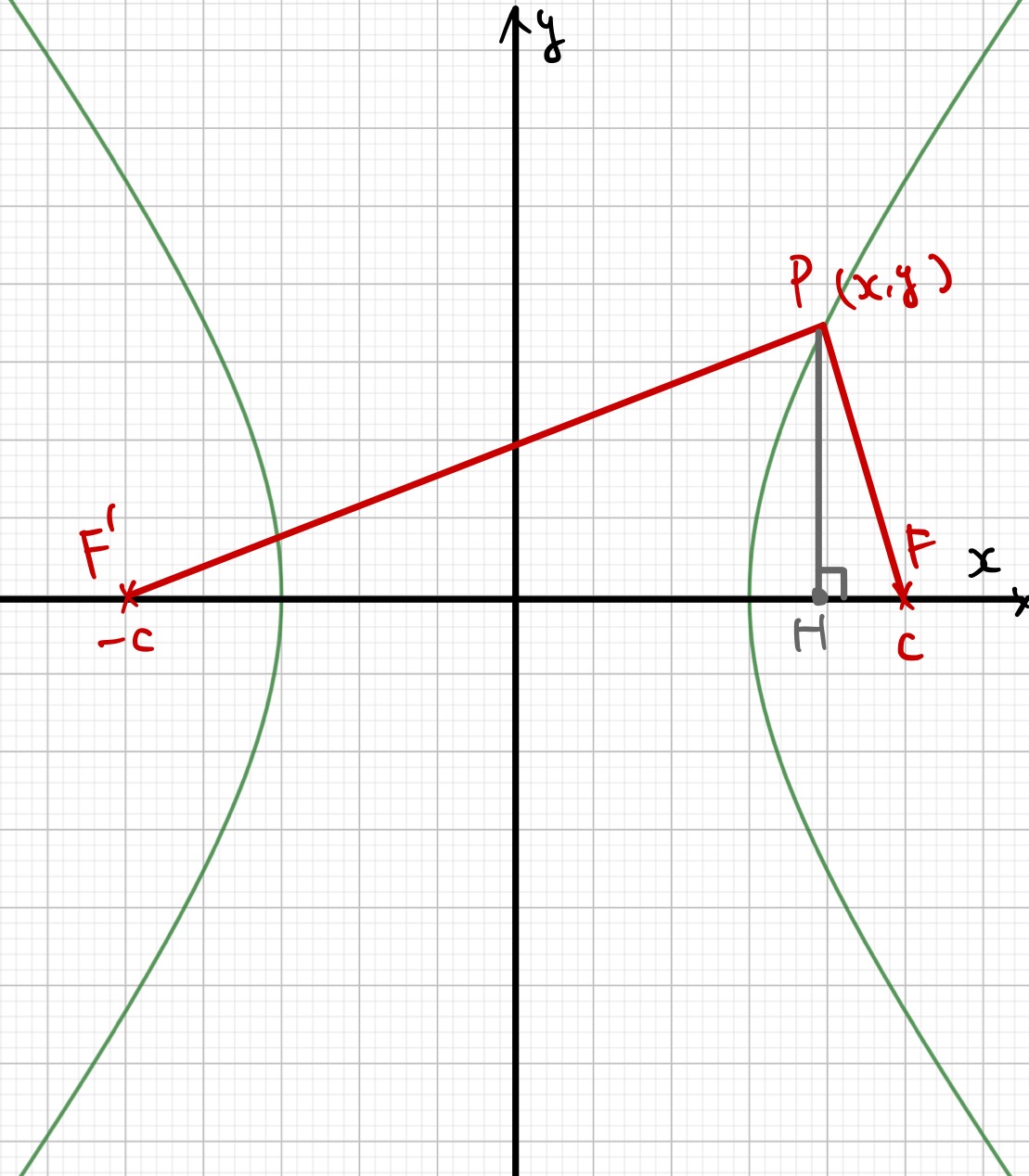
この図から
&PF-PF’=\pm2a\\
\Longleftrightarrow
&\sqrt{(x-c)^2+y^2}-\sqrt{(x+c)^2+y^2}=\pm2a
\end{align}
です。あとはルートを消すように計算していくだけです。
計算の過程はだ円の時とほとんど同じです。
この図から
&\sqrt{(x-c)^2+y^2}-\sqrt{(x+c)^2+y^2}=\pm2a\\
\Longleftrightarrow
&(x-c)^2+y^2=4a^2\pm4a\sqrt{(x+c)^2+y^2}+(x+c)^2+y^2\\
\Longleftrightarrow
&-cx=a^2\pm a\sqrt{(x+c)^2+y^2}\\
\Longleftrightarrow
&-cx-a^2=\pm a\sqrt{(x+c)^2+y^2}\\
\Longleftrightarrow
&c^2x^2+2a^2cx+a^4=a^2\left((x+c)^2+y^2\right)\\
\Longleftrightarrow
&(a^2-c^2)x^2+a^2y^2=a^2(a^2-c^2)
\end{align}
ここで\(c>a\)なので、\(c^2-a^2=b^2\)とおくと、
&(a^2-c^2)x^2+a^2y^2=a^2(a^2-c^2)\\
\Longleftrightarrow
&-b^2x^2+a^2y^2=-a^2b^2\\
\Longleftrightarrow
&\frac{x^2}{a^2}-\frac{y^2}{b^2}=1
\end{align}
まとめておきましょう。
公式
次の方程式
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1
\end{align}
は双曲線を表し、焦点は\((\pm\sqrt{a^2+b^2},0)\)となる。
また、
-\frac{x^2}{a^2}+\frac{y^2}{b^2}=1
\end{align}
も双曲線を表し、焦点は\((0,\pm\sqrt{a^2+b^2})\)となる。
では問題を見ておきましょう。
問題
以下の双曲線の焦点を計算し、グラフをかけ。
\frac{x^2}{3^2}-\frac{y^2}{4^2}=1
\end{align}
解答
焦点は公式から一瞬で計算できますね。
\sqrt{3^2+4^2}=5
\end{align}
なので、焦点は\((\pm5,0)\)です。
グラフは以下のような形になります。
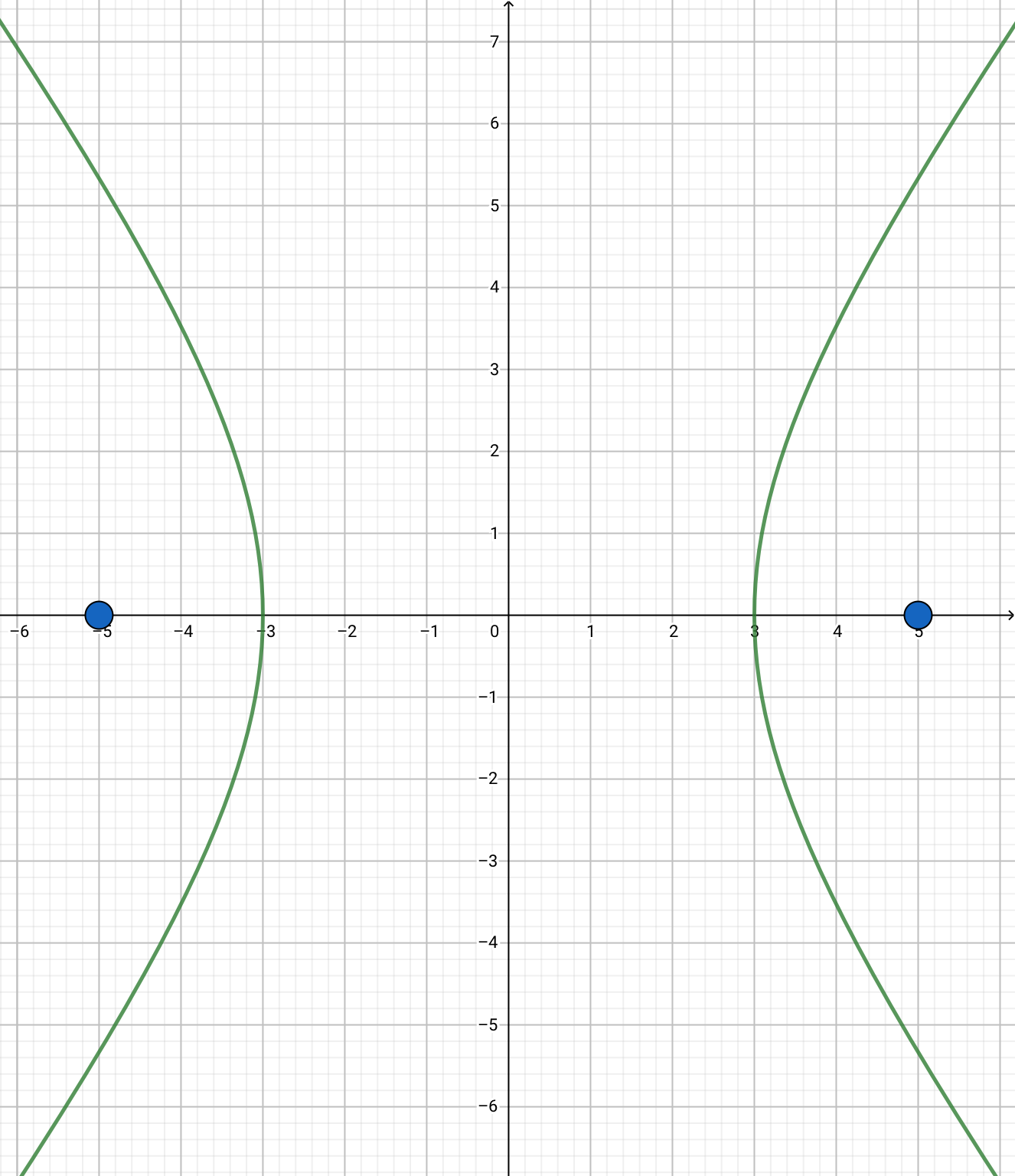
グラフの書き方のポイントとしてはやはり\(x=0\)や\(y=0\)の条件を代入してみることです。
この問題の場合だと\(x=0\)を代入すると双曲線の方程式は左辺と右辺の正負が一致しませんから、その条件を満たす\(y\)は存在しません。
よって、\(x=0\)すなわち\(y\)軸は通らないです。
今度は\(y=0\)を入れてみると、\(x=\pm3\)で図形の方程式を満たしますから、双曲線は\((\pm3,0)\)を通ることとなります。
これをヒントにグラフを描くのがポイントですね。
ちなみに\(-x^2/3^2+y^2/4^2=1\)のときには\((0,\pm4)\)を通って上下にグラフが開く形になります。
最後におまけです。
公式
双曲線の方程式が以下のようにあらわされるとき、
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1
\end{align}
その双曲線の漸近線は
\frac{x}{a}\pm\frac{y}{b}=0
\end{align}
の2本となる。
漸近線というのはある極限において、図形の方程式が近づいていく直線の方程式です。
上の図を見ると\(x\to\infty\)の極限で、双曲線が段々と漸近線に近づいていく様子がわかります。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」
東大理系攻略法を
解説したPDF販売中！
中高一貫校に行かなくても、塾に行かなくても、独学で受かるための勉強法を完全解説！
全科目の参考書
全参考書の使い方
受験までの勉強スケジュール
が全てわかります！
今だけ！100様限定60%OFF！
さらに24時間以内なら返金保証つき！
無料サンプル公開！
