極座標表示での図形の方程式

(※数式が見切れている場合は横スクロールしてください。)
この節では極座標表示で図形の方程式をいくつか見ておきましょう。
1つ目としては直線の方程式です。
直線の方程式として
y=(\tan\alpha)x+\beta
\end{align}
を極座標表示に変えてみます。この直線は図としてはこんな形になります。
傾きは\(\tan\)で表現していますが、\(tan\)の定義を考えたらそれほど特殊ではないですよね。
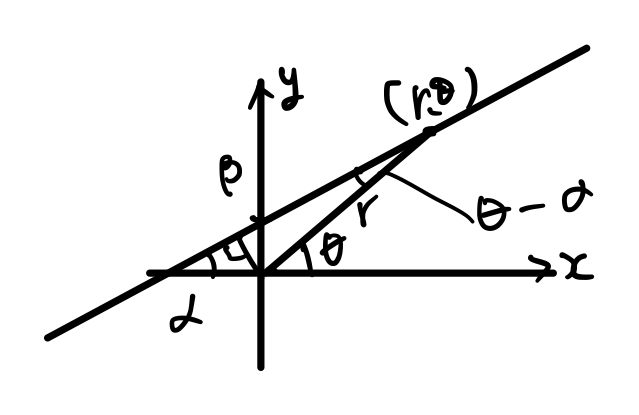
実際には\(x\)を\(r\cos\theta\)にして\(y\)を\(r\sin\theta\)に変えるだけです。
&r\sin\theta=(\tan\alpha) r\sin\theta +\beta\\
\Longleftrightarrow
&r\sin\theta\cos\alpha=r\cos\theta\sin\theta+\beta \cos\alpha\\
\Longleftrightarrow
&r\left(\sin\theta\cos\alpha-\cos\theta\sin\theta\right)=\beta \cos\alpha\\
\Longleftrightarrow
&r\sin(\theta-\alpha)=\beta\cos\alpha
\end{align}
最後の変形には三角関数の加法定理を使いました。
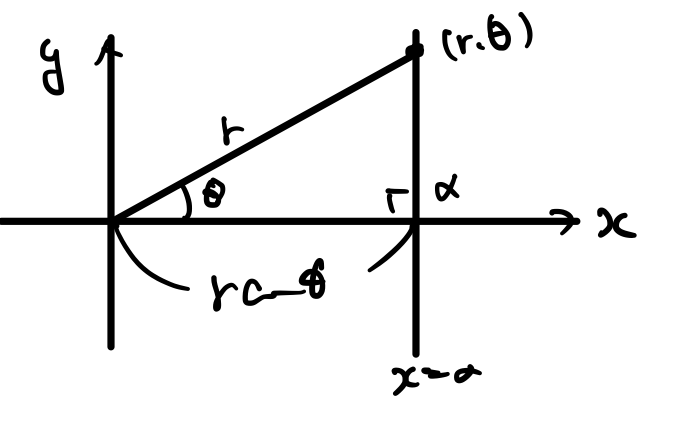
もう1つ\(x=\alpha\)という直線も極座標表示にしてみましょう。
&x=\alpha\\
\Longleftrightarrow
&r\cos\theta=\alpha
\end{align}
問題
\(y=\sqrt{3}x\)を極座標表示で表現せよ。
解答
\(x\)を\(r\cos\theta\)にして\(y\)を\(r\sin\theta\)に変えると
&r\sin\theta=\sqrt{3}\cdot r\cos\theta\\
\Longleftrightarrow
&\theta=\frac{\pi}{3}
\end{align}
原点を通る直線なら\(\theta=\alpha\)という形で直線を表示できることがわかります。
次は円に移りましょう。まずは原点を中心とする半径\(R\)の円\(x^2+y^2=R^2\)は
x^2+y^2=R^2\\
\Longleftrightarrow
r^2\cos^2\theta+r^2\sin^2\theta=R^2\\
\Longleftrightarrow
r=R
\end{align}
となります。半径だけ言ってやればそれで原点中心の円が指定できます。
次は原点を通る円ですね。これは図形的な考え方を意識して考えると分かりやすいかもしれません。
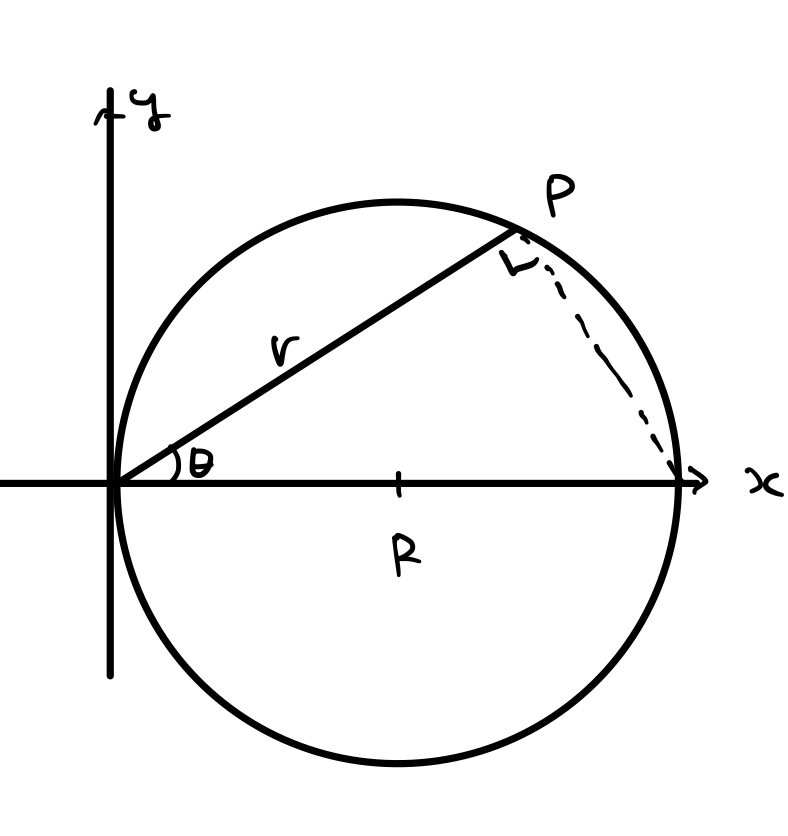
図形をもとに考えると、常に以下の関係式を満たすのがわかります。
r\cos\theta=2R
\end{align}
最後は原点を焦点とする2次曲線です。
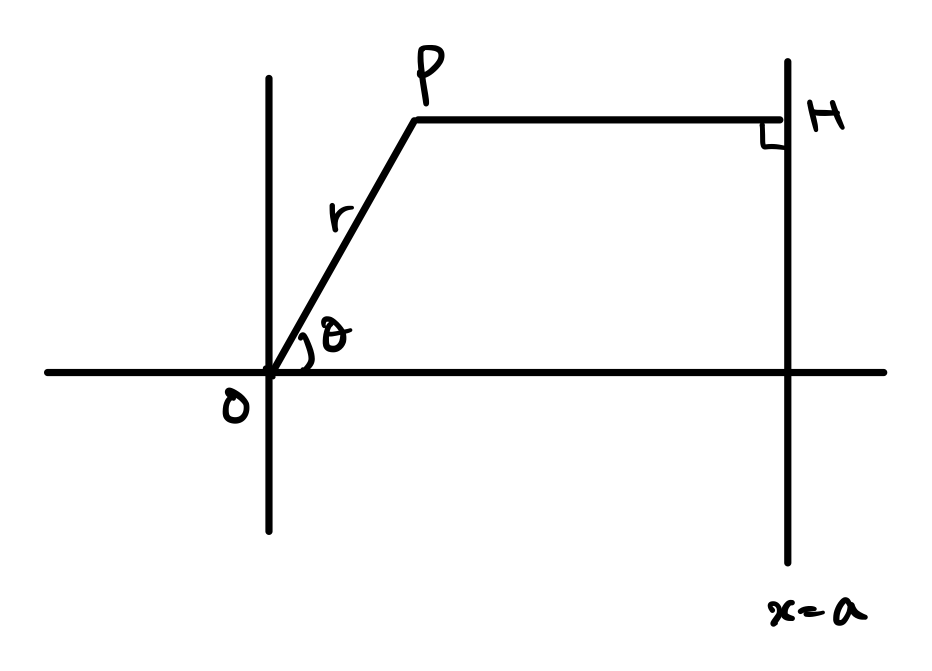
点Pは\(r,\theta\)によって指定される点で、準線を\(x=a\)、焦点を原点とします。
準線と点Pの距離、原点と点Pとの距離の比を\(1:e\)として計算を以下のように進めます。
&PH:OP=a-r\cos\theta:r=1:e\\
\Longleftrightarrow
&r=\frac{ea}{1+e\cos\theta}
\end{align}
となります。
もちろん、\(0<e<1\)でだ円、\(e=1\)で放物線、\(e>1\)で双曲線となるのは極座標表示でも同じです。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」








