重心系で考える

(※数式が見切れている場合は横スクロールしてください。)
まずベクトル表記で重心について考えてみましょう。
質量\(m_1\)の質点1が位置\(\vec{x_1}\)にあり、質量\(m_2\)の質点2が位置\(\vec{x_2}\)にあるとき、重心の位置\(\vec{x_G}\)は以下のようになります。
\vec{x_G}=\frac{m_1\vec{x_1}+m_2\vec{x_2}}{m_1+m_2}
\end{align}
全質量\(m_1+m_2\)に対して、\(m_1\)分だけ\(\vec{x_1}\)の所に寄与があって、\(m_2\)分だけ\(\vec{x_2}\)の所に寄与があるというイメージです。
ちなみにn個の質点があるときには、重心\(\vec{x_G}\)は次のような形になります。
\vec{x_G}=\frac{m_1\vec{x_1}+m_2\vec{x_2}+\cdots+m_n\vec{x_n}}{m_1+m_2+\cdots+m_n}
\end{align}
重心の位置ベクトル\(\vec{x_G}\)に関して言うと、質点の集まりに外力が掛かっていないときには、
\dot{\vec{x_G}}=\frac{m_1\dot{\vec{x_1}}+m_2\dot{\vec{x_2}}+\cdots+m_n\dot{\vec{x_n}}}{m_1+m_2+\cdots+m_n}
\end{align}
の分子が運動量保存則で時間に依らないことがわかります。
重心系でものを見て運動を考察するという練習をしてみましょう。
例
以下のようにばねkにつながれた質量\(m\)の質点Aと質点Bを自然長の長さで置いておく。
\(t=0\)に置いて、質点Bに初速度\(v_0\)を与えると以降の質点Aと質点Bの運動はどのようになるか。
運動を見ている間、ばねの弾性力以外に力はかかっていないとする。
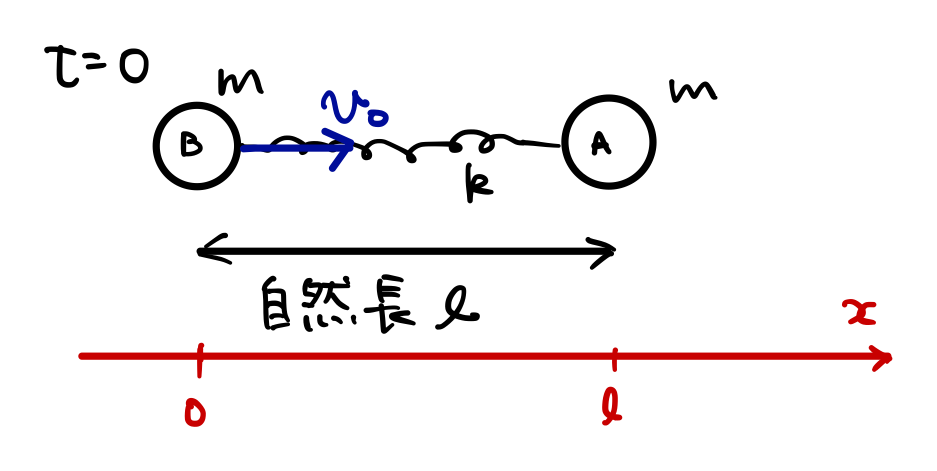
外力が働いていないので、重心は等速運動します。
重心の位置を\(x_G(t)\)とすると、
&x_G(0)=\frac{l}{2}\\
&x_G(t)=\frac{x_A(t)}{2}+\frac{x_B(t)}{2}\\
&\dot{x_G}(0)=\frac{v_0}{2}\\
&\dot{x_G}(t)=0
\end{cases}\end{align}
というのが瞬時にわかります。ここで、\(x_A\)と\(x_B\)はもちろん質点Aと質点Bの位置です。
これらの情報から重心についてはすぐに運動の様子を以下のように記述できます。
&\dot{x_G}(t)=v_0\\
&x_G(t)=\frac{l}{2}+v_0t
\end{cases}\end{align}
全体の縮みは自然長\(l\)から、\(x_A-x_B\)を引き算したものと考えると次のような図が描けます。
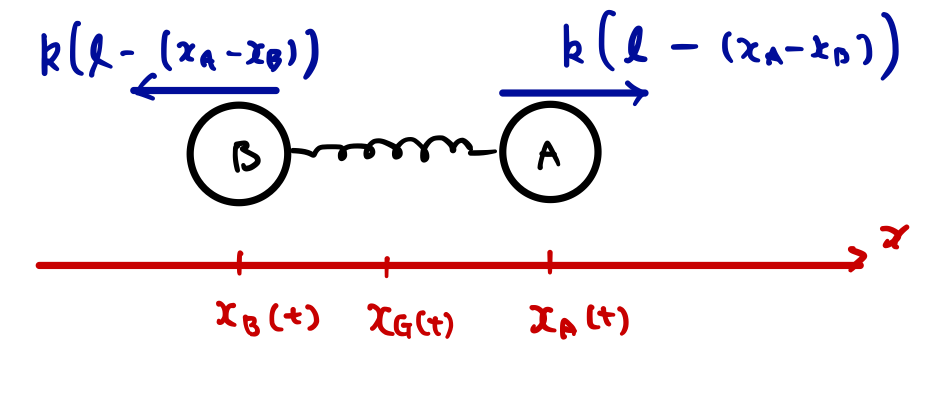
質点Aの運動方程式は次のようになります。
m\ddot{x_A}=k(l-x_A+x_B)
\end{align}
これを解こうと思うと、\(x_B\)が邪魔になってしまいます。が、重心を絡めて\(x_B\)を消してしまうのがコツです。
&x_G=\frac{x_A}{2}+\frac{x_B}{2}\\
\Longleftrightarrow
&x_B=2x_G-x_A
\end{align}
これを運動方程式に代入してみると、
m\ddot{x_A}=k(l-2x_A+2x_G)
\end{align}
となりますが、このままでは少し大変です。コツは重心系でものを見ることです。重心から見た質点Aの相対座標を\(X_A(=x_A-x_G)\)とすると、以下のように書き換えられます。
&m\ddot{X_A+x_G}=k(l-2X_A)\\
\Longleftrightarrow
&m\ddot{X_A}=-2k(X_A-\frac{l}{2})\\
\Longleftrightarrow
&m\frac{d^2}{dt^2}\left(X_A-\frac{l}{2}\right)=-2k(X_A-\frac{l}{2})
\end{align}
\(x_G\)の2回微分がゼロであることを使いました。ここまでくると、単振動の方程式になっています。
初速度と初期位置に注意すると、相対座標はすぐに解けます。
&X_A(0)-\frac{l}{2}=0\\
&\dot{X_A}(0)=-\frac{v_0}{2}
\end{align}
Bに\(v_0\)を与えた瞬間にAの重心に対する相対速度としては負になることに注意です。
X_A=\frac{l}{2}+\frac{v_0}{2}\sqrt{\frac{m}{2k}}\sin\sqrt{\frac{2k}{m}}t
\end{align}
よって、\(x_A\)に関してもこれを使えばわかります。
x_A=&X_A+x_G\\
=&\frac{l}{2}+\frac{v_0}{2}\sqrt{\frac{m}{2k}}\sin\sqrt{\frac{2k}{m}}t+\frac{l}{2}+v_0t\\
=&l+v_0t+\frac{v_0}{2}\sqrt{\frac{m}{2k}}\sin\sqrt{\frac{2k}{m}}t
\end{align}
少し難しい問題でしたが、このように重心に乗った系で運動を見ると、\(v_0t\)のような等速運動成分をカット出来て、単純な単振動として運動を見ることができます。
同じように質点Bの運動も考えることができるので、ぜひマキノさんも考えてみてください。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」






