(※数式が見切れている場合は横スクロールしてください。)
少し数学的になりますが、中心力が保存力であることを証明しておきましょう。
初見だと難しく感じるかもしれませんが、マキノさんが難しく感じるようでしたら、一旦飛ばしていただいても構いません。
ではさっそく考えていきましょう。
まず図のように原点Oからの距離\(r_p\)の点Pから、同じく原点からの距離\(r_Q\)の経路\(C\)を通って質点ｍが移動する状況を考えます。
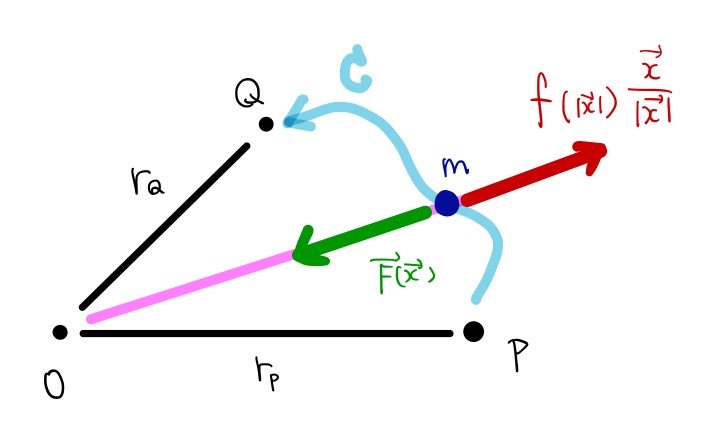
移動の間の質点ｍの位置をベクトル\(\vec{x}(t)\)で表現することにしましょう。
移動の書く瞬間で質点ｍは中心力\(f(\left|\vec{x}(t)\right|)\vec{x}(t)/\left|\vec{x}(t)\right|\)を受けてそれに逆らう外力\(\vec{F}(t)\)をmに加えてゆっくり移動させます。
中心力の大きさは\(f(\left|\vec{x}(t)\right|)\)の部分が担当していて、向きは\(\vec{x}(t)/\left|\vec{x}(t)\right|\)の部分が担当しています。
大きさは原点からの距離だけに依存していますね。
この外力\(\vec{F}(t)\)がする仕事を計算した結果、スタート地点Pとゴール地点Qの情報だけで仕事が記述できて、
経路\(C\)の情報が必要ないことが言えれば、中心力は保存力であるということが言えます。
外力は中心力にあらがうためのものなので、中心力と大きさは同じで向きは逆です。
\vec{F}(t)=-f(\left|\vec{x}(t)\right|)\frac{\vec{x}(t)}{\left|\vec{x}(t)\right|}
\end{align}
この外力のする仕事\(W\)は以下のようになります。
W=\int^{t_Q}_{t_P}\vec{F}(t)\cdot \dot{\vec{x}}(t)dt\\
\end{align}
ここで、時刻\(t_P\)は点Pの位置に質点ｍがあるときの時刻、時刻\(t_Q\)は点Pの位置に質点ｍがあるときの時刻です。
次に具体的に仕事の積分の計算を進めていくことにしますね。外力に中心力の形を入れると
W=-\int^{t_Q}_{t_P} f(\left|\vec{x}(t)\right|)\frac{\vec{x}(t)}{\left|\vec{x}(t)\right|}\cdot\dot{\vec{x}}(t)dt
\end{align}
となります。ここで\(\vec{x}(t)\cdot\dot{\vec{x}}(t)\)に着目して以下のような変形を使います。
\vec{x}(t)\cdot\dot{\vec{x}}(t)=&\frac{1}{2}\left(\vec{x}(t)\cdot\dot{\vec{x}}(t)+\dot{\vec{x}}(t)\cdot\vec{x}(t)\right)\\
=&\frac{1}{2}\frac{d}{dt}\left(\vec{x}(t)\cdot\vec{x}(t)\right)\\
=&\frac{1}{2}\frac{d}{dt}\left|\vec{x}(t)\right|^2\\
=&\frac{1}{2}\cdot 2\left|\vec{x}(t)\right|\cdot\frac{d}{dt}\left|\vec{x}(t)\right|\\
=&\left|\vec{x}(t)\right|\frac{d}{dt}\left|\vec{x}(t)\right|
\end{align}
これをもとの仕事の積分の計算に入れなおしてみると
W=-\int^{t_Q}_{t_P} f(\left|\vec{x}(t)\right|)\left(\frac{d}{dt}\left|\vec{x}(t)\right|\right)dt
\end{align}
と書きなおせますね。ここで\(t\to r=\left|\vec{x}(t)\right|\)と変数変換をします。
このとき、積分区間は
\begin{cases}
t:t_P\to t_Q\\
r:r_P\to r_Q
\end{cases}
\end{align}
となります。また、微小幅は以下のようになります。
\frac{dr}{dt}=\frac{d}{dt}\left|\vec{x}(t)\right|\\
\Longleftrightarrow
dr=\frac{d}{dt}\left|\vec{x}(t)\right|dt
\end{align}
これらを使うと仕事は最終的に以下のようになります。
W=-\int^{r_Q}_{r_P}f(r)dr
\end{align}
\(f\)の原始関数\(U\)を以下のように決めると
\int f(r)dr=-U(r)+C
\end{align}
最終的には仕事は
W=U(r_Q)-U(r_P)
\end{align}
となります。中心力に逆らって外力\(vec{F}(t)\)のした仕事はスタート位置の情報\(r_P\)とゴール位置の情報\(r_Q\)だけで記述できることがわかりました。
よって中心力は保存力であることを証明できました。
ところで、\(U(r)\)は中心力によるポテンシャルエネルギーです。
中心力によるポテンシャルエネルギーは、中心力と同じで、原点からの距離だけで決まる関数になっています。
これは対称性を持っている状態で、3次元で考えるのであれば球と同じ対称性を持っていると言えます。
たとえば、\(\vec{x_1}\)、\(\vec{x_2}\)を以下のように与えられている時、
&\vec{x_1}=\begin{pmatrix}1\\0\\0\end{pmatrix}\\
&\vec{x_2}=\begin{pmatrix}0\\1\\0\end{pmatrix}
\end{align}
もちろん対称性からこれを\(U\)に入れると、同じポテンシャルエネルギーの値が返ってくるということです。
2次元のときには円と同じ対称性となりますね。これらは回転対称性の一部となります。
1次元のときには回転はできませんが、反転対称性があるということですね。
さて話を戻してきます。
ポテンシャルエネルギーの決め方は
\int f(r)dr=-U(r)+C
\end{align}
と決めてました。右辺はマイナスをつけていることが大事です。
仕事\(W\)を計算した最終結果を変形すると
U(r_P)+W=U(r_Q)
\end{align}
という形になります。左辺はスタート地点のポテンシャルエネルギーに外力のした仕事を足したものです。
スタート地点でのポテンシャルエネルギーに外力のする仕事を足した結果が、右辺のゴール地点でのポテンシャルエネルギーの値になるということです。
エネルギーの変化が外力のした仕事になっているのが、この形にすると見えやすいですね。
今回、\(U(r)\)を決めるときに、積分定数\(C\)の不定性が残っているのが見えますね。
これはポテンシャルエネルギーの絶対量が重要な意味を持っているのではなく、ポテンシャルエネルギーの変化量やその微分に重要な意味を持っていることを意味します。
言い換えると、ポテンシャルエネルギーの基準の位置は任意に選んでも構わないということです。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」
東大理系攻略法を
解説したPDF販売中！
中高一貫校に行かなくても、塾に行かなくても、独学で受かるための勉強法を完全解説！
全科目の参考書
全参考書の使い方
受験までの勉強スケジュール
が全てわかります！
今だけ！100様限定60%OFF！
さらに24時間以内なら返金保証つき！
無料サンプル公開！
