(※数式が見切れている場合は横スクロールしてください。)
ある時刻に質点が以下のような速度\(\vec{v}\)を持っているとしましょう。
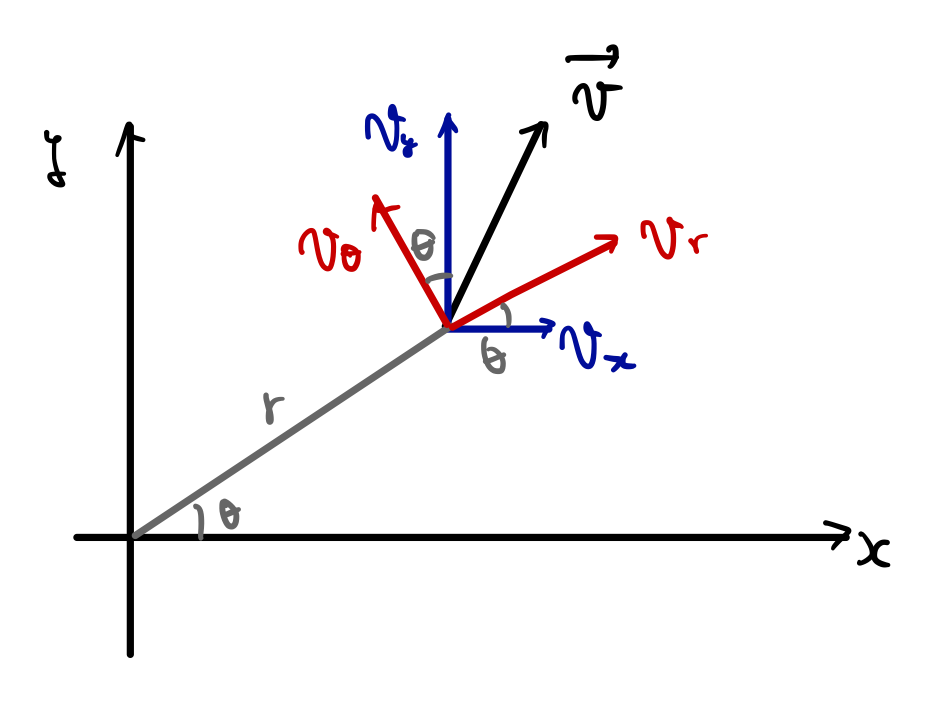
\(xy\)表示での分解はここまで勉強してきたマキノさんなら慣れていらっしゃるで章から、メインは\(r\theta\)表示との対応を考えることです。
上の図を参考に考えると以下のような関係にあることがわかります。
\begin{align}
\begin{cases}
v_r=v_x\cos\theta+v_y\sin\theta\\
v_\theta=-v_x\sin\theta+v_y\cos\theta
\end{cases}
\end{align}
\begin{cases}
v_r=v_x\cos\theta+v_y\sin\theta\\
v_\theta=-v_x\sin\theta+v_y\cos\theta
\end{cases}
\end{align}
ついでに\(v_x\)と\(v_y\)も\(r\theta\)表示してみましょう。
\begin{align}
v_x=&\frac{d}{dt}(r\cos\theta)\\
=&\dot{r}\cos\theta-r\dot{\theta}\sin\theta\\
v_y=&\frac{d}{dt}(r\sin\theta)\\
=&\dot{r}\sin\theta+r\dot{\theta}\cos\theta
\end{align}
v_x=&\frac{d}{dt}(r\cos\theta)\\
=&\dot{r}\cos\theta-r\dot{\theta}\sin\theta\\
v_y=&\frac{d}{dt}(r\sin\theta)\\
=&\dot{r}\sin\theta+r\dot{\theta}\cos\theta
\end{align}
となります。これを先ほどの\(v_r\)と\(v_\theta\)に入れると以下のようになります。
\begin{align}
v_r=&(\dot{r}\cos\theta-r\dot{\theta}\sin\theta)\cos\theta+(\dot{r}\sin\theta+r\dot{\theta}\cos\theta)\sin\theta\\
=&\dot{r}\\
v_\theta=&-(\dot{r}\cos\theta-r\dot{\theta}\sin\theta)\sin\theta+(\dot{r}\sin\theta+r\dot{\theta}\cos\theta)\cos\theta\\
=&r\dot{\theta}
\end{align}
v_r=&(\dot{r}\cos\theta-r\dot{\theta}\sin\theta)\cos\theta+(\dot{r}\sin\theta+r\dot{\theta}\cos\theta)\sin\theta\\
=&\dot{r}\\
v_\theta=&-(\dot{r}\cos\theta-r\dot{\theta}\sin\theta)\sin\theta+(\dot{r}\sin\theta+r\dot{\theta}\cos\theta)\cos\theta\\
=&r\dot{\theta}
\end{align}
これと同じように加速度を計算してしまいましょう。
まず加速度\(a_r\)と\(a_\theta\)を\(a_x\)と\(a_y\)で表現します。
\begin{align}
\begin{cases}
a_r=a_x\cos\theta+a_y\sin\theta\\
a_\theta=-a_x\sin\theta+a_y\cos\theta
\end{cases}
\end{align}
\begin{cases}
a_r=a_x\cos\theta+a_y\sin\theta\\
a_\theta=-a_x\sin\theta+a_y\cos\theta
\end{cases}
\end{align}
この\(a_x\)と\(a_y\)も改めて\(r\theta\)表示してしまえばいいですね。
\begin{align}
a_x=&\frac{d}{dt}v_x=\frac{d}{dt}(\dot{r}\cos\theta-r\dot{\theta}\sin\theta)\\
=&\ddot{r}\cos\theta-2\dot{r}\dot{\theta}\sin\theta-r\dot{\theta}^2\cos\theta-r\ddot{\theta}\sin\theta\\
a_y=&\frac{d}{dt}v_y=\frac{d}{dt}(\dot{r}\sin\theta+r\dot{\theta}\cos\theta)\\
=&\ddot{r}\sin\theta+2\dot{r}\dot{\theta}\cos\theta-r\dot{\theta}^2\sin\theta+r\ddot{\theta}\cos\theta
\end{align}
a_x=&\frac{d}{dt}v_x=\frac{d}{dt}(\dot{r}\cos\theta-r\dot{\theta}\sin\theta)\\
=&\ddot{r}\cos\theta-2\dot{r}\dot{\theta}\sin\theta-r\dot{\theta}^2\cos\theta-r\ddot{\theta}\sin\theta\\
a_y=&\frac{d}{dt}v_y=\frac{d}{dt}(\dot{r}\sin\theta+r\dot{\theta}\cos\theta)\\
=&\ddot{r}\sin\theta+2\dot{r}\dot{\theta}\cos\theta-r\dot{\theta}^2\sin\theta+r\ddot{\theta}\cos\theta
\end{align}
これを先ほどの式に代入して
\begin{align}
a_r=&(\ddot{r}\cos\theta-2\dot{r}\dot{\theta}\sin\theta-r\dot{\theta}^2\cos\theta-r\ddot{\theta}\sin\theta)\cos\theta+(\ddot{r}\sin\theta+2\dot{r}\dot{\theta}\cos\theta-r\dot{\theta}^2\sin\theta+r\ddot{\theta}\cos\theta)\sin\theta\\
=&\ddot{r}-r\dot{\theta}^2\\
a_\theta=&-(\ddot{r}\cos\theta-2\dot{r}\dot{\theta}\sin\theta-r\dot{\theta}^2\cos\theta-r\ddot{\theta}\sin\theta)\sin\theta+(\ddot{r}\sin\theta+2\dot{r}\dot{\theta}\cos\theta-r\dot{\theta}^2\sin\theta+r\ddot{\theta}\cos\theta)\cos\theta\\
=&2\dot{r}\dot{\theta}+r\ddot{\theta}=\frac{1}{r}\frac{d}{dt}(r^2\dot{\theta})
\end{align}
a_r=&(\ddot{r}\cos\theta-2\dot{r}\dot{\theta}\sin\theta-r\dot{\theta}^2\cos\theta-r\ddot{\theta}\sin\theta)\cos\theta+(\ddot{r}\sin\theta+2\dot{r}\dot{\theta}\cos\theta-r\dot{\theta}^2\sin\theta+r\ddot{\theta}\cos\theta)\sin\theta\\
=&\ddot{r}-r\dot{\theta}^2\\
a_\theta=&-(\ddot{r}\cos\theta-2\dot{r}\dot{\theta}\sin\theta-r\dot{\theta}^2\cos\theta-r\ddot{\theta}\sin\theta)\sin\theta+(\ddot{r}\sin\theta+2\dot{r}\dot{\theta}\cos\theta-r\dot{\theta}^2\sin\theta+r\ddot{\theta}\cos\theta)\cos\theta\\
=&2\dot{r}\dot{\theta}+r\ddot{\theta}=\frac{1}{r}\frac{d}{dt}(r^2\dot{\theta})
\end{align}
問題
質点ｍが等速円運動をするために必要な向心力の大きさを求めよ。
解答
向心力の大きさを\(f_r\)として\(r\)方向の運動方程式を書くと
\begin{align}
f_r=ma_r=mr\dot{\theta}^2
\end{align}
f_r=ma_r=mr\dot{\theta}^2
\end{align}
\(a_r\)に関しては第1項\(\ddot{r}\)はゼロです。等速円運動なので。
ちなみに\(\dot{\theta}=\omega\)とおくと、これまでに見た公式通りのものがちゃんと導けていることがわかります。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」
スポンサーリンク
東大卒の現役塾講師が
東大理系攻略法を
解説したPDF販売中！
東大理系攻略法を
解説したPDF販売中！
中高一貫校に行かなくても、塾に行かなくても、独学で受かるための勉強法を完全解説！
全科目の参考書
全参考書の使い方
受験までの勉強スケジュール
が全てわかります！
今だけ！100様限定60%OFF！
さらに24時間以内なら返金保証つき！
会員数500万人超の「note」で
無料サンプル公開！
無料サンプル公開！
