極座標表示

記事内に商品プロモーションを含む場合があります
(※数式が見切れている場合は横スクロールしてください。)
これまでよく使われていた\((x,y)\)座標表示を\(r,\theta\)という違う表示の仕方をしていきます。
図を見ていただきます。
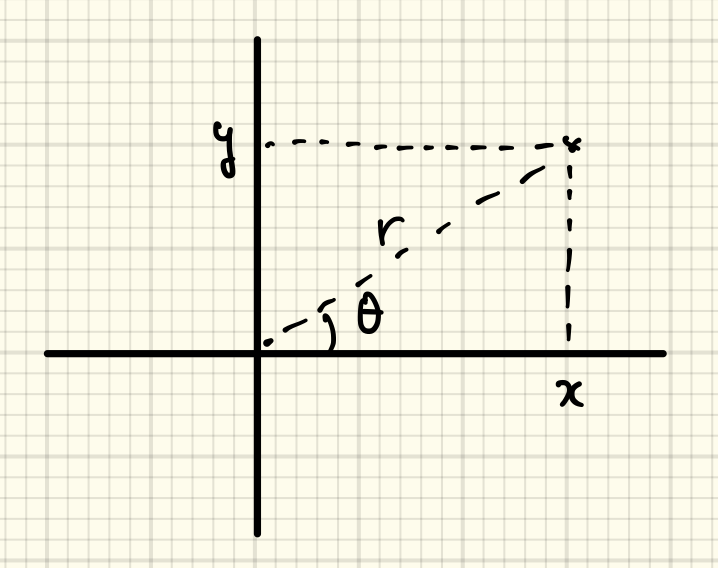
ある位置を指定するためには\((x,y)\)という表示だと
原点から\(x\)軸方向の正の方向に\(x\)だけ進んで、\(y\)軸方向の正の方向に\(y\)だけ進んだところ
という意味で指定します。
これと違う極座標表示だと\((r,\theta)\)を使う時には
原点から距離\(r\)で、始線から角度\(\theta\)のところ
という意味で指定します。先ほどの図だと始線と\(x\)軸の正の部分が一致するように描きました。
この2つの表示の関係性を数式にするなら以下のようになります。
\begin{align}
\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}r\cos\theta\\r\sin\theta\end{pmatrix}
\end{align}
\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}r\cos\theta\\r\sin\theta\end{pmatrix}
\end{align}
問題をいくつか解いて慣れておきましょう。
問題
\(xy\)表示で書かれている以下の座標を極座標表示にせよ。
\begin{align}
&1.\quad\begin{pmatrix}\sqrt{3}\\1\end{pmatrix}\\
&2.\quad\begin{pmatrix}100\\-100\sqrt{3}\end{pmatrix}
\end{align}
&1.\quad\begin{pmatrix}\sqrt{3}\\1\end{pmatrix}\\
&2.\quad\begin{pmatrix}100\\-100\sqrt{3}\end{pmatrix}
\end{align}
解答
1.
最初の問題だけ真面目に解いておきます。
\begin{align}
\begin{pmatrix}\sqrt{3}\\1\end{pmatrix}=&\begin{pmatrix}r\cos\theta\\r\sin\theta\end{pmatrix}
\end{align}
\begin{pmatrix}\sqrt{3}\\1\end{pmatrix}=&\begin{pmatrix}r\cos\theta\\r\sin\theta\end{pmatrix}
\end{align}
結局これは\(r\)と\(\theta\)の連立方程式を解けっていう問題と同じですね。
\begin{align}
&\left(\sqrt{3}\right)^2+1^2=r^2\cos^2\theta+r^2\sin^2\theta\\
\Longleftrightarrow
&4=r^2\\
\Longleftrightarrow
&r=2
\end{align}
&\left(\sqrt{3}\right)^2+1^2=r^2\cos^2\theta+r^2\sin^2\theta\\
\Longleftrightarrow
&4=r^2\\
\Longleftrightarrow
&r=2
\end{align}
ちなみに極座標表示では\(r\)については正の値だけ取ります。
これで\(r\)は決まりましたので、次に\(\theta\)を決めていきます。
\begin{align}
&2\cos\theta=\sqrt{3}\\
\Longleftrightarrow
&\theta=\frac{\pi}{6}
\end{align}
&2\cos\theta=\sqrt{3}\\
\Longleftrightarrow
&\theta=\frac{\pi}{6}
\end{align}
と決まります。
2.
全く同じ解き方で解けてしまうので、答えだけ書くと
\begin{align}
\begin{pmatrix}r\\\theta\end{pmatrix}=\begin{pmatrix}100\\-\frac{\pi}{3}\end{pmatrix}
\end{align}
\begin{pmatrix}r\\\theta\end{pmatrix}=\begin{pmatrix}100\\-\frac{\pi}{3}\end{pmatrix}
\end{align}
となります。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」
スポンサーリンク








