離心率と2次曲線｜ぽこラボ勉強ブログ

(※数式が見切れている場合は横スクロールしてください。)

この節では離心率という概念を新たに導入して、放物線、だ円(円も含む)、双曲線を統一的に考える仕組みを勉強することにします。

早速、例から考えていきましょう。

例

直線l\(y=-p\)と点F\((0,p)\)からの距離が等しい点P\((x,y)\)がある。

ただし\(p>0\)とする。

このような条件を満たす\((x,y)\)をプロットしていった結果、\(x\)と\(y\)はどのような条件式を満たし、どのようなグラフが完成するか考えよ。

※こういう問題を軌跡の問題と言います。

では実際に考えていきます。答えのグラフの形は先にグラフに書き入れましたので、これを参考に考えましょう。

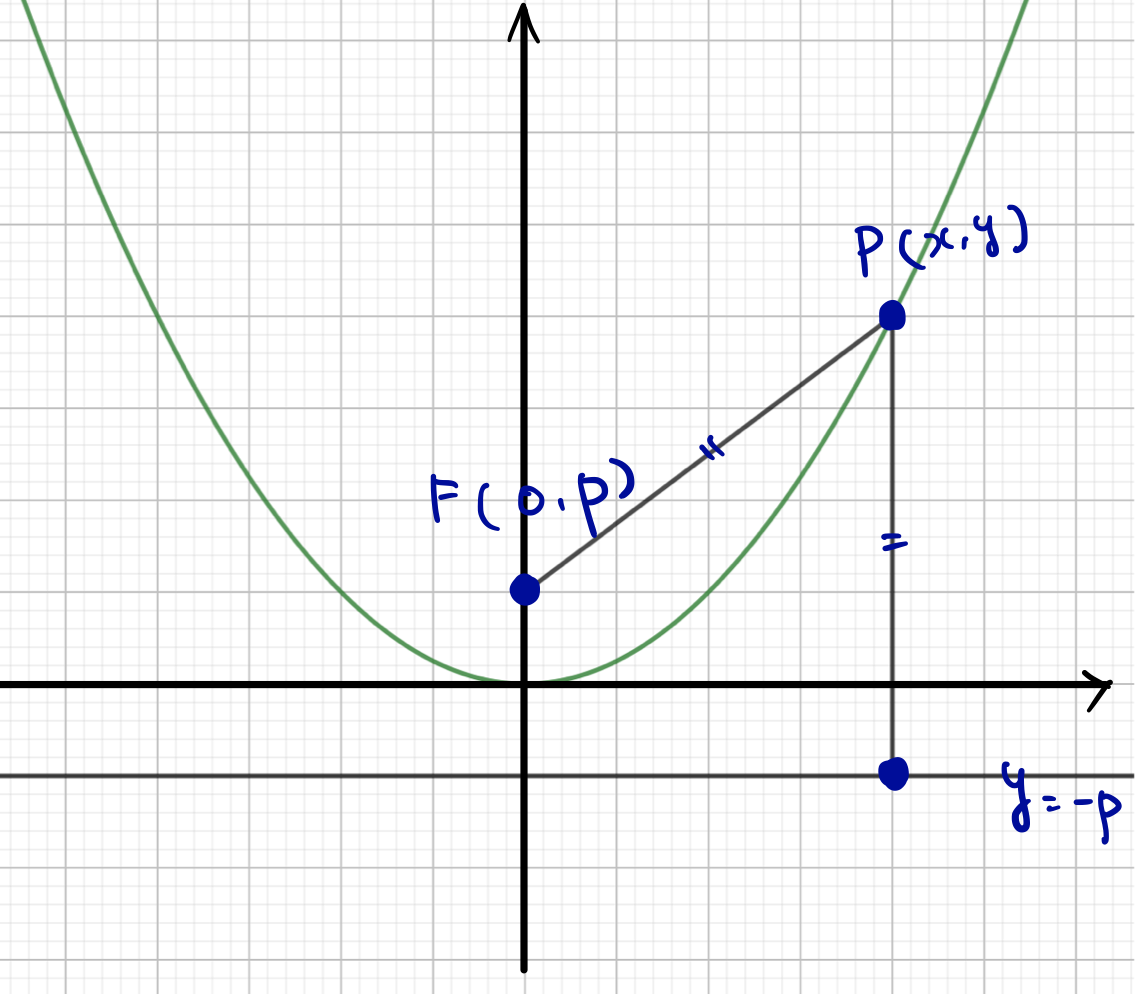
まず、点Pと直線lの距離は\(y+p\)です。

次に点Fと点Pの距離は以下のようになりますね。

\begin{align}
\sqrt{x^2+(y-p)^2}
\end{align}

これらが等しいということから次のように計算を進めることができます。

\begin{align}
&\sqrt{x^2+(y-p)^2}=y+p\\
\Longrightarrow
&x^2+(y-p)^2=(y+p)^2\\
\Longrightarrow
&x^2=4py\\
\Longrightarrow
&y=\frac{1}{4p}x^2
\end{align}

例で与えられた条件を満たす点Pが描く軌跡が放物線になるということがわかりました。

今の例を公式としてまとめておきましょう。

公式

放物線

\begin{align}
y=\frac{1}{4p}x^2
\end{align}

は焦点F\((0,p)\)と準線l\(y=-p\)から距離の等しい点P\((x,y)\)の描く軌跡と表現できる。

この公式を使って問題を1つ解いてみましょう。

問題

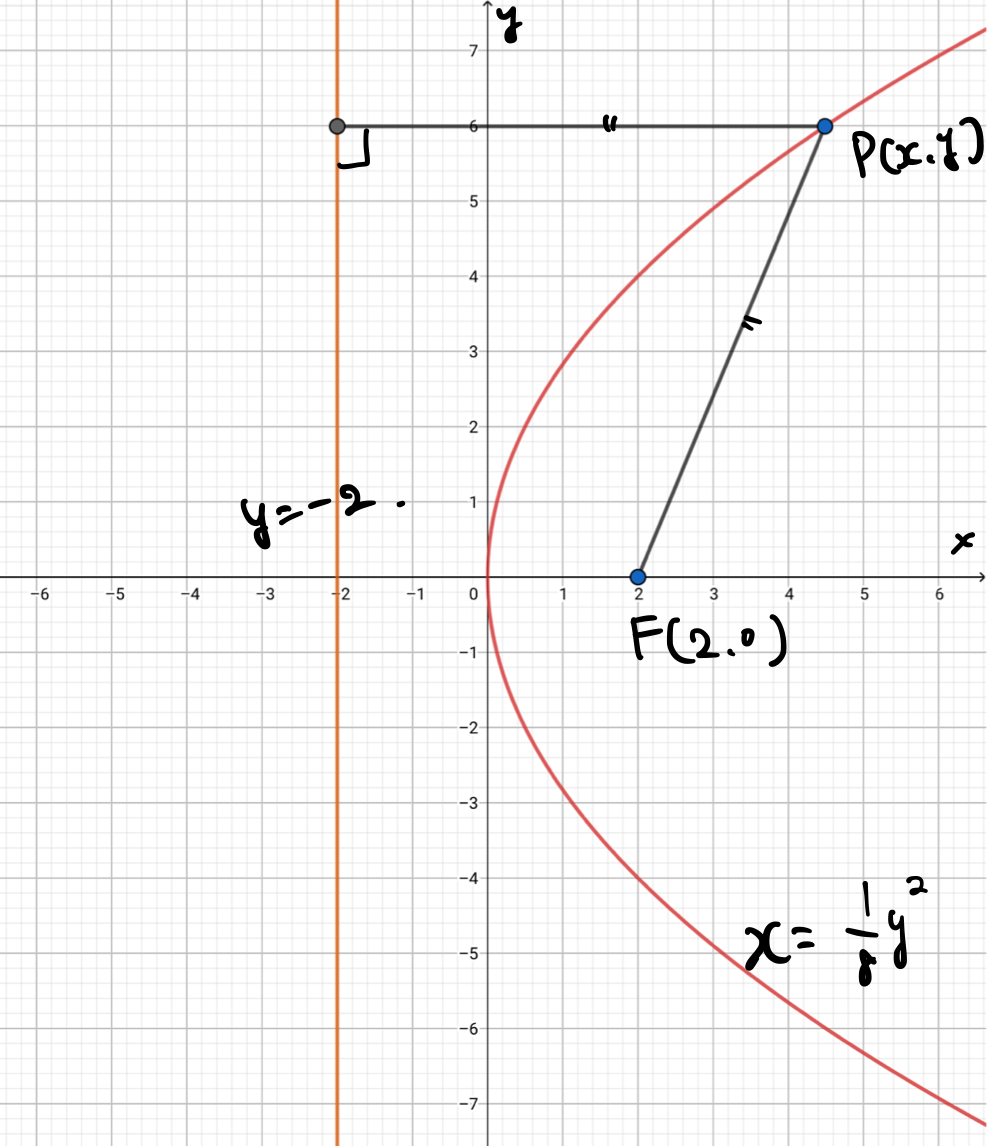
直線\(x=-2\)と点F\((2,0)\)からの距離が等しい点P\((x,y)\)が描く軌跡を求めよ。

解答

公式と比べると準線と焦点の両方とも\(x\)と\(y\)の役割が変わっただけです。

公式だと\(y>0\)方向に開いている放物線を扱いましたが、問題では\(x>0\)方向に開いている放物線を扱うと思えばいいだけです。

実際に計算をすると

\begin{align}
&\sqrt{(x-2)^2+y^2}=x+2\\
\Longrightarrow
&x=\frac{1}{8}y^2
\end{align}

となります。

実は準線lと焦点Fを決めてやって

点Pと準線との距離、点Pと焦点との距離の比を意識してやると実はだ円、放物線、双曲線を統一的に見てやることができます。

これを次に見ていきましょう。

例

焦点F\((c,0)\)、準線l:\(x=-c\)からの距離の比が\(e:1\)となる点P\((x,y)\)が描く軌跡を考えよ。

ただし\(c>0\)とする。

これまでと同じように計算すればいいだけですね。

先に答えを図で見せておきますね。

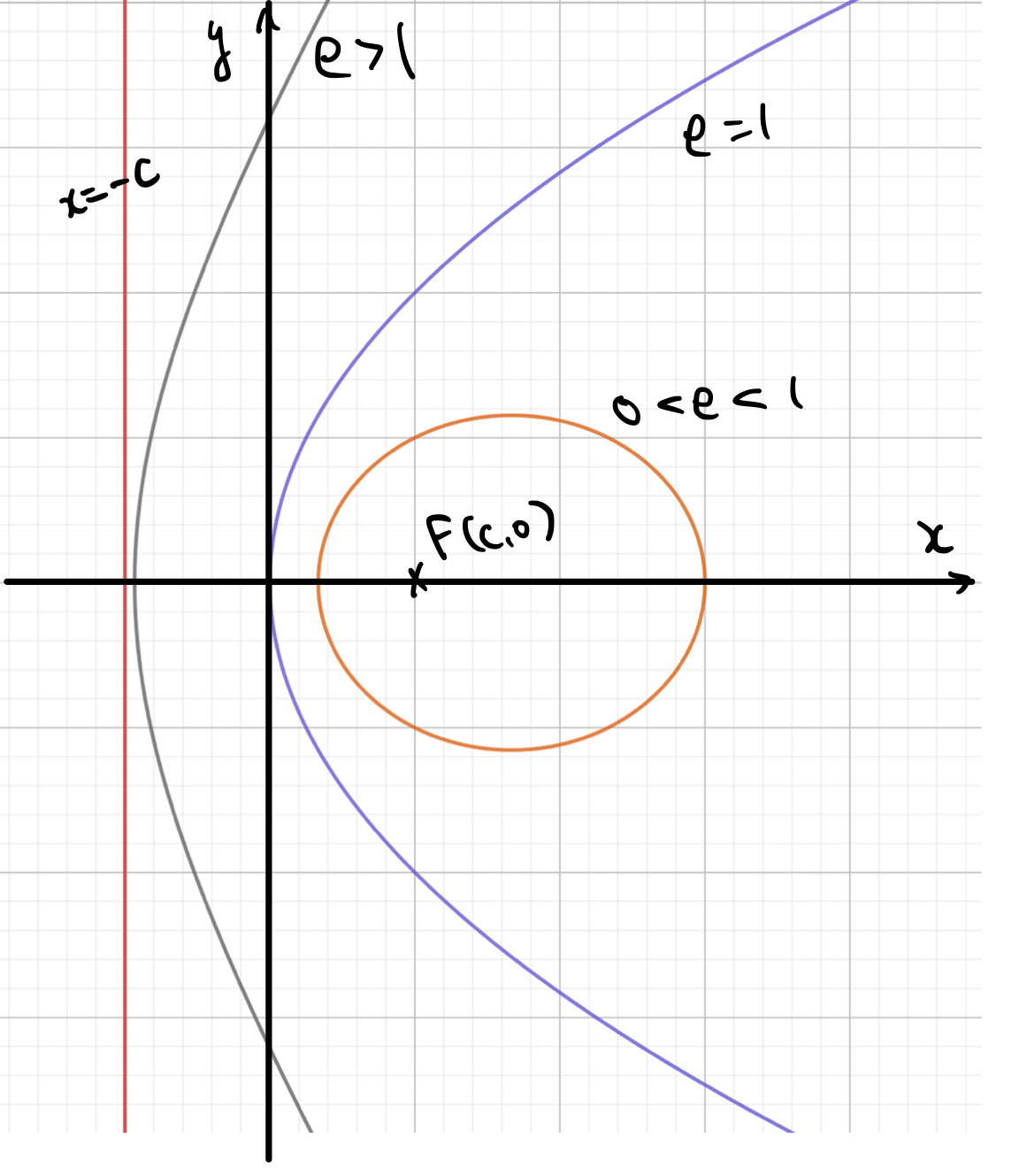
この図を見ながら考えていただけるといいです。

まず焦点との距離は\(\sqrt{(x-c)^2+y^2}\)です。

また点Pと準線lとの距離は\(x+c\)です。

これらの比が\(e:1\)なのですから、以下のような計算ができます。

\begin{align}
&\sqrt{(x-c)^2+y^2}:x+c=e:1\\
\Longleftrightarrow
&e^2(x+c)^2=(x-c)^2+y^2\\
\Longleftrightarrow
&(1-e^2)x^2-2c(1+e^2)x+y^2=(e^2-1)c^2
\end{align}

ここで1つめの場合分けが必要です。\(1-e^2=0\)となるときは放物線が得られますね。

今、長さ同士の比を取っているわけですからもちろん\(e>0\)なので、

\begin{align}
1-e^2=0\Longrightarrow e=1
\end{align}

です。

これを先ほどの式に代入すると、

\begin{align}
-4cx+y^2=0
\end{align}

という放物線ができます。

次に\(e\neq 1\)のときを考えましょう。このときは以下のように計算を進めることができます。ちょっと面倒な平方完成の作業です。

\begin{align}
&(1-e^2)x^2-2c(1+e^2)x+y^2=(e^2-1)c^2\\
\Longleftrightarrow
&x^2-\frac{2c(1+e^2)}{1-e^2}x+\frac{y^2}{1-e^2}=-c^2\\
\Longleftrightarrow
&\left(x-\frac{c(1+e^2)}{1-e^2}\right)^2-\frac{c^2(1+e^2)^2}{(1-e^2)^2}+\frac{y^2}{1-e^2}=-c^2\\
\Longleftrightarrow
&\left(x-\frac{c(1+e^2)}{1-e^2}\right)^2+\frac{y^2}{1-e^2}=c^2\left(\frac{(1+e^2)^2}{(1-e^2)^2}-1\right)\\
\Longleftrightarrow
&\left(x-\frac{c(1+e^2)}{1-e^2}\right)^2+\frac{y^2}{1-e^2}=\left(\frac{2ec}{1-e^2}\right)^2\\
\Longleftrightarrow
&\frac{\left(x-\frac{c(1+e^2)}{1-e^2}\right)^2}{\left(\frac{2ec}{1-e^2}\right)^2}+(1-e^2)\frac{y^2}{(2ec)^2}=1
\end{align}

だいぶ面倒な計算をしましたが、結局、\(1-e^2\)の正負によって左辺の2項目の符号が変わるので、それがだ円と双曲線を分かつ分かれ目になっているということですね。

最終的に、\(0<e<1\)の時はだ円になり、\(e>1\)の時は双曲線になるということがわかります。

改めて先ほどの答えの図を描いてみると、

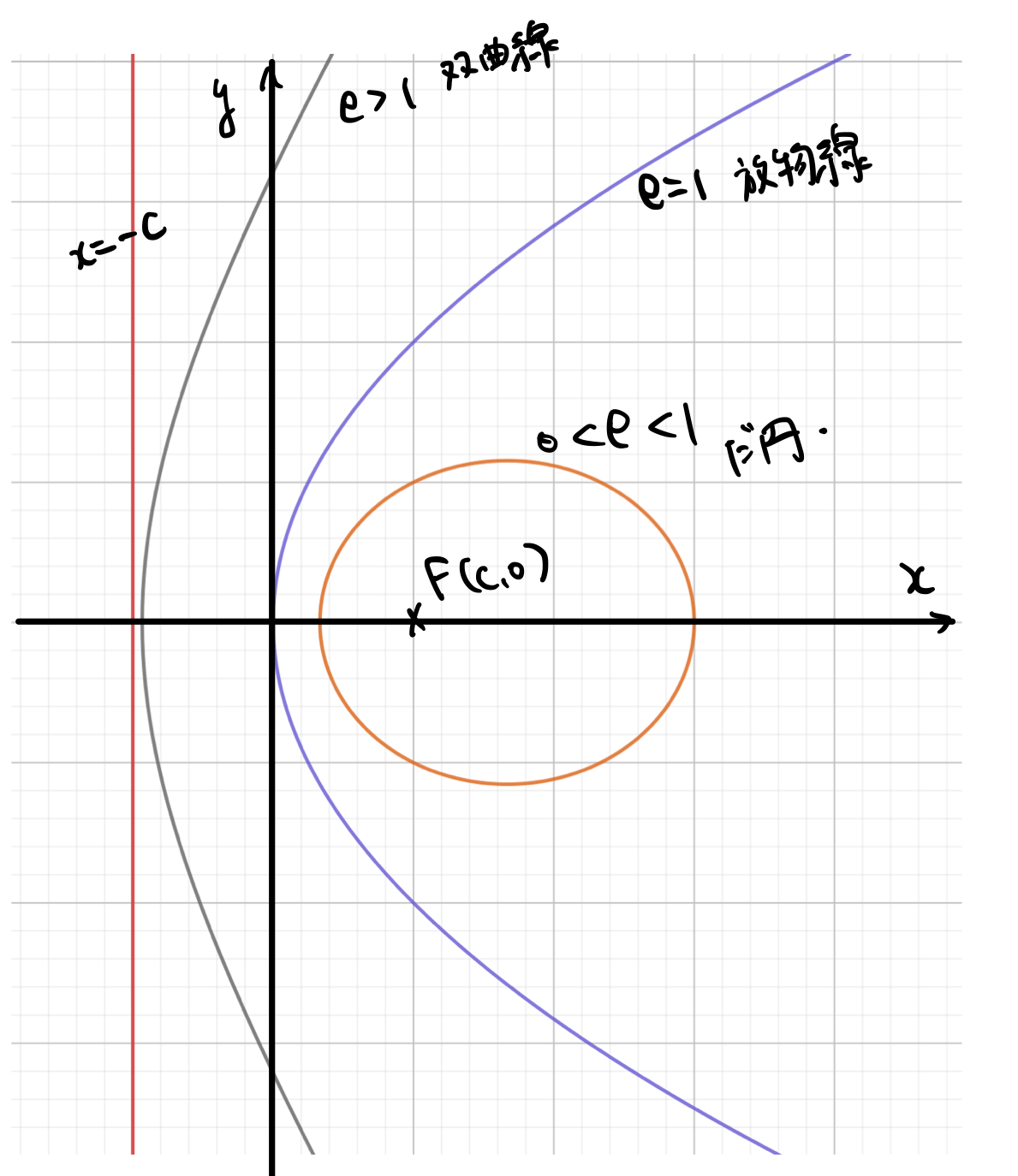
となりますね。ちなみに\(e\)の大小というのは点Pが準線に近いのかそれとも、焦点に近いのかというのを表すものです。

\(0<e<1\)というのは点Pが常に準線よりも焦点に近いので、焦点をぐるっと回ってくれて、逆のときには焦点を回るようなことにはならないということです。

こういった直感的な理解もすごく重要です。

最後にこの後で勉強するケプラーの法則の準備として、焦点が原点に来る場合について少しだけコメントしておきます。

焦点が原点に来るような2次曲線を考えたかったら、ここまでに考えてきたものをまるまる全て\(x\)軸のマイナス方向に\(c\)だけ動かせばいいです。

それは結局\(x\to x+c\)という変換をしているに過ぎないですね。

そうすると最終的な結果としては

離心率\(e\)が\(1\)のときには

\begin{align}
-4c(x+c)+y^2=0
\end{align}

の放物線になりますし、\(e\neq1\)のときには

\begin{align}
\frac{\left(x+c-\frac{c(1+e^2)}{1-e^2}\right)^2}{\left(\frac{2ec}{1-e^2}\right)^2}+(1-e^2)\frac{y^2}{(2ec)^2}=1\\
\Longleftrightarrow
\frac{\left(x-\frac{2ce^2}{1-e^2}\right)^2}{\left(\frac{2ec}{1-e^2}\right)^2}+(1-e^2)\frac{y^2}{(2ec)^2}=1
\end{align}

となります。

関連リンク

>>ブログ版アラサー高校物理の記事一覧

>>物理の勉強ロードマップ【2019年版】

>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」