(※数式が見切れている場合は横スクロールしてください。)
さてマキノさん、この節では「相対」という単語のくっついた位置、速度、加速度について考えます。後々ちゃんと勉強するのですが、結構難しいので、簡単なところに絞ったものから解説していくことにしますね。
さっきまでとは少しだけ毛色が変わるんですけど、そこはすいません。。。
ここでも簡単のために1次元上の運動を考えることにします。今回はより細かくして、固定された数直線上の動きを考えることにしましょう。数直線には原点があり、正負の両方向に無限に伸びています。
最初に相対位置について勉強しましょう。
Aさんが数直線上の\(＋5\)kmの地点にいるとします。Bさんは数直線上の\(＋10\)kmの地点にいるとします。
ここで、\(＋5\)kmとか\(＋10\)kmとかいうのは、原点から見たAさんとBさんの位置です。
ところが、Aさんから見ればBさんは「自分よりも＋方向に\(5\)km進んだところにいます」し、Bさんから見れば、Aさんは「自分よりもー方向に\(5\)km進んだところにいます」。
この「自分よりも」のところが原点以外にある場合、その位置を相対位置と言います。（最初のAさんBさんの位置も原点から見た相対位置と言えるのですけどね。。。）
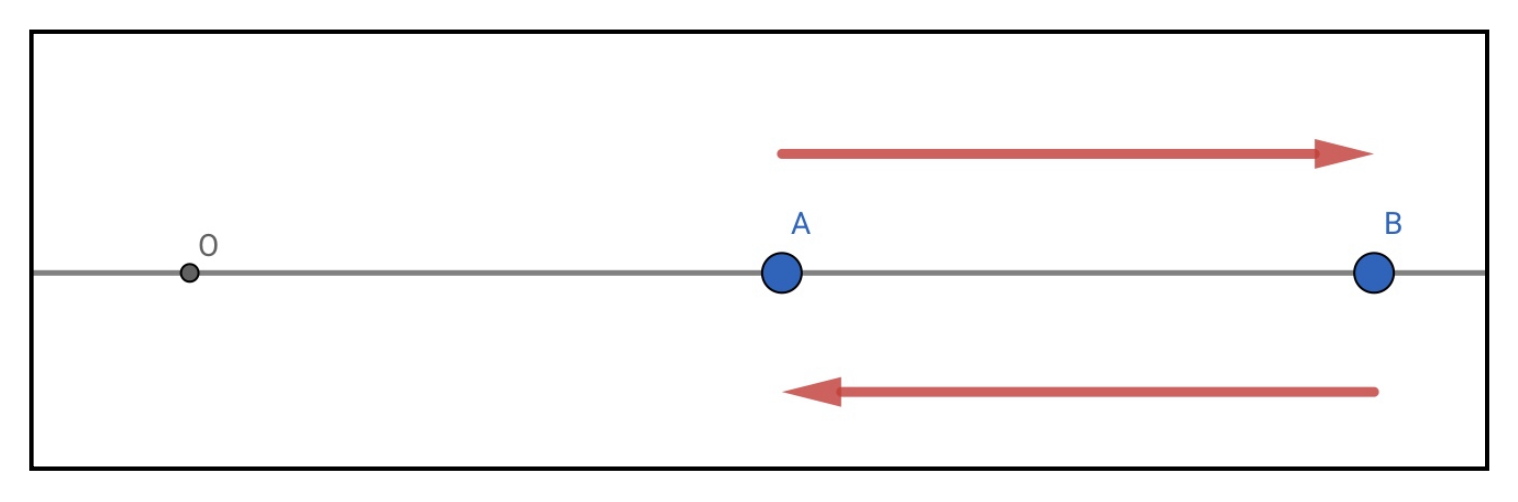
Aさんから見たBさんの相対位置は？と聞かれたら、\(+5\)kmと答えれば良いですし、
Bさんから見たAさんの相対位置は？と聞かれたら、\(-5\)kmと答えれば良いです。
より一般的にAさんの原点からの位置が\(+a\)、Bさんの原点からの位置が\(+b\)の時には、
Aさんから見たBさんの相対位置は\((b-a)\)、Bさんから見たAさんの相対位置は\((a-b)\)となります。
相対位置を計算したければ
（相手の値）マイナス（自分の値）
\end{align}
をすれば良いと覚えておくといいでしょう。
次は相対速度について考えてみましょう。
同じ数直線上を今度はAさんはとぼとぼと時速\(6\)km（等速）で正の方向へと歩いています。Bさんは時速\(9\)km（等速）で正の方向へ向けてジョギングしています。
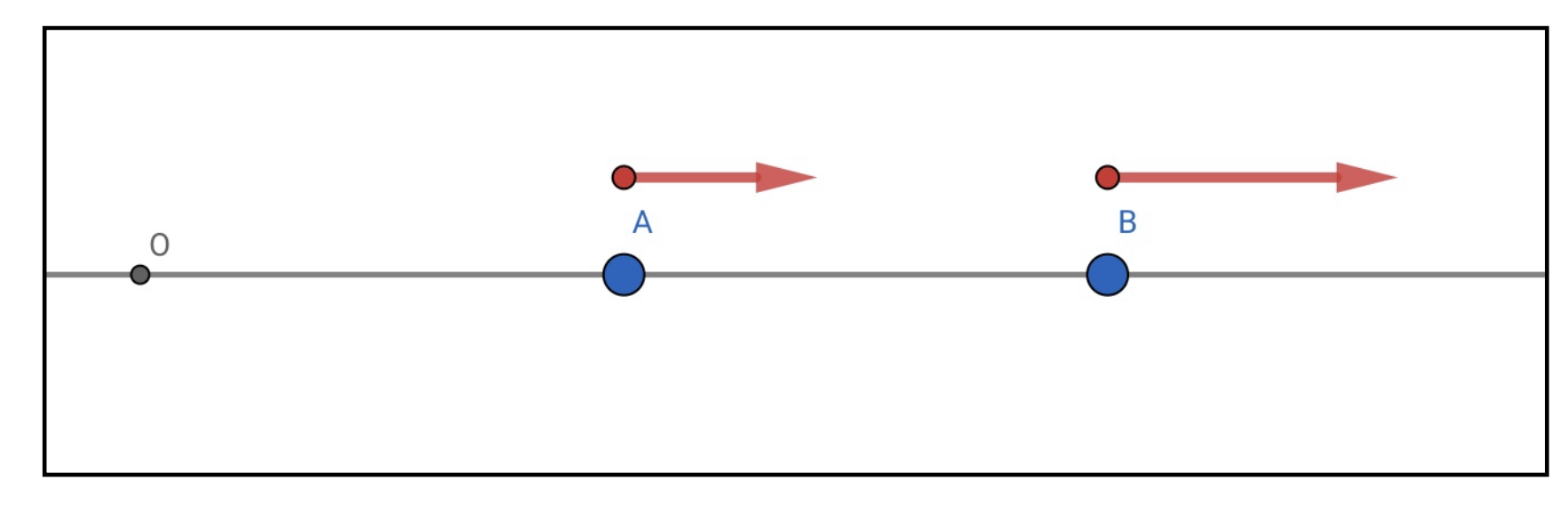
このとき、Aさんから見たら、Bさんは時速\(3\)kmで正の方向へと進んでいるように見えます。
逆にBさんから見るとAさんは時速\(3\)kmで負の方向へ進んでいるように見えます。
相対速度も相対位置と概念的にはほとんど同じように考えれば良いです。
イメージが難しかったら、高速道路なんかで、追い抜いたり追い抜かれたりするのをイメージしてください。同じ方向にかなりの速さで進んでいるのに、横の車がゆっくり前に進んでいるように見えたり、逆に横の車がゆっくり後ろに進んでいるように見えたりすることがありますよね。
その速度のことを相対速度と言います。
今回の場合は、
Aさんから見たBさんの相対速度は？と聞かれたら、\(+3\)km/hと答えれば良いですし、
Bさんから見たAさんの相対速度は？と聞かれたら、\(-3\)km/hと答えれば良いです。
より一般に、Aさんは時速\(6\)kmではなく\(a\)km/hで数直線上の正の方向に進んでいて、Bさんは\(b\)km/hで数直線上の正の方向に進んでいるとすると、
Aさんから見たBさんの相対速度\((b-a)\)km/h ですし、Bさんから見たAさんの相対速度は\((a-b)\)km/hです。
ここでもやはり「相手の値」マイナス「自分の値」というルールが使えます。
ちなみに\(a\)とか\(b\)とかがマイナスの値でも同じように計算できます。数直線上を負の方向に進んでいる場合は、正の方向にマイナスの速度で進んでいると考えて計算すれば良いわけです。
最後に相対加速度ですね。
今度はAさんが毎時\(2\)km/hずつ正の方向に加速していて、Bさんが毎時\(4\)km/hで正の方向に加速しているとしましょう。
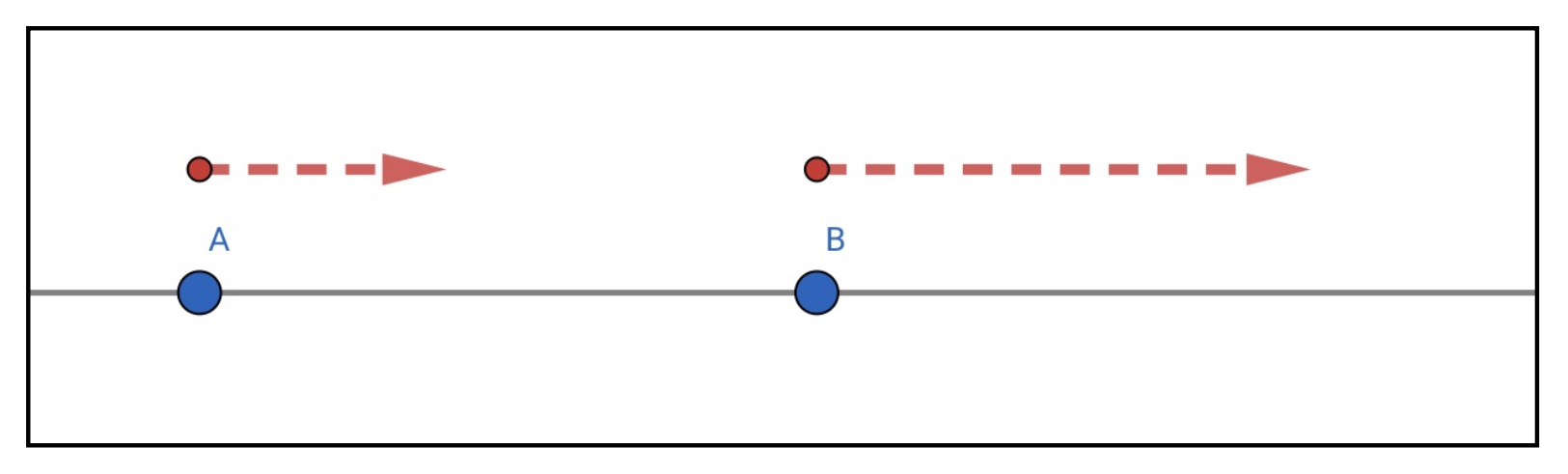
やはり考え方は同じで、
Aさんから見ればBさんは毎時\(+2\)km/h加速しているように見えるし、Bさんから見ればAさんは毎時\(-2\)km/h加速しているように見えます。
こういった値のことを相対加速度と言います。
同じスピードで同じ方向に走っている2台の車を考えて、その車のアクセルの踏み具合によって、隣の車がだんだん早くなっているように見えたり、遅くなっているように見えたりするのは、相対加速度によるものです。
より一般的にAの加速度が\(a\)で、Bの加速度が\(b\)なら、
Aから見たBの相対加速度は\((b-a)\)で、Bから見たAの相対加速度は\((a-b)\)です。
それでは次の問題を解いて少し慣れてもらうことにしましょう。
問題
質点mと質点Mが同一数直線上を運動している。
mの加速度と、初期速度、初期位置は以下のようになっていることがわかっている。
&a_m(t)=0\\
&v_m(t=0)=1,\quad x_m(t=0)=0
\end{align}
同じくMについては以下のことがわかっている。
&a_M(t)=2\\
&v_M(t=0)=-1,\quad x_M(t=0)=-1
\end{align}
このときに\(t≧0\)のmから見たとMの相対加速度、相対速度、相対位置をそれぞれ求めよ。
解答
まずは積分して、それぞれ速度と位置の関数を得ることにしましょう。まずmについては以下のようになります。
&v_m(t)=v_m(t=0)+\int^t_00dt=1\\
&x_m(t)=x_m(t=0)+\int^t_10dt=t
\end{align}
続いてMについては以下のようになります。
&v_m(t)=v_m(t=0)+\int^t_02dt=-1+2t\\
&x_m(t)=x_m(t=0)+\int^t_1(-1+2t)dt=-1-t+t^2
\end{align}
これらを引き算すればいいわけですね。
求めるのはmから見たMの相対加速度、相対速度、相対位置なので、
&a(t)=2-0=2\\
&v(t)=-1+2t-1=-2+2t\\
&x(t)=-1-t+t^2-t=-1-2t+t^2
\end{align}
となります。
次は1次元の運動から抜け出すための数学的準備です。ここからが本番ですよ。マキノさん、がんばりましょう。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」
東大理系攻略法を
解説したPDF販売中！
中高一貫校に行かなくても、塾に行かなくても、独学で受かるための勉強法を完全解説！
全科目の参考書
全参考書の使い方
受験までの勉強スケジュール
が全てわかります！
今だけ！100様限定60%OFF！
さらに24時間以内なら返金保証つき！
無料サンプル公開！
