(※数式が見切れている場合は横スクロールしてください。)
今回は少し話が変わって動く座標系です。
ここまでで座標系という話はしていませんでした。
そもそも静止している場所から何かしらの物体の運動を見るということ自体はかなり難しいです。
普通に床の上で箱を滑らせるなんてことを考えても、地球は自転も公転もしていますから、自分は動いている座標系で運動を眺めているわけです。
というわけで座標系が動いているときには具体的にはどんなことが起こるか学習していきましょう。
まず直交座標系\((x,y)\)と\((x’,y’)\)の2つを準備します。
このうち\((x’,y’)\)は\(\vec{V}\)で動いているとしましょう。
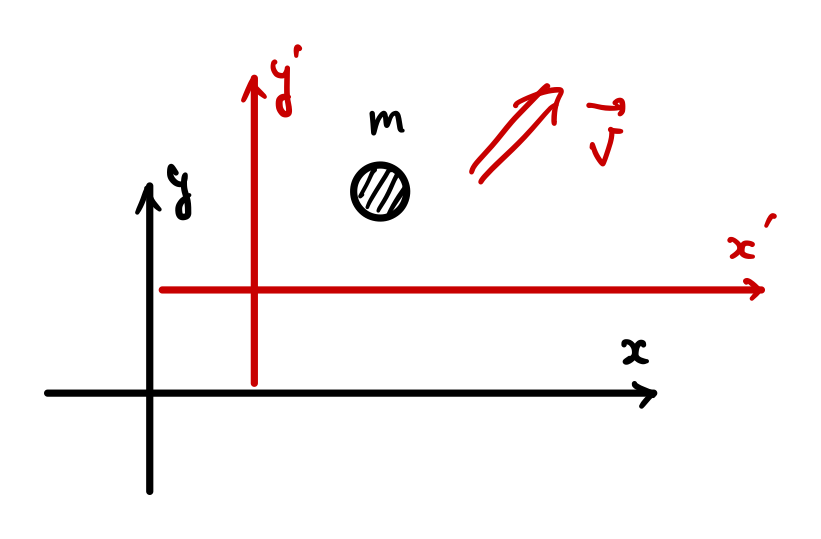
この2つの座標系で、質点mの運動を眺めてみましょう。
質点mの運動はどのような座標でも同じになるはずです。座標系というのはもちろん人間が恣意的に決めているわけですから運動自体は同じです。
さて、静止座標系の\((x,y)\)系で見たときに、質点ｍにかかる力が\(\vec{F}\)だとすると、この座標系の運動方程式は以下のようになります。
\vec{F}=m\dot{\vec{v}}
\end{align}
相対速度を考慮すると、\((x’,y’)\)系で見たときの速度\(\vec{v’}\)は以下のようになります。
\vec{v’}=\vec{v}-\vec{V}
\end{align}
\((x’,y’)\)系で見たときの運動方程式は次のようになります。
\vec{F’}=&m\dot{\vec{v’}}\\
=&m(\dot{\vec{v}}-\dot{\vec{V}})\\
=&\vec{F}-m\dot{\vec{V}}
\end{align}
座標系によって\(-m\dot{\vec{V}}\)の見かけの力が働きます。これを慣性力と言います。
ポイントはどの座標系で見ても同じ運動方程式の形が使えるということです。
これだけだとイマイチ分からないと思うのですが、ひとまず慣れるのがメインだと思っていくつか例を見ていただくのがよろしいかと思います。
例
等加速度で\(x\)方向に運動している電車内に吊るしている質点ｍを2つの座標系で見てみることにしてみましょう。
上は地面に固定されている座標系\(x\)系で見ていて、質点mは電車と同じ加速度\(a\)で運動しています。
下は電車に固定された座標系\(x’\)系で見ていて、質点ｍは静止しています。
\(x\)系で見たとき、質点mの\(x\)方向の運動方程式と、鉛直方向のつり合いを記述すると以下のようになります。
&T\sin\theta=ma\\
&T\cos\theta=mg
\end{align}
となります。
次に\(x’\)系で見たとき、質点ｍの\(x’\)方向のつり合いと、鉛直方向のつり合いを記述すると以下のようになります。
&T\sin\theta=ma\\
&T\cos\theta=mg
\end{align}
結局、同じ式になるんです。ただ、つり合いの式と理解するのか、運動方程式と理解するのか、という理解の仕方が系によって変わってくるということを知っておくといいですね。
ちなみに\(x’\)系で見ると、重力加速度が角度\(\theta\)の方向に\(g’=\sqrt{g^2+a^2}\)の強さでかかっていると見ることもできます。
次の例を見てみましょう。
例
平面上で等速円運動をしている質点ｍの状態を2種類の系で考えよ。
1つは円運動を外から見る系、1つは質点ｍに固定されていて、質点ｍと一緒に動く系で考えよ。
外から運動を見るときには、向心力が働いていて、円運動の加速度はその向心力から得ているという、運動方程式で質点ｍの運動を記述できます。
f=mr\omega^2
\end{align}
次に、質点に固定された系で見ると、質点は静止しています。ですから、力のつり合いの式を使って質点を表現できます。
f=mr\omega^2
\end{align}
この右辺に関しては、慣性力の1つで遠心力と言います。遠心力という言葉自体は慣れていらっしゃると思いますが、それが慣性力の1つで、どの系で見るかによって出てくるものであるということを意識していることはないのではないかと思います。
その遠心力という考え方を使って問題を解いてみましょう。
問題
以下の図のように、横にして固定した円柱を質点が滑り落ちていく様子を考える。
円柱の頂点から滑り始めて、質点が円柱から離れる角度はいくらかを計算せよ。
解答
遠心力という考え方を持ってくるためには、滑り落ちている質点の上に乗っている系で物理を見ないといけません。
質点に乗っている系で質点の運動方程式を記述すると以下のようになります。
mg\cos\theta=N+m\frac{v^2}{r}
\end{align}
これ以上に考えを進めるには角度\(\theta\)のときに、速度\(v\)がどれくらいなのか知る必要があります。
これはエネルギー保存則でいけます。
&mg\cdot 2r=mgr(1+\cos\theta)+\frac{1}{mv^2}\\
\Longleftrightarrow
&mv^2=2mgr(1-\cos\theta)
\end{align}
これを運動方程式に代入すると、垂直抗力\(N\)を求めることができます。
N=-2mg+3mg\cos\theta
\end{align}
これが\(0\)になる瞬間が質点が円柱から離れる瞬間です。そうなる\(\theta\)は\(\cos\)で表現すると以下のようになります。
\cos\theta=\frac{2}{3}
\end{align}
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」
東大理系攻略法を
解説したPDF販売中！
中高一貫校に行かなくても、塾に行かなくても、独学で受かるための勉強法を完全解説！
全科目の参考書
全参考書の使い方
受験までの勉強スケジュール
が全てわかります！
今だけ！100様限定60%OFF！
さらに24時間以内なら返金保証つき！
無料サンプル公開！
