角運動量

(※数式が見切れている場合は横スクロールしてください。)
ここでは角運動量という新しい量を導入します。力学でももちろん重要な量ですし、ずっと先に量子力学を勉強するときにはさらに重要な役割を果たす量です。本来、高校の範囲で取り上げられることはないのですが、しっかり勉強しておきましょう。
この章よりも以前に「運動量」という量を扱いました。何度も登場したのは質点の運動量で、質点の運動量というのは質点の持つ勢いみたいなものとお話しました。衝突や合体、分離というときに出てくる量でしたね。
今回は角運動量というものです。運動量とは全く概念が異なりますので、言葉と定義をしっかりおさえておきましょう。
まず質点mが\(xy\)平面上で等速円運動をしている状況を考えましょう。角運動量は3次元でないと定義できないので、最初から質点の位置は以下のように3次元で表示することにします。
\vec{x}(t)=\begin{pmatrix}r\cos\omega t\\ r\sin \omega t\\0\end{pmatrix}
\end{align}
これが質点mの位置ベクトルです。原点を中心に半径の円を速さで反時計回りに運動していることがこの形からわかります。わからない場合は円運動の章を見返してください。
さてこの質点mの運動量\(\vec{p}(t)\)は以下のように計算できます。
\vec{p}(t)=m\dot{\vec{x}}(t)=m\begin{pmatrix}-r\omega\sin\omega t\\ r\omega\cos \omega t\\0\end{pmatrix}
\end{align}
この位置ベクトルと運動量の外積を角運動量と定義します。ただし、今回は原点からの変位で位置ベクトルを定義しているので、原点回りの角運動量と呼びます。原点回りの角運動量は、
\vec{L}(t)=\vec{x}(t)\times\vec{p}(t)=\begin{pmatrix}0\\0\\mr^2\omega\end{pmatrix}
\end{align}
となります。外積の計算は少し前の問題と全く同じなので省略しました。等速円運動だと円の中心回りの角運動量は時間によらず一定となります。
角運動量はベクトル量なので、向きと大きさがそれぞれ重要な意味を持ちます。図を見ながら理解していきましょう。
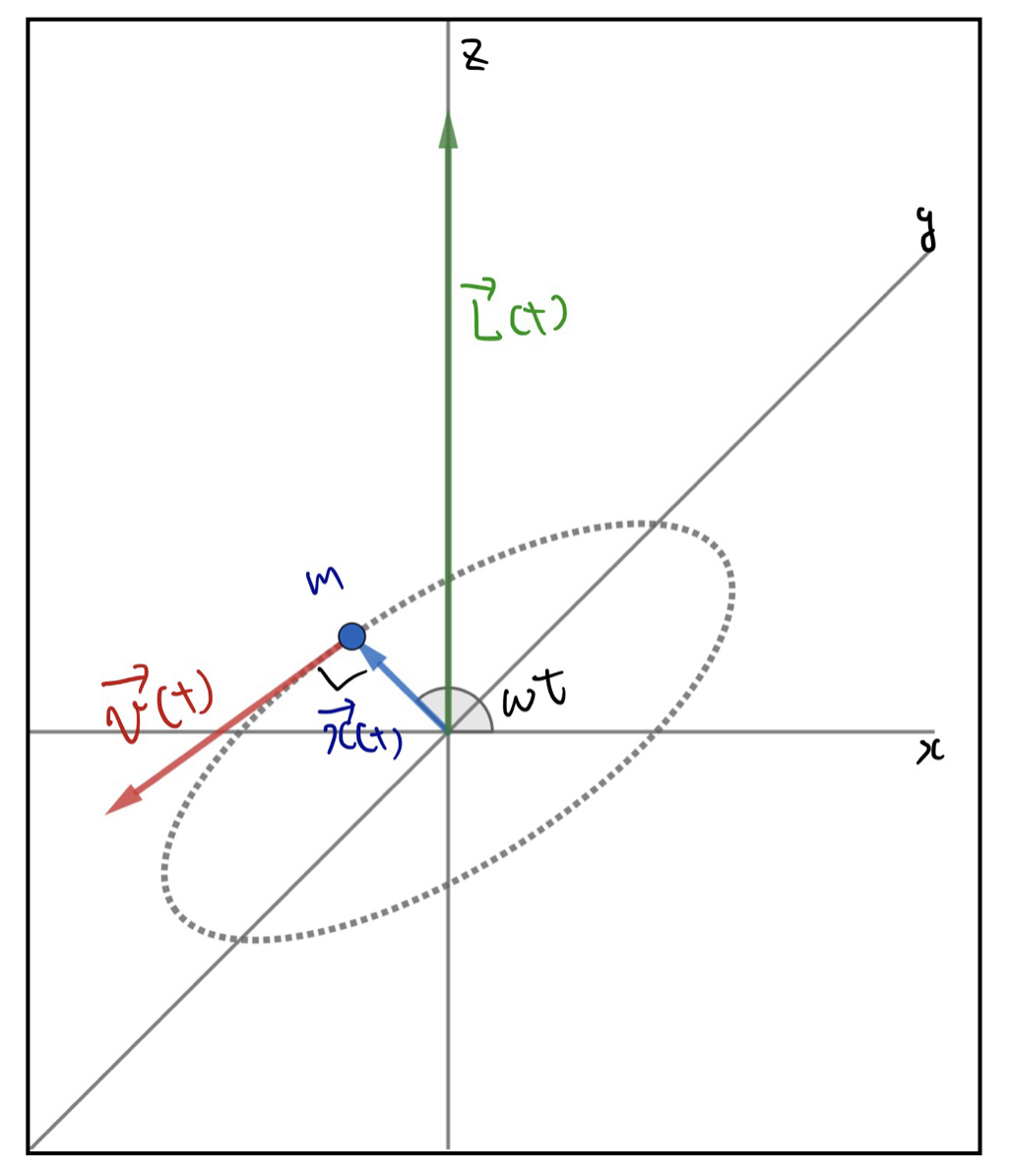
まず、質点の運動を右ねじを回す向きだと思うことにすると、角運動量は右ねじの進む向きを表しています。逆に言えば、角運動量の向きから質点の回転の方向を特定することもできるわけですから、角運動量の向きは回転の向きを示す指標になっています。
そして等速円運動の場合は、先ほど計算した通り、角運動量の大きさは
\left|\vec{L}(t)\right|=mr^2\omega
\end{align}
となります。円運動の節で等速でない場合の円運動を1つ扱いましたが、そこでは円が大きくなるに従って初速が大きくないとうまく回転しないことを見ました。半径が大きくなるほど回転の勢いが必要であることは想像できますし、また角速度に関して言えば、それこそ正に回転の勢いを示すものです。
よって、大雑把には角運動量の大きさは回転の勢いを表す指標だと考えておいてください。今の段階ではここまで分かっておけば十分です。運動量のときにも始めて勉強した場合には、時間をかけてその表す意味を少しずつ吸収していったはずですが、角運動量についてもやはり同じことが言えて、少しずつその量の表す意味を吸収していく他ありません。
ちなみにこの角運動量あたりから一気に計算ができなくなる大学生なんかは割と増えますので、注意が必要なのですが、このテキストでは角運動量も他の量と同じ温度で解説し、特別扱いしないので、ここまで付いて来られたマキノさんなら大丈夫でしょう。
では角運動量についてまとめておきます。
定義
質点mの点P回りの角運動量\(\vec{L}(t)\)は、質点の点Pからの変位を表す位置ベクトル\(\vec{x}(t)\)と、その運動量ベクトル\(\vec{p}(t)\)を用いて以下のように定義する。
\vec{L}(t)=\vec{x}(t)\times\vec{p}(t)
\end{align}
この角運動量の向きは質点mの点P回りの回転の方向を示す指標として、角運動量の大きさは回転の勢いを示す指標として考えることができる。
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」







