(※数式が見切れている場合は横スクロールしてください。)
ベクトルは定数倍だけでなく足し算（合成ともいう）することができます。まずは以下の図からベクトルの足し算のイメージを理解していただきたいです。
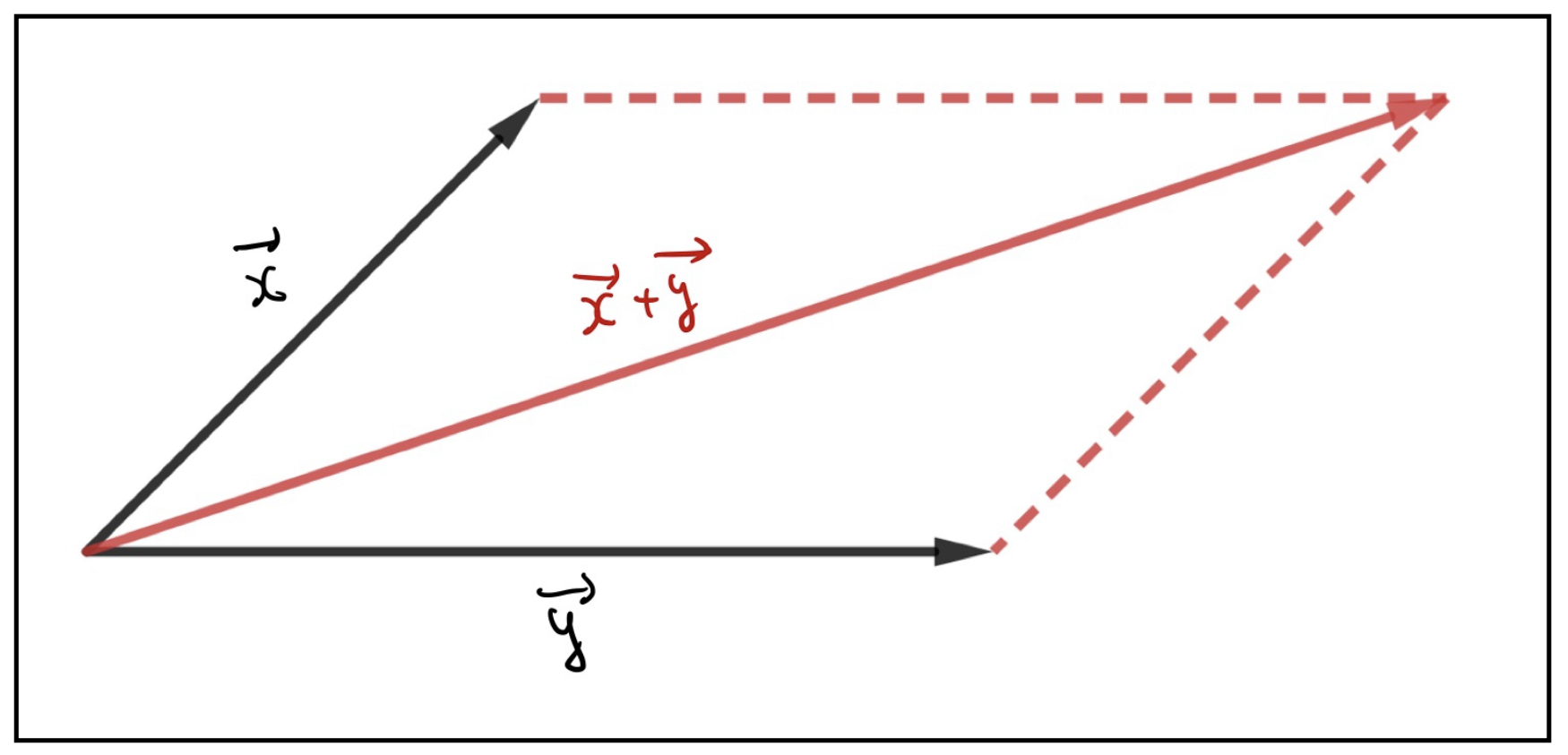
このように2つのベクトルの足し算は、もとのベクトル2つを元によって作られる平行四辺形の、対角線に対応します。
もし、元となる2つのベクトルの始点が揃っていない場合には平行移動して、始点を揃えてから足し算すれば良いだけです。
場合によっては以下のように1つのベクトルの平行移動を用いて、片方の終点ともう片方の始点を揃えるようにすると、全く同じベクトルの足し算をしたことになります。
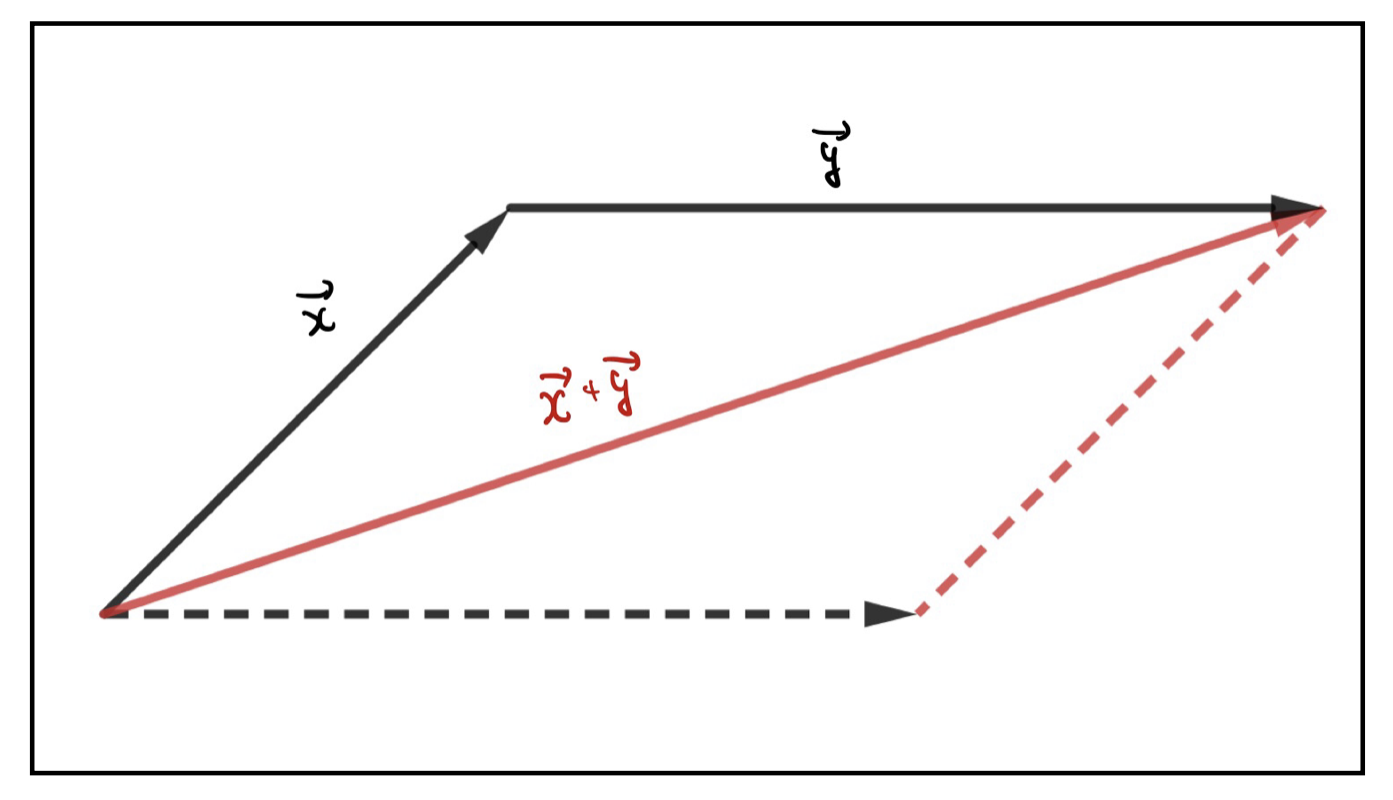
この場合だと\(\vec{y}\)の始点と\(\vec{x}\)の終点を合わせるように\(\vec{y}\)を平行移動させたことになります。
平行移動によって始点同士を合わせる方法も、終点と始点を合わせる方法も両方ともできるようになっておくと便利ですね。
3つ以上のベクトルを足し算する場合には後者の方法の方が見た目にはイメージしやすいことが多いと思います。要するに1つのベクトルの終点と2つ目のベクトルの始点を合わせて、次に2つ目のベクトルの終点と、3つ目のベクトルの始点を合わせて、最終的に1つ目のベクトルの始点から3つ目のベクトルの終点へ引いた矢印が3つのベクトルの合成した結果です。
問題を解いて、ベクトルの合成に慣れていただきましょう。
問題
以下のような正六角形ABCDEF上に2つのベクトルを準備する。
\vec{AB}=\vec{x},\quad\vec{AF}=\vec{y}
\end{align}
この2つのベクトルを用いて、以下のベクトルを表現せよ。
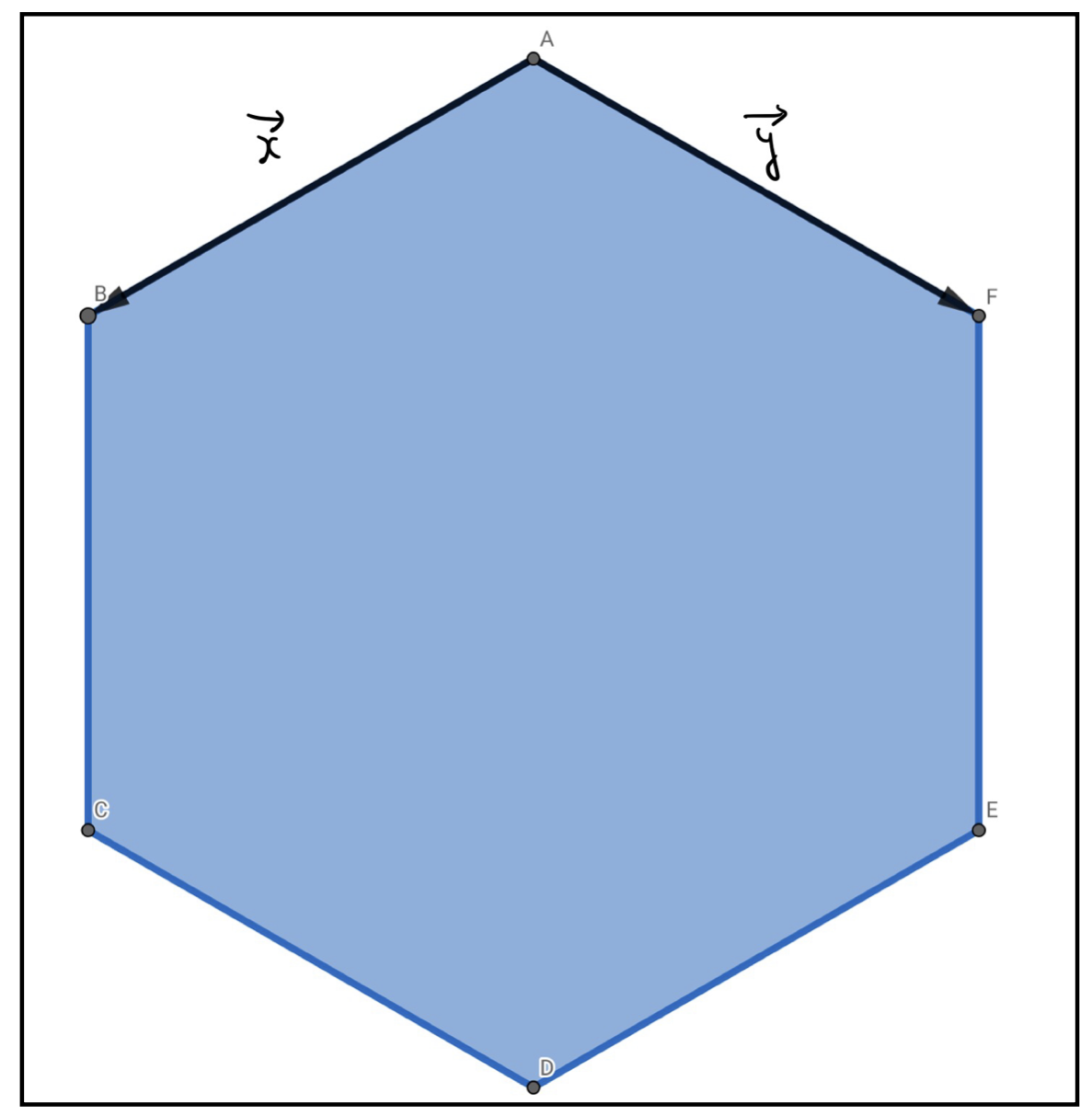
&1.\quad\vec{BC}\qquad2.\quad\vec{AC}\qquad3.\quad\vec{AE}\\
&4.\quad\vec{AD}\qquad5.\quad\vec{CE}
\end{align}
解答
1.
正六角形のど真ん中を点Oとします。すると図形の性質から、
\vec{BC}=\vec{AO}
\end{align}
がわかります。また点Oは平行四辺形ABOFの頂点としてみることができるので、
\vec{BC}=\vec{AO}=\vec{x}+\vec{y}
\end{align}
2.
ベクトルの足し算の性質からすぐに計算できて、
\vec{AC}=&\vec{AB}+\vec{BC}\\
=&\vec{x}+\left(\vec{x}+\vec{y}\right)\\
=&2\vec{x}+\vec{y}
\end{align}
3.
AからEに行くには、Fを経由していく以下のような足し算を考えればいいです。（\(\vec{FE}\)と\(\vec{BC}\)が同じであることに注目すれば解ます。）
\vec{AE}=&\vec{AF}+\vec{FE}\\
=&\vec{AF}+\vec{BC}\\
=&\vec{y}+\left(\vec{x}+\vec{y}\right)\\
=&\vec{x}+2\vec{y}
\end{align}
4.
\vec{AD}=&\vec{AC}+\vec{CD}\\
=&2\vec{x}+\vec{y}+\vec{y}\\
=&2\vec{x}+2\vec{y}
\end{align}
5.
\(\vec{AE}\)は以下のように書けます。
\vec{AE}=\vec{AC}+\vec{CE}
\end{align}
これを変形して\(\vec{CE}\)は
\vec{CE}=&\vec{AE}-\vec{AC}\\
=&\vec{x}+2\vec{y}-\left(2\vec{x}+\vec{y}\right)\\
=&-\vec{x}+\vec{y}
\end{align}
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」
東大理系攻略法を
解説したPDF販売中！
中高一貫校に行かなくても、塾に行かなくても、独学で受かるための勉強法を完全解説！
全科目の参考書
全参考書の使い方
受験までの勉強スケジュール
が全てわかります！
今だけ！100様限定60%OFF！
さらに24時間以内なら返金保証つき！
無料サンプル公開！
