(※数式が見切れている場合は横スクロールしてください。)
前の力学の章では、運動方程式の両辺を時間積分することで、運動量と力積の関係が得られることを見てきました。
今度は時間積分ではなく、空間の成分で積分をするとどのような知識が得られるのかを見ることにしますね。
今回も簡単のために一度、1次元上の運動だけを考えることにします。後の章で数学準備を挟んで、3次元でも通用する形に拡張しますので、お楽しみに。
それでは早速考えていきましょう。設定はいつも通りです。
1次元上（直線上）を運動している質点mの運動を考えます。
質点mには力Fが加えられているとすると、運動方程式は以下の形になります。
m\dot{v}(t)=F(t)
\end{align}
1次元上なので、ベクトルではなくスカラーで書いています。また加速度は速度の時間微分で書いたほうがあとあと楽なので、そのように書いています。
この運動方程式の両辺を空間で（すなわち\(x\)で）積分することにしましょう。すると以下のような形になります。
m\int^{x_2}_{x_1}\dot{v}(t)dx=\int^{x_2}_{x_1}F(t)dx
\end{align}
このままではどのように計算を進めていいかわかりませんよね。ここで（わざわざ長々と準備してきた）置換積分のテクニックを使って積分変数をからに取り替えてみましょう。
そのためにはまず、対応する積分範囲ですが、
\begin{cases}
x:x_1\to x_2\\
t:t_1\to t_2
\end{cases}
\end{align}
とします。こういう風に対応する\(t_1\)、\(t_2\)をてきとうに選んできただけです。
微小幅については以下のように考えればいいです。
\frac{dx}{dt}=v(t)\rightarrow dx=v(t)dt
\end{align}
先ほどまでの数学準備の章ではここに意味を感じられなかったかもしれませんが、今回は微小時間間隔\(dt\)の間の質点の変位が\(dx\)だということを意識しておくことも重要です。
もともと被積分関数は\(t\)の関数となっているので、\(x\)の逆関数として\(t\)を解いて云々という作業は今回は不必要ですね。
積分変数を置換した後の形は次のような形になります。
&m\int^{x_2}_{x_1}\dot{v}(t)dx=\int^{x_2}_{x_1}F(t)dx\\
\Longleftrightarrow& m\int^{t_2}_{t_1}\dot{v}(t)v(t)dt=\int^{t_2}_{t_1}F(t)v(t)dt
\end{align}
わざわざの\(x\)積分を\(t\)の積分に直すのと、元からで積分するのでは形が違うこともここまで来たらわかりますね。
もしマキノさんが運動方程式を時間積分した形を覚えていないなら少し前まで戻って復習してください。
先ほどの数学準備の章で準備したテクニックを使うとこの左辺をもう少し変形できます。このような形です。
&m\int^{t_2}_{t_1}\dot{v}(t)v(t)dt\\
=&\int^{t_2}_{t_1}\frac{d}{dt}\left(\frac{v^2(t)}{2}\right)dt\\
=&\frac{mv^2(t_2)}{2}-\frac{mv^2(t_1)}{2}
\end{align}
最初の等号のところの被積分関数の変形が合成関数の微分のテクニックを使っているところです。
ここまでをまとめると、運動方程式を空間積分したものは次のような形にまとまります。
\frac{mv^2(t_2)}{2}-\frac{mv^2(t_1)}{2}=\int^{t_2}_{t_1}F(t)v(t)dt
\end{align}
運動量の章のところを思い出して欲しいのですが、左辺はある値の変化を表していて、右辺はその変化量を表していることは、今回の式も、運動量のところで出た式でも同じです。
今回の式の各項にももちろん名前が付いています。
定義
\frac{mv^2(t_2)}{2}-\frac{mv^2(t_1)}{2}=\int^{t_2}_{t_1}F(t)v(t)dt
\end{align}
左辺第1項を時刻における質点mの運動エネルギー、第2項を時刻における質点mの運動エネルギーという。右辺は時刻からの間に力\(F(t)\)が質点mに与えた仕事という。また、右辺の被積分関数のことを仕事率という。
このようにして、物理にエネルギーという概念が導入されます。
これだけではエネルギーとは何ぞやって思いますよね。実際それで間違ってないです。熱力学などを勉強するともう少しエネルギーの概念がイメージしやすくなるでしょうけど、それまではしばらく問題を「解いては慣れて、慣れてはまた解いて」を繰り返していくしかないです。
先ほどの定義のところで書いた式を改めて見返してみましょう。
まず左辺から。
運動エネルギーというのは、質量が有限で（ゼロではなくて）、速度が有限（ゼロではないもの）であれば、全てのものが所持している物理量です。
質量が2倍になれば、エネルギーも2倍に、速度が2倍になればエネルギーは4倍に、このような関係性だけひとまずインプットしておくことは重要です。
右辺も見てみましょう。
被積分関数を見てみると、「力\(F(t)\)」×「微小変位」になっていることがわかりますね。
力に微小変位をかけて、それを集めてきたものが仕事になると覚えておくといいですね。後で、この辺りももう少し詳しく説明することになります。
問題を解いて少しでもエネルギーの概念に慣れていただきましょう。
問題
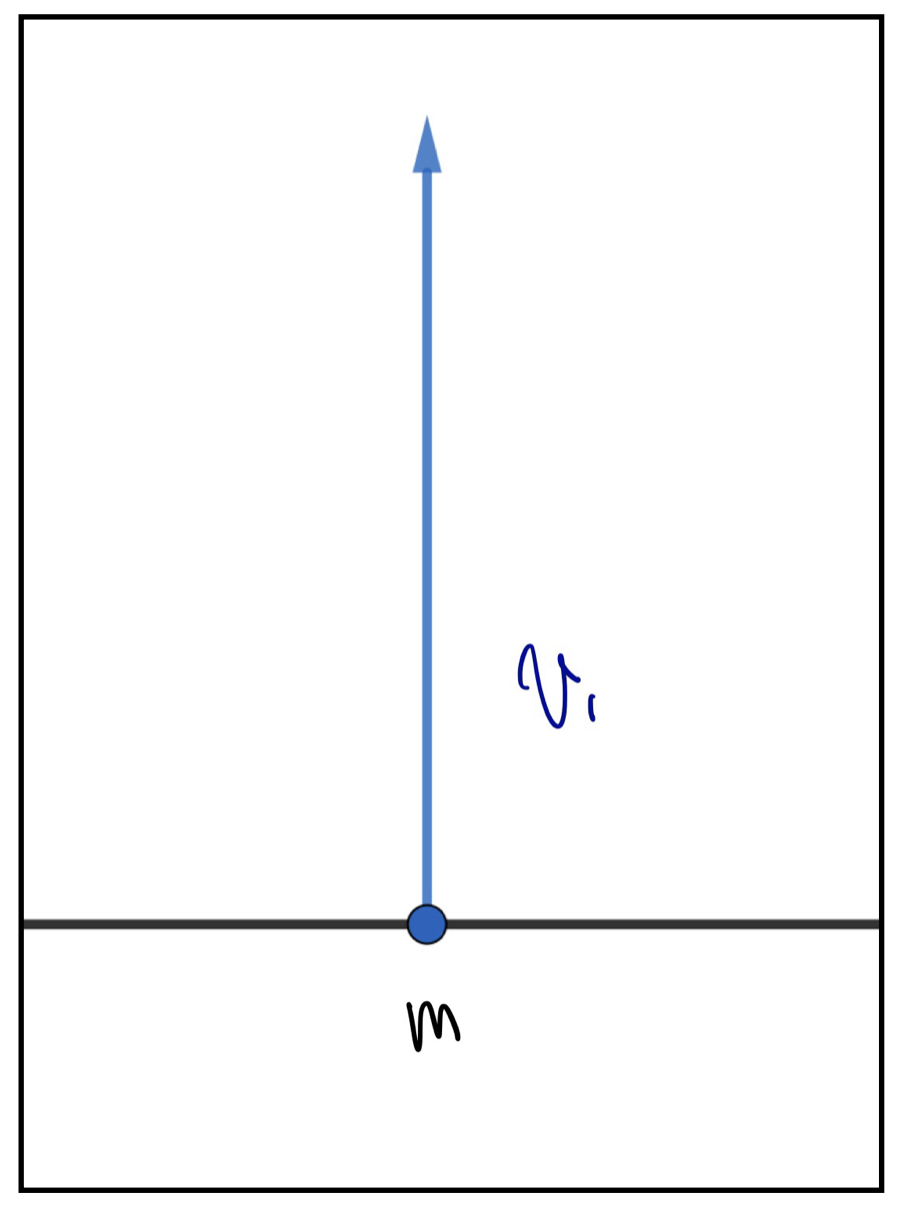
図のように時刻\(t_1\)において、水平面から真上に質点mを速度\(v_1\)で投げ上げた。\(t_1\)以降の任意の時刻\(t_2\)において、質点が持つ運動エネルギーを求めよ。（ただし、\(t_2\)は着地以前とする。）
解答
運動エネルギーの変化は仕事を使って計算することができます。時刻\(t_2\)における質点の速度を\(v_2\)とすると、
\frac{mv_2^2}{2}-\frac{mv_1^2}{2}=\int^{t_2}_{t_1}F(t)v(t)dt
\end{align}
と書けますね。この問題においては、質点にかかる力\(F(t)\)は重力だけですから右辺は以下のように計算できます。（\(mg\)の符号に注意）
&\int^{t_2}_{t_1}F(t)v(t)dt\\
=&-mg\int^{t_2}_{t_1}v(t)dt\\
=&-mg\int^{t_2}_{t_1}\dot{x}(t)dt\\
=&-mgx_2+mgx_1
\end{align}
ここで時刻に\(t_2\)おける質点mの水平面からの位置を\(x_2\)、\(t_1\)においては\(x_1\)としました。これを元の式に代入して整理すると、時刻\(t_2\)での質点mの運動エネルギーが次のようになることがわかります。
\frac{mv_2^2}{2}=\frac{mv_1^2}{2}+mgx_1-mgx_2
\end{align}
関連リンク
>>YouTubeで使用可能な数学と物理の参考書「アラサー高校物理」
東大理系攻略法を
解説したPDF販売中！
中高一貫校に行かなくても、塾に行かなくても、独学で受かるための勉強法を完全解説！
全科目の参考書
全参考書の使い方
受験までの勉強スケジュール
が全てわかります！
今だけ！100様限定60%OFF！
さらに24時間以内なら返金保証つき！
無料サンプル公開！
